8 5 Proving Triangles are Similar Geometry Ms

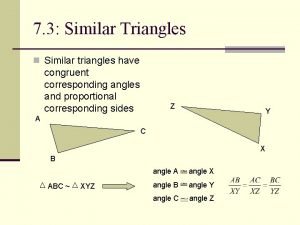
8. 5 Proving Triangles are Similar Geometry Ms. Shum

Objectives: • Use similarity theorems to prove that two triangles are similar • Use similar triangles to solve reallife problems such as finding the height of a climbing wall.

Using Similarity Theorems • In this lesson, you will study 2 alternate ways of proving that two triangles are similar: Side-Side Similarity Theorem and the Side-Angle-Side Similarity Theorem.

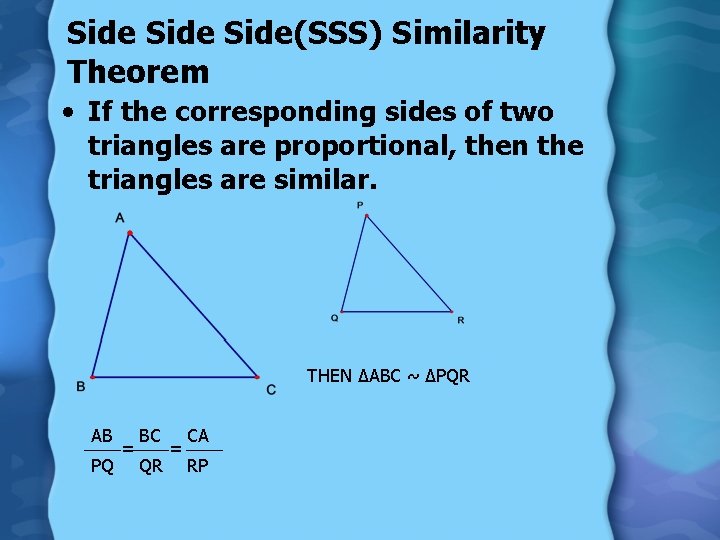
Side(SSS) Similarity Theorem • If the corresponding sides of two triangles are proportional, then the triangles are similar. THEN ∆ABC ~ ∆PQR AB PQ = BC QR = CA RP

Side Angle Side Similarity Thm. • If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar. If X M and THEN ∆XYZ ~ ∆MNP ZX PM = XY MN

Ex. 1: Proof of Theorem 8. 2 • Given: RS LM = • Prove ST MN = TR ∆RST ~ ∆LMN NL Locate P on RS so that PS = LM. Draw PQ so that PQ ║ RT. Then ∆RST ~ ∆PSQ, by the AA Similarity Postulate, and RS LM = ST MN = TR NL Because PS = LM, you can substitute in the given proportion and find that SQ = MN and QP = NL. By the SSS Congruence Theorem, it follows that ∆PSQ ∆LMN Finally, use the definition of congruent triangles and the AA Similarity Postulate to conclude that ∆RST ~ ∆LMN.

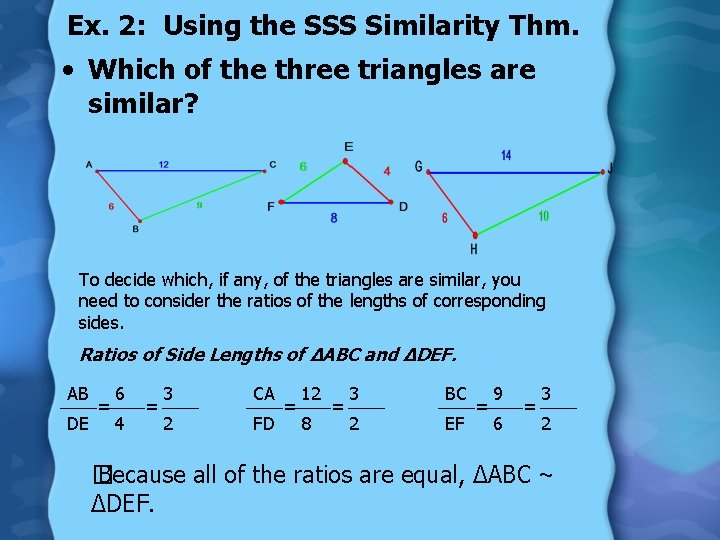
Ex. 2: Using the SSS Similarity Thm. • Which of the three triangles are similar? To decide which, if any, of the triangles are similar, you need to consider the ratios of the lengths of corresponding sides. Ratios of Side Lengths of ∆ABC and ∆DEF. AB DE = 6 4 = 3 CA 2 FD = 12 8 = 3 BC 2 EF = 9 6 = 3 2 � Because all of the ratios are equal, ∆ABC ~ ∆DEF.

Ratios of Side Lengths of ∆ABC ~ ∆GHJ AB GH = 6 6 =1 CA JG = 12 14 = 6 BC 7 HJ = 9 10 � Because the ratios are not equal, ∆ABC and ∆GHJ are not similar. Since ∆ABC is similar to ∆DEF and ∆ABC is not similar to ∆GHJ, ∆DEF is not similar to ∆GHJ.

Ex. 3: Using the SAS Similarity Thm. • Use the given lengths to prove that ∆RST ~ ∆PSQ. Given: SP=4, PR = 12, SQ = 5, and QT = 15; Prove: ∆RST ~ ∆PSQ Use the SAS Similarity Theorem. Begin by finding the ratios of the lengths of the corresponding sides. SR SP + PR 4 + 12 16 = = = SP SP 4 4 = 4

ST SQ + QT 5 + 15 20 = = = SQ SQ 5 5 = 4 So, the side lengths SR and ST are proportional to the corresponding side lengths of ∆PSQ. Because S is the included angle in both triangles, use the SAS Similarity Theorem to conclude that ∆RST ~ ∆PSQ.

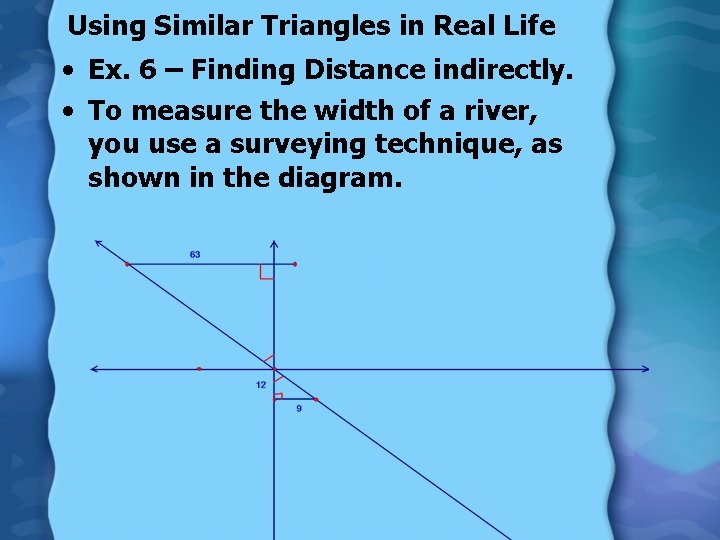
Using Similar Triangles in Real Life • Ex. 6 – Finding Distance indirectly. • To measure the width of a river, you use a surveying technique, as shown in the diagram.

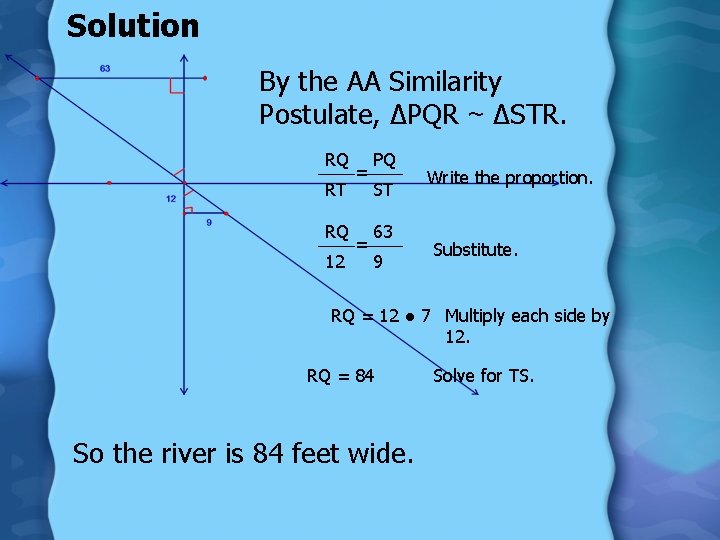
Solution By the AA Similarity Postulate, ∆PQR ~ ∆STR. RQ RT RQ 12 = = PQ ST 63 9 Write the proportion. Substitute. RQ = 12 ● 7 Multiply each side by 12. RQ = 84 So the river is 84 feet wide. Solve for TS.