8 4 A Logarithmic and Exponential Equations Write

8. 4 A Logarithmic and Exponential Equations Write in logarithmic form Write in exponential form Math 30 -1 1

Strategy One: Exponents When solving a logarithmic equation, try rewriting the equation in exponential form. Rewrite the problem in exponential form. Math 30 -1 2

Strategy Two: Equating Logarithms Property of Equality for Logarithmic Equations. For equations with logarithmic expressions on both sides the equal sign, if the bases match, then the arguments must be equal. Restrictions Math 30 -1 3

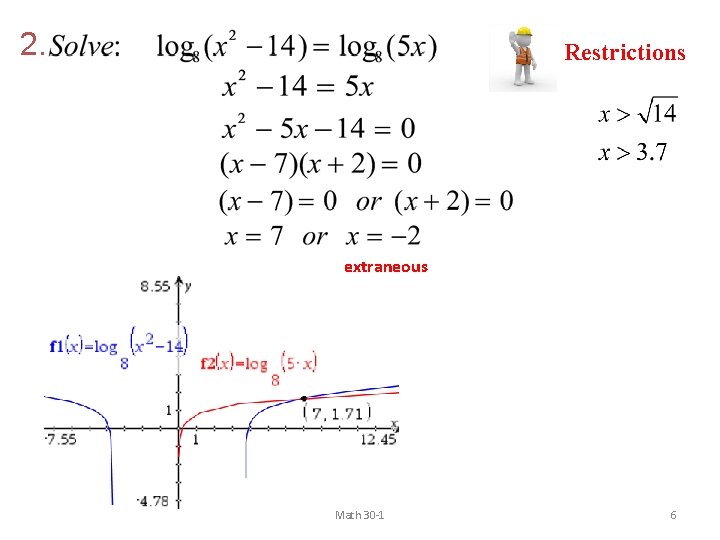
Strategy Three: Graphically. Restrictions Since the bases are both ‘ 3’ we set the arguments equal. extraneous No solution Math 30 -1 4

Solving Log Equations 1. log 272 = log 2 x + log 212 log 272 - log 212 = log 2 x Restrictions x=6 Math 30 -1 5

2. Restrictions extraneous Math 30 -1 6

Solving Log Equations 3. log 7(2 x + 2) - log 7(x - 1) = log 7(x + 1) Verify Algebraically: Restrictions 2 x + 2 = (x- 1)(x + 1) 2 x + 2 = x 2 - 1 0 = x 2 - 2 x - 3 0 = (x - 3)(x + 1) x - 3 = 0 or x + 1 = 0 x=3 x = -1 Therefore, x = 3 extraneous log 7(2 x + 2) - log 7(x - 1) = log 7(x + 1) log 7(2(3) + 2) - log 7(3 - 1) = log 7(3 + 1) log 7(2(-1) + 2) - log 7(-1 - 1) = log 7(-1 + 1) log 70 - log 7(-2) = log 7(0) log 74 = log 74 Math 30 -1 Negative logarithms and logs of 0 are undefined. 7

Solving Log Equations Restrictions 4. log 7(x + 1) + log 7(x - 5) = 1 log 7[(x + 1)(x - 5)] = log 77 (x + 1)(x - 5) = 7 x 2 - 4 x - 5 = 7 x 2 - 4 x - 12 = 0 (x - 6)(x + 2) = 0 x - 6 = 0 or x + 2 = 0 x=6 x = -2 x=6 extraneous Math 30 -1 8

Solving Exponential Equations Unlike Bases 5. 6. Solve for x: 2 x = 8 log 2 x = log 8 xlog 2 = log 12 x=3 x = 3. 58 23. 58 = 12 Math 30 -1 9

Solving Log Equations 7. 8. Solve log 5(x - 6) = 1 - log 5(x - 2) xlog 7 = 2 log 40 x = 3. 79 log 5(x - 6) + log 5(x - 2) = 1 log 5(x - 6)(x - 2) = log 551 (x - 6)(x - 2) = 5 x 2 - 8 x + 12 = 5 x 2 - 8 x + 7 = 0 (x - 7)(x - 1) = 0 x = 7 or x = 1 Since x > 6, the value of x = 1 is extraneous therefore, the solution is x = 7. Math 30 -1 10

Solving Log Equations 10. 2(18)x = 6 x + 1 3 x = 2 x + 1 log[2(18)x] = log(6 x + 1) log(3 x) = log(2 x + 1) log 2 + x log 18 = (x + 1)log 6 x log 3 = (x + 1)log 2 x log 3 = x log 2 + 1 log 2 + x log 18 = x log 6 + 1 log 6 x log 18 - x log 6 = log 6 - log 2 x log 3 - x log 2 = log 2 x(log 18 - log 6) = log 6 - log 2 x(log 3 - log 2) = log 2 9. x = 1. 71 x =1 Math 30 -1 11

Assignment Page 412 1, 2, 3, 4 b, c, 5 a, c, 6, 7 c, d, 8, 18 Math 30 -1 12