8 3 MULTIPLYING BINOMIALS Distributive Property for any

8. 3 MULTIPLYING BINOMIALS: Distributive Property: for any real numbers a, b, c, and d: (a+b)(c+d)= ac+ad+bc +bd

8. 3 MULTIPLYING BINOMIALS: FOIL METHOD: for any real numbers a, b, c, and d in (a+b)(c+d): FIRST: (a)(c) = ac OUTER: (a)(d) = ad INNER: (b)(c) = bc LAST: (b)(d) = bd = ac+ad+bc+bd

GOAL:

MULTIPLYING BINOMIALS: When multiplying polynomials we must keep in mind the laws of exponents from chapter 7 and the distributive property. Ex: What is the simplest form of: (2 x+4)(3 x– 7)?

FOIL METHOD: (2 x+4)(3 x– 7)? FIRST: (2 x)(3 x) = 6 x 2 OUTER: (2 x)(-7) = -14 x INNER: (4)(3 x) = 12 x LAST: (4)(-7) = -28 2 6 x -14 x+12 x-28 6 x 2 -2 x-28 The simplest form is: 6 x 2 -2 x-28

MULTIPLYING BINOMIALS: We can also use a table to: 3 x -7 2 x 4 2 6 x 12 x -14 x -28 2 6 x +12 x-14 x-28 2 6 x -2 x-28

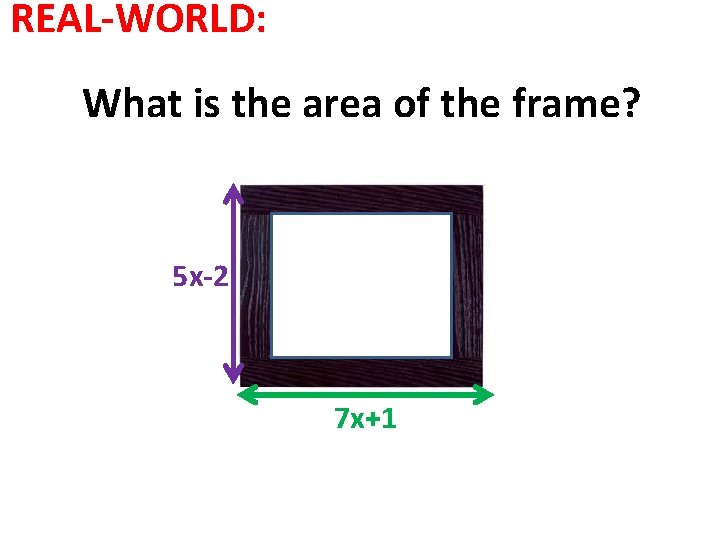
REAL-WORLD: What is the area of the frame? 5 x-2 7 x+1

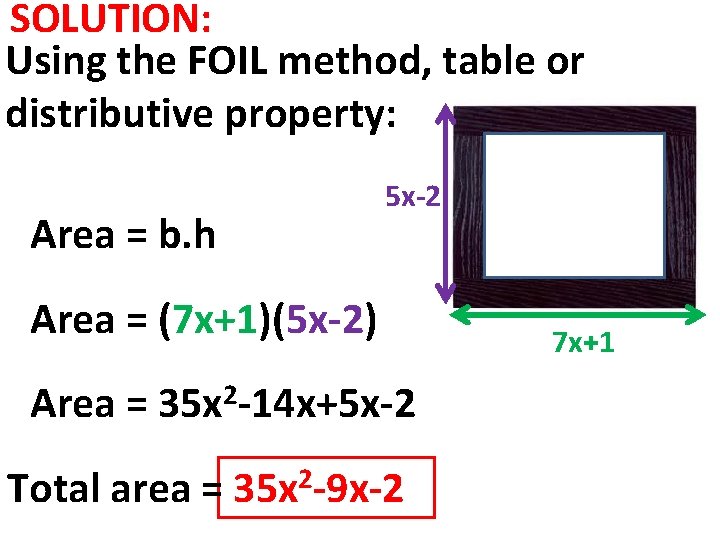
SOLUTION: Using the FOIL method, table or distributive property: Area = b. h 5 x-2 Area = (7 x+1)(5 x-2) Area = 2 35 x -14 x+5 x-2 Total area = 35 x 2 -9 x-2 7 x+1

REAL-WORLD: A factory is looking into making the new label of a can of soup. The can needs to have the dimensions shown in the sketch. what is the total amount of paper needed to make a label?

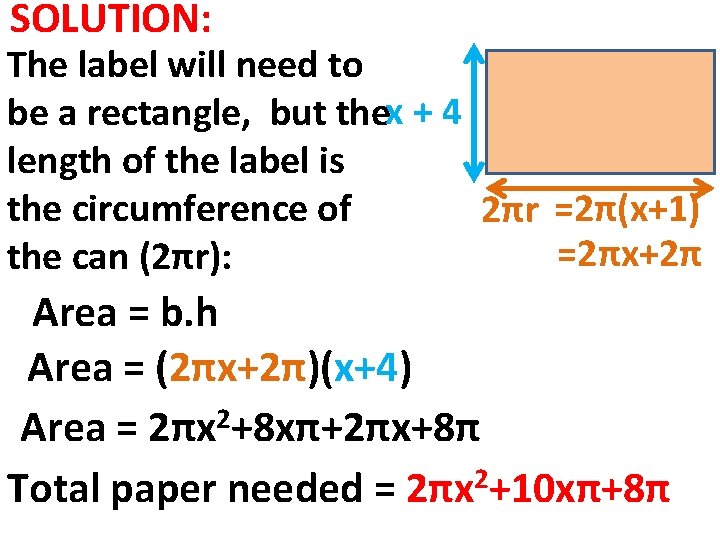
SOLUTION: The label will need to be a rectangle, but thex + 4 length of the label is the circumference of 2πr =2π(x+1) =2πx+2π the can (2πr): Area = b. h Area = (2πx+2π)(x+4) Area = 2πx 2+8 xπ+2πx+8π Total paper needed = 2πx 2+10 xπ+8π

VIDEOS: Polynomials Multiplying: https: //www. khanacademy. org/math/trigonometry/poly nomial_and_rational/polynomial_tutorial/v/multiplyingpolynomials

CLASSWORK: Page 489 -490: Problems: As many as needed to master the concept