8 3 Measures of Dispersion Compute the range

  • Slides: 15
Download presentation
8. 3 Measures of Dispersion • Compute the range of a data set. •

8. 3 Measures of Dispersion • Compute the range of a data set. • Understand how the standard deviation measures the spread of a distribution. • Use the coefficient of variation to compare the standard deviations of different distributions.

The Range of a Data Set © 2010 Pearson Education, Inc. All rights reserved.

The Range of a Data Set © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 2

The Range of a Data Set • Example: Find the range of the heights

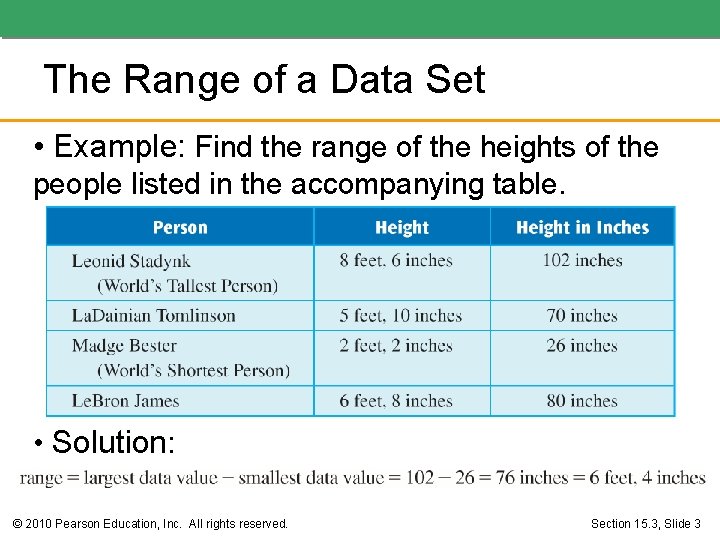
The Range of a Data Set • Example: Find the range of the heights of the people listed in the accompanying table. • Solution: © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 3

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 4

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 5

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 6

Standard Deviation • Example: A company has hired six interns. After 4 months, their

Standard Deviation • Example: A company has hired six interns. After 4 months, their work records show the following number of work days missed for each worker: 0, 2, 1, 4, 2, 3 Find the standard deviation of this data set. • Solution: Mean: (continued on next slide) © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 7

Standard Deviation We calculate the squares of the deviations of the data values from

Standard Deviation We calculate the squares of the deviations of the data values from the mean. Standard Deviation: © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 8

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide

Standard Deviation © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 9

Standard Deviation • Example: The following are the closing prices for a stock for

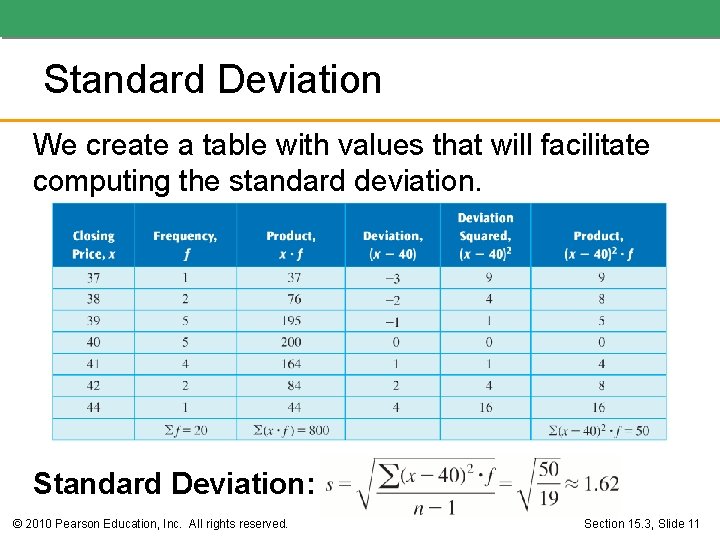
Standard Deviation • Example: The following are the closing prices for a stock for the past 20 trading sessions: 37, 39, 40, 38, 39, 40, 41, 39, 41, 42, 44, 39, 40, 41 What is the standard deviation for this data set? • Solution: Mean: (sum of the closing prices is 800) (continued on next slide) © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 10

Standard Deviation We create a table with values that will facilitate computing the standard

Standard Deviation We create a table with values that will facilitate computing the standard deviation. Standard Deviation: © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 11

Standard Deviation Comparing Standard Deviations All three distributions have a mean and median of

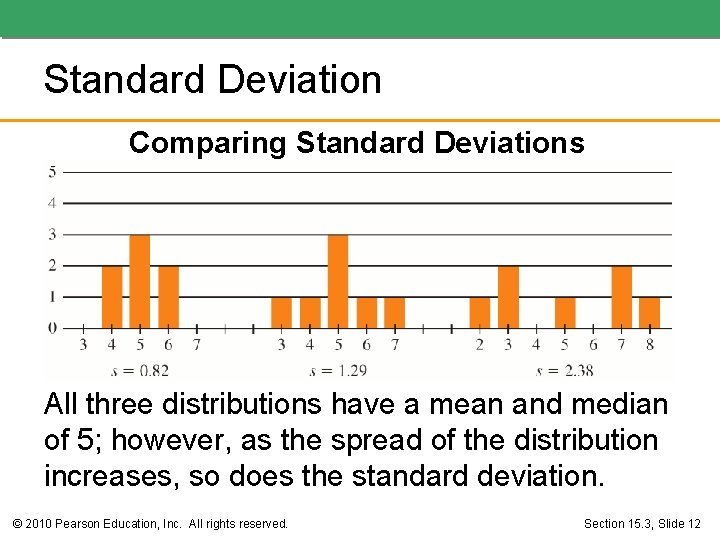
Standard Deviation Comparing Standard Deviations All three distributions have a mean and median of 5; however, as the spread of the distribution increases, so does the standard deviation. © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 12

The Coefficient of Variation Relatively speaking there is more variation in the weights of

The Coefficient of Variation Relatively speaking there is more variation in the weights of the 1 st graders than the NFL players below. 1 st Graders NFL Players Mean: 30 pounds Mean: 300 pounds SD: 3 pounds SD: 10 pounds CV: © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 13

The Coefficient of Variation • Example: Use the coefficient of variation to determine whether

The Coefficient of Variation • Example: Use the coefficient of variation to determine whether the women’s 100 -meter race or the men’s marathon has had more consistent times over the five Olympics listed. (continued on next slide) © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 14

The Coefficient of Variation • Solution: 100 Meters Marathon Mean: 10. 796 Mean: 7,

The Coefficient of Variation • Solution: 100 Meters Marathon Mean: 10. 796 Mean: 7, 891. 4 SD: 0. 163 SD: 83. 5 CV: Using the coefficient of variation as a measure, there is less variation in the times for the marathon than for the 100 -meter race. © 2010 Pearson Education, Inc. All rights reserved. Section 15. 3, Slide 15