8 3 Counting Apply the fundamental counting principle

  • Slides: 25
Download presentation
8. 3 Counting • Apply the fundamental counting principle • Calculate and apply permutations

8. 3 Counting • Apply the fundamental counting principle • Calculate and apply permutations • Calculate and apply combinations Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Tree Diagram (1 of 2) Suppose that a quiz has only two questions. The

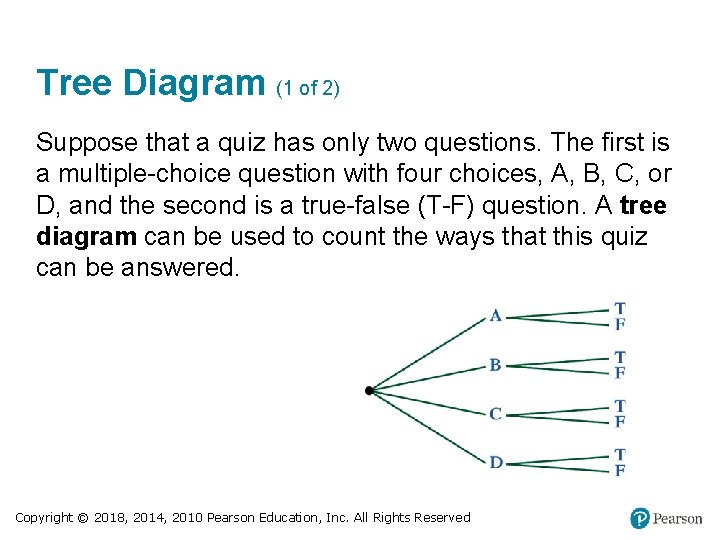
Tree Diagram (1 of 2) Suppose that a quiz has only two questions. The first is a multiple-choice question with four choices, A, B, C, or D, and the second is a true-false (T-F) question. A tree diagram can be used to count the ways that this quiz can be answered. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Tree Diagram (2 of 2) A tree diagram is a systematic way of listing

Tree Diagram (2 of 2) A tree diagram is a systematic way of listing every possibility. We can see that there are eight ways to answer the test. They are AT, AF, BT, BF, CT, CF, DT, and DF. For instance, CF indicates a quiz with answers of C on the first question and F on the second question. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Fundamental Counting Principle Let E 1, E 2, E 3, …, En be a

Fundamental Counting Principle Let E 1, E 2, E 3, …, En be a sequence of n independent events. If event Ek can occur mk ways for k = 1, 2, 3, …, n, then there are m 1 • m 2 • m 3 • … • mn ways for all n events to occur. Two events are independent if neither event influences the outcome of the other. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting ways to answer an exam (1 of 2) An exam contains four

Example: Counting ways to answer an exam (1 of 2) An exam contains four true-false questions and six multiple-choice questions. Each multiple-choice question has five possible answers. Count the number of ways that the exam can be answered. Solution This is a sequence of 10 independent events. There are two ways to answer each of the first four questions. There are five ways to answer the next 6 questions. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting ways to answer an exam (2 of 2) The number of ways

Example: Counting ways to answer an exam (2 of 2) The number of ways to answer the exam is Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting license plates (1 of 2) Sometimes a license plate is limited to

Example: Counting license plates (1 of 2) Sometimes a license plate is limited to 3 uppercase letters (A through Z) followed by 3 digits (0 through 9). For example, ABB 112 would be a valid license plate. Would this format provide enough license plates for a state with 8 million vehicles? Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting license plates (2 of 2) Solution 26 choices for letters 10 choices

Example: Counting license plates (2 of 2) Solution 26 choices for letters 10 choices for digits There are 26 ways to choose each of the three letters and 10 ways to choose each of the 3 digits. This format for license plates could accommodate more than 8 million vehicles. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting toll-free telephone numbers (1 of 2) Count the total number of 800

Example: Counting toll-free telephone numbers (1 of 2) Count the total number of 800 numbers if the local portion of a telephone number (the last seven digits) does not start with a 0 or 1. Solution A toll-free 800 number assumes the following form. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting toll-free telephone numbers (2 of 2) We can think of choosing the

Example: Counting toll-free telephone numbers (2 of 2) We can think of choosing the remaining digits for the local number as seven independent events. Since the local number cannot begin with a 0 or 1, there are eight possibilities (2 to 9) for the first digit. The remaining six digits can be any number from 0 to 9, so there are ten possibilities for each of these digits. The total is given by Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Permutations A permutation is an ordering or arrangement. For example, suppose that three students

Permutations A permutation is an ordering or arrangement. For example, suppose that three students are scheduled to give speeches in a class. The different arrangements in which these speeches can be ordered are called permutations. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

n-Factorial Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

n-Factorial Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Calculating factorials (1 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc.

Example: Calculating factorials (1 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Calculating factorials (2 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc.

Example: Calculating factorials (2 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Permutations of n Elements Taken r at a Time If P(n, r) denotes the

Permutations of n Elements Taken r at a Time If P(n, r) denotes the number of permutations of n elements taken r at a time, with r ≤ n, then Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Calculating permutations For a class of 30 students, how many arrangements are there

Example: Calculating permutations For a class of 30 students, how many arrangements are there in which 4 students each give a speech? Solution The number of permutations of 30 elements taken 4 at a time is given by There are 657, 720 ways to arrange the four speeches. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Combination (1 of 2) A combination is not an ordering or arrangement, but rather

Combination (1 of 2) A combination is not an ordering or arrangement, but rather a subset of a set of elements. Order is not important when finding combinations. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Combination (2 of 2) For example, suppose we want to select a tennis team

Combination (2 of 2) For example, suppose we want to select a tennis team of two players from four people. The order in which the selection is made does not affect the final team of two players. From a set of four people, we select a subset of two players. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Combinations of n Elements Taken r at a Time If C(n, r) denotes the

Combinations of n Elements Taken r at a Time If C(n, r) denotes the number of combinations of n elements taken r at a time, with r ≤ n, then Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Calculating C(n, r) (1 of 2) Calculate each of the following. Support your

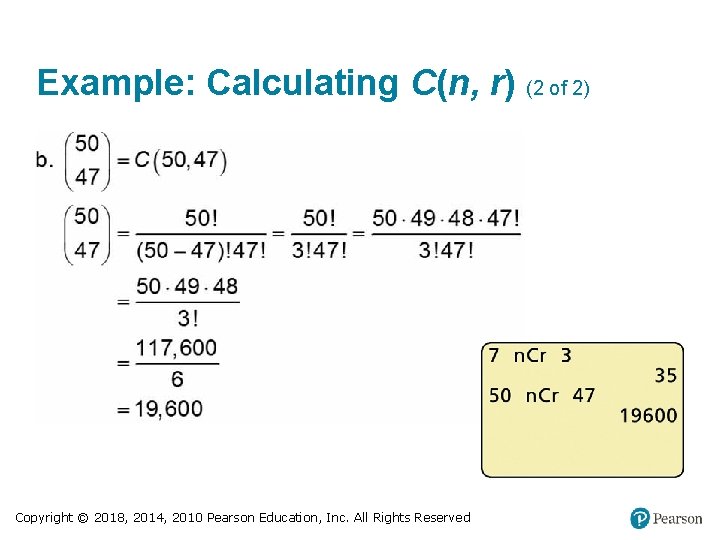
Example: Calculating C(n, r) (1 of 2) Calculate each of the following. Support your answer by using a calculator. Solution Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Calculating C(n, r) (2 of 2) Copyright © 2018, 2014, 2010 Pearson Education,

Example: Calculating C(n, r) (2 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting combinations (1 of 2) A college student has five courses left in

Example: Counting combinations (1 of 2) A college student has five courses left in her major and plans to take two of them this semester. Assuming that this student has the prerequisites for all five courses, determine how many ways these two courses can be selected. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting combinations (2 of 2) Solution The order in which the courses are

Example: Counting combinations (2 of 2) Solution The order in which the courses are selected is unimportant. From a set of 5 courses, the student selects a subset of 2 courses. The number of subsets is There are 10 ways to select two courses from a set of five. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting committees (1 of 2) How many committees of six people can be

Example: Counting committees (1 of 2) How many committees of six people can be selected from six women and three men, if a committee must consist of at least two men? Solution Two Men: Committee would be two men and four women. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Counting committees (2 of 2) Three Men: Committee would be three men and

Example: Counting committees (2 of 2) Three Men: Committee would be three men and three women The total number of possible committees would be 45 + 20 = 65 Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Fundamental Counting Principle Permutations Objectives apply fundamental countingFundamental Counting Principle Permutations Objectives apply fundamental counting
Counting Principle The Fundamental Counting Principle The CountingCounting Principle The Fundamental Counting Principle The Counting
The Fundamental Counting Principle The fundamental counting principleThe Fundamental Counting Principle The fundamental counting principle
Counting Principles Mulitplication Counting Principle Addition Counting PrincipleCounting Principles Mulitplication Counting Principle Addition Counting Principle
Fundamental Counting Theorm Fundamental Counting Principle can beFundamental Counting Theorm Fundamental Counting Principle can be
THE FUNDAMENTAL COUNTING PRINCIPLE PERMUTATIONS THE FUNDAMENTAL COUNTINGTHE FUNDAMENTAL COUNTING PRINCIPLE PERMUTATIONS THE FUNDAMENTAL COUNTING
FUNDAMENTAL COUNTING PRINCIPLE Lesson 9 5 Fundamental CountingFUNDAMENTAL COUNTING PRINCIPLE Lesson 9 5 Fundamental Counting
Permutations and Combinations Objectives apply fundamental counting principlePermutations and Combinations Objectives apply fundamental counting principle
Permutations and Combinations Objectives apply fundamental counting principlePermutations and Combinations Objectives apply fundamental counting principle
Permutations and Combinations Objectives apply fundamental counting principlePermutations and Combinations Objectives apply fundamental counting principle
Basic Counting Principle The Basic Counting Principle WhenBasic Counting Principle The Basic Counting Principle When
Counting Outcomes Day 2 The Fundamental Counting PrincipleCounting Outcomes Day 2 The Fundamental Counting Principle
3 4 Counting Principles Fundamental Counting Principle If3 4 Counting Principles Fundamental Counting Principle If
Section 3 4 Counting Principles Fundamental Counting PrincipleSection 3 4 Counting Principles Fundamental Counting Principle
3 4 Counting Principles Fundamental Counting Principle If3 4 Counting Principles Fundamental Counting Principle If
The Fundamental Counting Principal Permutations The Fundamental CountingThe Fundamental Counting Principal Permutations The Fundamental Counting
Apply the Counting Principle and Permutations Section 10Apply the Counting Principle and Permutations Section 10
Notes 10 1 Apply the Counting Principle andNotes 10 1 Apply the Counting Principle and
SECTION 10 1 1 Apply the Counting PrincipleSECTION 10 1 1 Apply the Counting Principle
Multiplication Principle and Addition Principle 1 Multiplication PrincipleMultiplication Principle and Addition Principle 1 Multiplication Principle
Uncertainty Principle Uncertainly Principle 1 Uncertainty Principle SummaryUncertainty Principle Uncertainly Principle 1 Uncertainty Principle Summary
The Pigeonhole Principle Pigeonhole principle The pigeonhole principleThe Pigeonhole Principle Pigeonhole principle The pigeonhole principle
Chapter 19 Avogadros Principle Avogadros Principle Avogadros PrincipleChapter 19 Avogadros Principle Avogadros Principle Avogadros Principle
PASCALS PRINCIPLE Bernoullis Principle Pascals Principle In thePASCALS PRINCIPLE Bernoullis Principle Pascals Principle In the