8 2 Symmetry Graphing Nonlinear Equations Symmetry yaxis

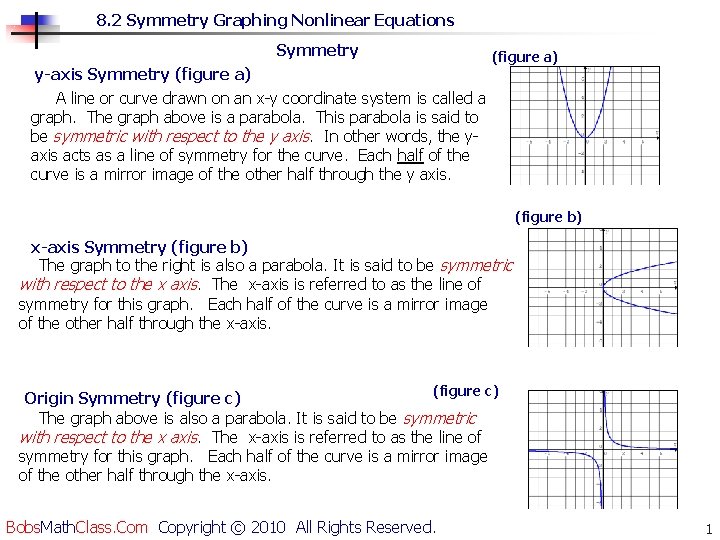
8. 2 Symmetry Graphing Nonlinear Equations Symmetry y-axis Symmetry (figure a) A line or curve drawn on an x-y coordinate system is called a graph. The graph above is a parabola. This parabola is said to be symmetric with respect to the y axis. In other words, the yaxis acts as a line of symmetry for the curve. Each half of the curve is a mirror image of the other half through the y axis. (figure a) (figure b) x-axis Symmetry (figure b) The graph to the right is also a parabola. It is said to be symmetric with respect to the x axis. The x-axis is referred to as the line of symmetry for this graph. Each half of the curve is a mirror image of the other half through the x-axis. (figure c) Origin Symmetry (figure c) The graph above is also a parabola. It is said to be symmetric with respect to the x axis. The x-axis is referred to as the line of symmetry for this graph. Each half of the curve is a mirror image of the other half through the x-axis. Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 1

8. 2 Symmetry Graphing Nonlinear Equations The previous slides were examples of graphs that exhibited some form of symmetry. Not all graphs have symmetry and some may have a combination of symmetries. In our next topic, we will be using algebraic tests on the equations of the graphs to help us determine whether (or not) a graph exhibits one or more of these symmetries. The results of these tests can be used to help us draw the graphs of non-linear equations. Tests for Symmetry (Memorize) Y-Axis Symmetry The graph of an equation is symmetric with respect to the y axis if replacing x with –x results in an equivalent equation. X-Axis Symmetry The graph of an equation is symmetric with respect to the x axis if replacing y with –y results in an equivalent equation. Origin Symmetry The graph of an equation is symmetric with respect to the origin if replacing x with –x and y with –y results in an equivalent equation. Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 2

8. 2 Symmetry Graphing Nonlinear Equations Example 1 a. Determine the point which will be symmetric to (-2, 3) with respect to the y axis. Solution: First graph the point. y axis 5 4 (2, (-2, 3) 3 2 1 Next, find the point symmetric with respect to the y-axis by replacing x with -x. Answer: (2, 3) -6 -5 -4 -3 -2 -1 3) x-axis 1 2 3 4 5 6 -2 -3 -4 1 b. Determine the point which will be symmetric to (-3, 4) with respect to the origin. - (-3, 4) Solution: First graph the point. -5 y axis 5 4 3 2 1 Next, find the point symmetric with respect to the origin by replacing x with –x, and replacing y with -y. -6 -5 -4 -3 -2 -1 1 -2 -3 Answer: (3, -4) - Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. -4 x-axis 2 3 4 5 6 (3, -4) -5 3

8. 2 Symmetry Graphing Nonlinear Equations Your Turn Problem #1 Find the points that are symmetric to (-2, 5) with respect to: Answers a) the x axis a) (-2, -5) b) the y axis b) (2, 5) c) the origin c) (2, -5) Example 2: a) Determine the type(s) of symmetry exhibited by the graph of y = x 2 + 3. 1. Replace x with –x. Does the equation remain the same? 2. Replace y with –y. Does the equation remain the same? 3. Replace x with –x and y with – y. Does the equation remain the same? Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 4

8. 2 Symmetry Graphing Nonlinear Equations Example 2 b) Determine the type(s) of symmetry exhibited by the graph of xy=7 1. Replace x with –x. Does the equation remain the same? 2. Replace y with –y. Does the equation remain the same? 3. Replace x with –x and y with – y. Does the equation remain the same? Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 5

8. 2 Symmetry Graphing Nonlinear Equations – The Parabola Nonlinear equations will be covered more thoroughly in college algebra. For now, we will make use the symmetry information and graph one type of nonlinear equation called a parabola. Basic techniques of graphing is to observe if a graph has symmetry and pick “enough” points to get an accurate sketch of the equation. Next semester, we will cover the parabola and its properties more in depth. Knowing which values to choose for x is important. If we do not choose the “right” values for x, we will not obtain an accurate depiction of the graph. For the next examples and your turn problems, we will pick the following values for x: 0, 1, 2, – 1 , and – 2. Recall the symmetry test. Y-Axis Symmetry The graph of an equation is symmetric with respect to the y axis if replacing x with –x results in an equivalent equation. Next Slide Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 6

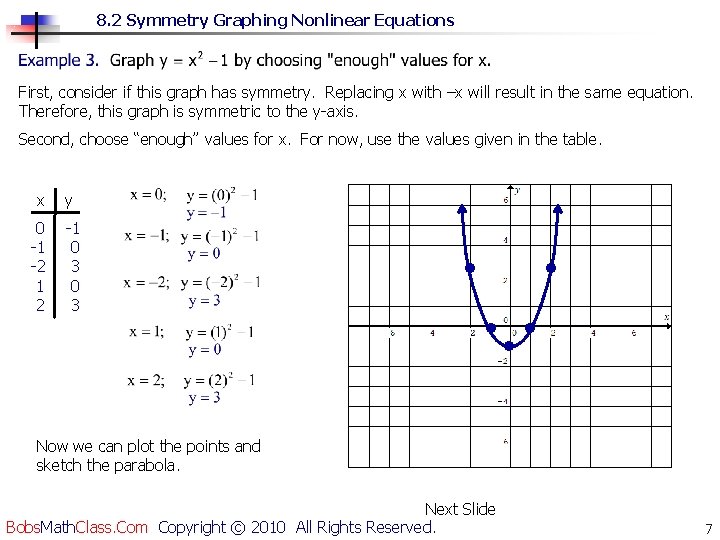
8. 2 Symmetry Graphing Nonlinear Equations First, consider if this graph has symmetry. Replacing x with –x will result in the same equation. Therefore, this graph is symmetric to the y-axis. Second, choose “enough” values for x. For now, use the values given in the table. x y 0 -1 -2 1 2 -1 0 3 • • • Now we can plot the points and sketch the parabola. Next Slide Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 7

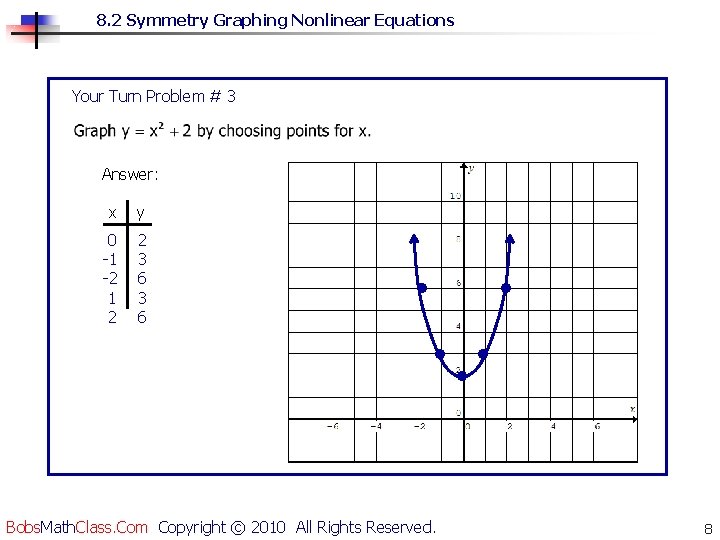
8. 2 Symmetry Graphing Nonlinear Equations Your Turn Problem # 3 Answer: x y 0 -1 -2 1 2 2 3 6 • • • Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. • • 8

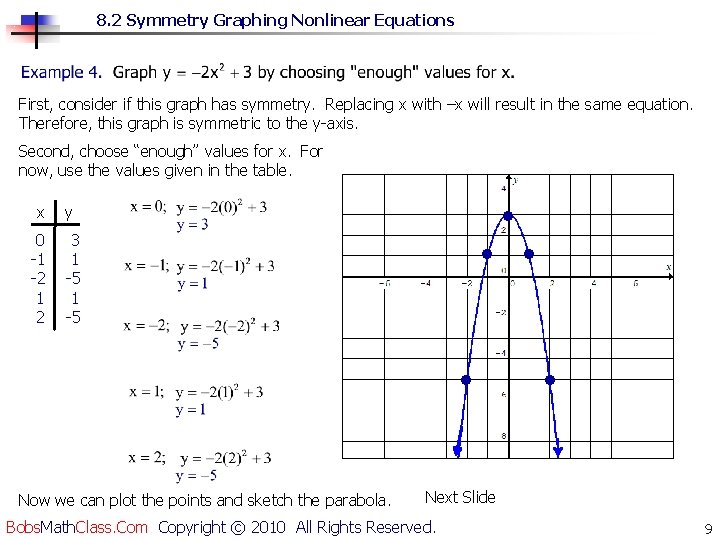
8. 2 Symmetry Graphing Nonlinear Equations First, consider if this graph has symmetry. Replacing x with –x will result in the same equation. Therefore, this graph is symmetric to the y-axis. Second, choose “enough” values for x. For now, use the values given in the table. • Now we can plot the points and sketch the parabola. • 3 1 -5 • 0 -1 -2 1 2 • y • x Next Slide Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. 9

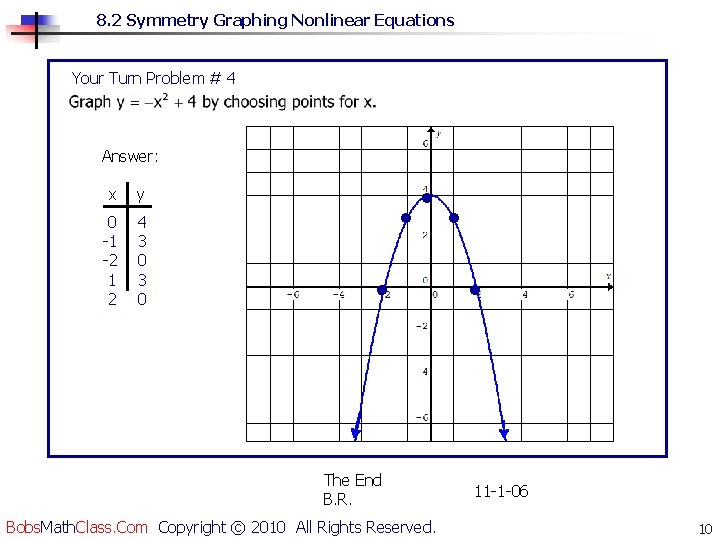
8. 2 Symmetry Graphing Nonlinear Equations Your Turn Problem # 4 Answer: • The End B. R. Bobs. Math. Class. Com Copyright © 2010 All Rights Reserved. • 4 3 0 • 0 -1 -2 1 2 • y • x 11 -1 -06 10