8 1 Ratio and Proportions Ratio a ratio









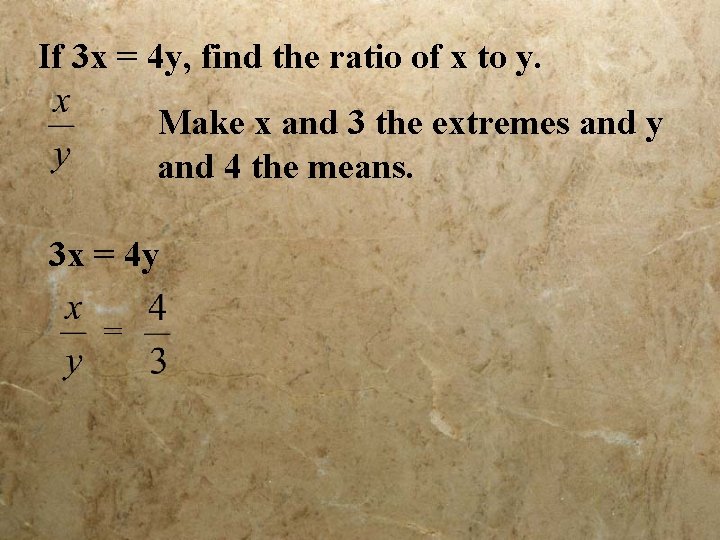
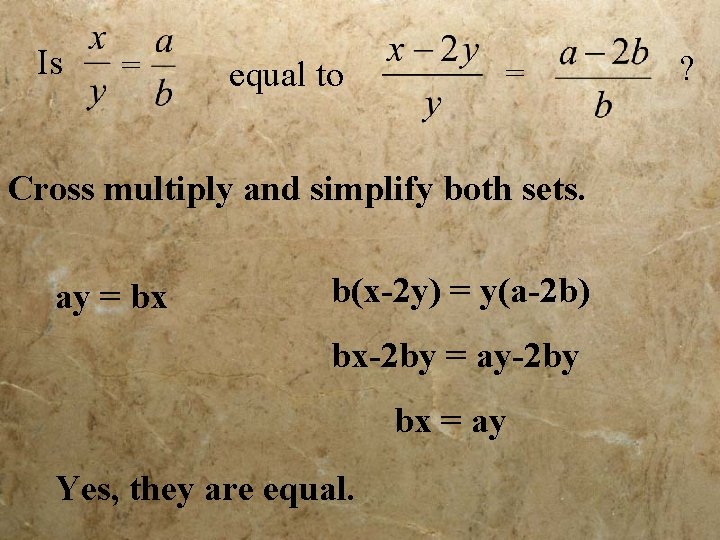
- Slides: 11

8. 1 Ratio and Proportions Ratio: a ratio is a quotient of two numbers. a: b a to b a÷b Always given in lowest terms. Slope of a line is a ratio between two points. (rise over run)

Proportions: two or more ratios set equal to each other. = a is the first term b is the second term c is the third term d is the fourth term a: b = c: d

Product and Ratio Theorems In a product containing four terms: First and fourth terms are the extremes. Second and third terms are the means. T 59: In a proportion, the product of the means is equal to the product of the extremes. (means-extremes product theorem. )

= ad = bc If they aren’t equal, then the ratios aren’t in proportion. T 60: If the product of a pair of non-zero numbers is equal to the product of another pair of non-zero numbers, then either pair of numbers may be made the extremes, and the other pair the means, of a proportion. (means-extremes ratio theorem. )

This theorem is harder to state than to use! Given: pq = rs Then: = pq = rs = = pq = rs These proportions are all equivalent since their cross products are equivalent equations.

In a mean proportion, the means are the same. = 4 is the geometric mean = x is the geometric mean

Definition: If the means in a proportion are equal, either mean is called a geometric mean or mean proportional between the extremes. Arithmetic mean: Geometric mean: = = 15 x 2 = 81 x= 9

Solve: = 7 x = 42 x=6 = 2 x = 12 x=6 You might want to reduce the fraction first.

Find the mean proportional(s) between 4 and 16. = x 2 = 64 x= 8 If we are looking for the length of a segment, then only the positive number works.
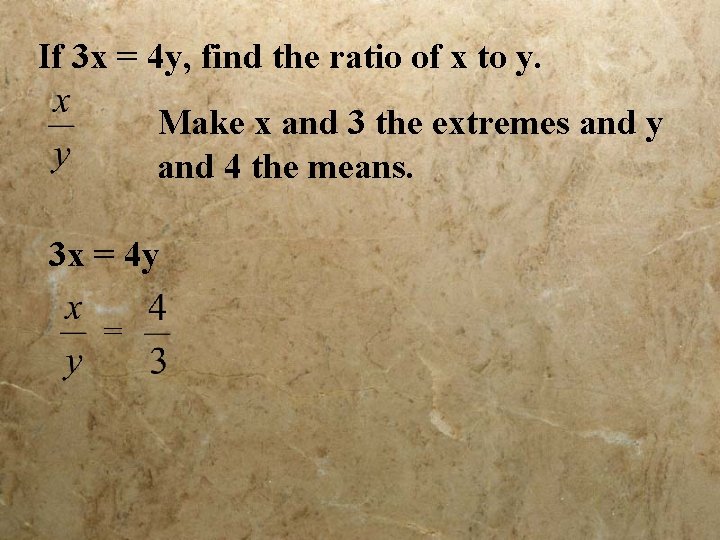
If 3 x = 4 y, find the ratio of x to y. Make x and 3 the extremes and y and 4 the means. 3 x = 4 y =
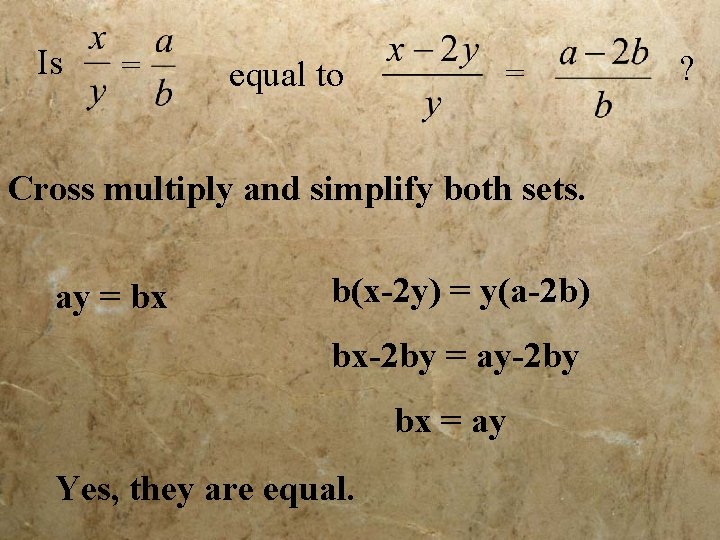
Is = equal to = Cross multiply and simplify both sets. ay = bx b(x-2 y) = y(a-2 b) bx-2 by = ay-2 by bx = ay Yes, they are equal. ?
 8-1 ratios and proportions
8-1 ratios and proportions Ratios, rates, and proportions
Ratios, rates, and proportions 3-2-1 dough refers to what ratio
3-2-1 dough refers to what ratio Core focus on proportions and probability answer key
Core focus on proportions and probability answer key Example of definite composition
Example of definite composition 7-1 ratios and proportions
7-1 ratios and proportions State law of definite proportion
State law of definite proportion Chapter 7 similarity
Chapter 7 similarity Similarity and proportions
Similarity and proportions Chapter 15 furniture styles and construction answer key
Chapter 15 furniture styles and construction answer key 7-1 ratios and proportions
7-1 ratios and proportions Lesson quiz 4-2
Lesson quiz 4-2