7 Trigonometric Identities and Equations Sections 7 5














































- Slides: 60

7 Trigonometric Identities and Equations Sections 7. 5– 7. 7 © 2008 Pearson Addison-Wesley. All rights reserved

7 Trigonometric Identities and Equations 7. 5 Inverse Circular Functions 7. 6 Trigonometric Equations 7. 7 Equations Involving Inverse Trigonometric Functions 54 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Inverse Circular Functions Inverse Functions ▪ Inverse Sine Function ▪ Inverse Cosine Function ▪ Inverse Tangent Function ▪ Remaining Inverse Circular Functions ▪ Inverse Function Values 55 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

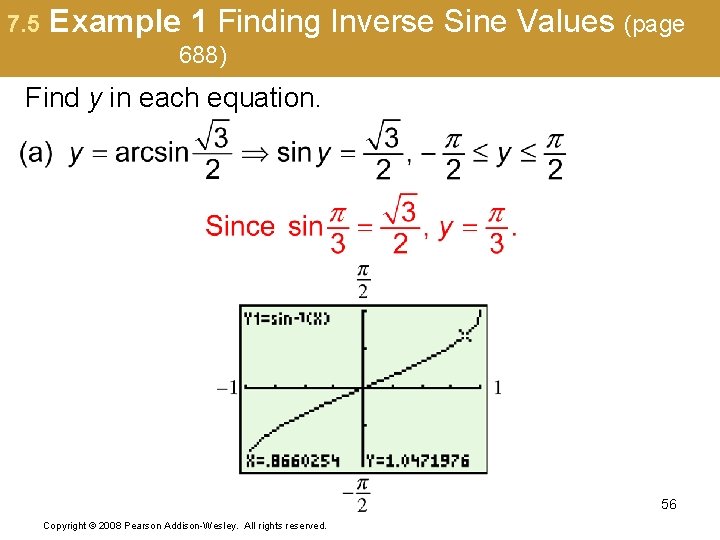
7. 5 Example 1 Finding Inverse Sine Values (page 688) Find y in each equation. 56 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 1 Finding Inverse Sine Values (cont. ) 57 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 1 Finding Inverse Sine Values (cont. ) is not in the domain of the inverse sine function, [– 1, 1], so does not exist. A graphing calculator will give an error message for this input. 58 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

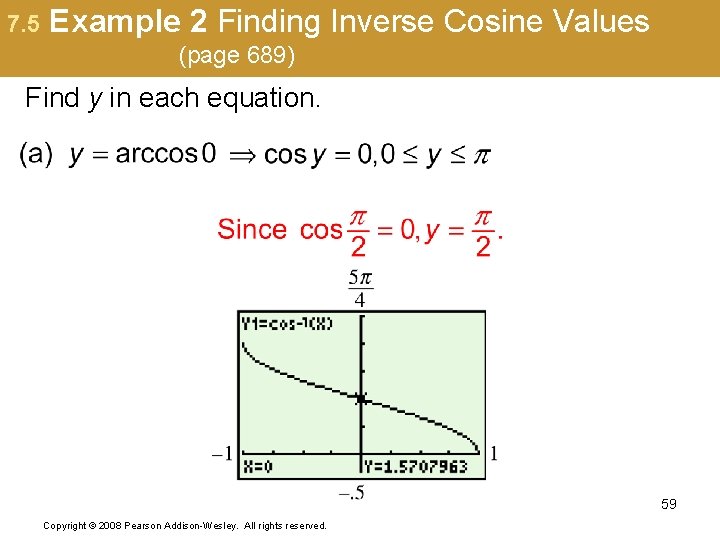
7. 5 Example 2 Finding Inverse Cosine Values (page 689) Find y in each equation. 59 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

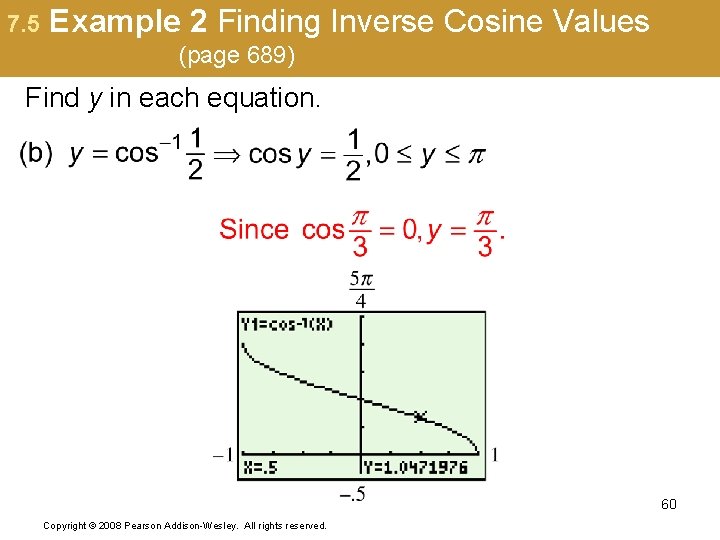
7. 5 Example 2 Finding Inverse Cosine Values (page 689) Find y in each equation. 60 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 3 Finding Inverse Function Values (Degree-Measured Angles) (page 692) Find the degree measure of θ in each of the following. 61 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 4 Finding Inverse Function Values With a Calculator (page 693) (a) Find y in radians if With the calculator in radian mode, enter y = 1. 823476582 Copyright © 2008 Pearson Addison-Wesley. All rights reserved. as 62

7. 5 Example 4(b) Finding Inverse Function Values With a Calculator (page 693) (b) Find θ in degrees if θ = arccot(–. 2528). A calculator gives the inverse cotangent value of a negative number as a quadrant IV angle. The restriction on the range of arccotangent implies that the angle must be in quadrant II, so, with the calculator in degree mode, enter arccot(–. 2528) as 63 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 4(b) Finding Inverse Function Values With a Calculator (cont. ) θ = 104. 1871349° 64 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 5 Finding Function Values Using Definitions of the Trigonometric Functions (page 693) Evaluate each expression without a calculator. Since arcsin is defined only in quadrants I and IV, and is positive, θ is in quadrant I. 65 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 5(a) Finding Function Values Using Definitions of the Trigonometric Functions (cont. ) 66 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 5(b) Finding Function Values Using Definitions of the Trigonometric Functions (page 693) Since arccot is defined only in quadrants I and II, and is negative, θ is in quadrant II. 67 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 5(b) Finding Function Values Using Definitions of the Trigonometric Functions (cont. ) 68 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

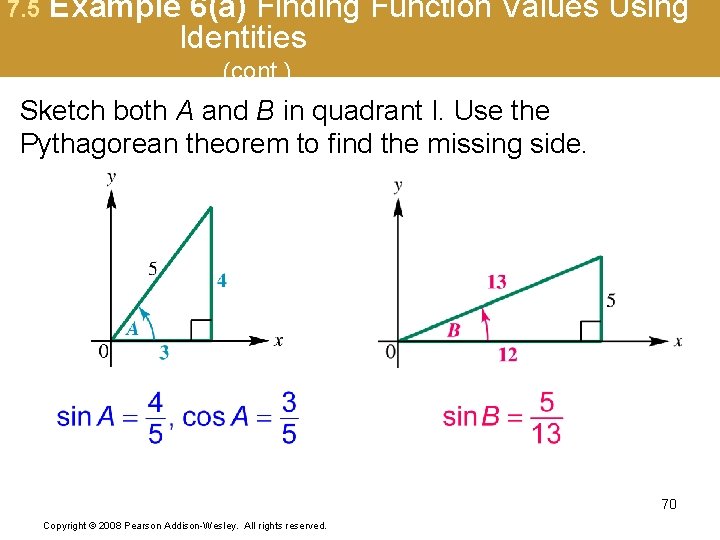
7. 5 Example 6(a) Finding Function Values Using Identities (page 694) Evaluate the expression without a calculator. Use the cosine difference identity: 69 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 6(a) Finding Function Values Using Identities (cont. ) Sketch both A and B in quadrant I. Use the Pythagorean theorem to find the missing side. 70 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 6(a) Finding Function Values Using Identities (cont. ) 71 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 6(b) Finding Function Values Using Identities (page 694) Evaluate the expression without a calculator. sin(2 arccot (– 5)) Let A = arccot (– 5), so cot A = – 5. Use the double-angle sine identity: 72 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 6(b) Finding Function Values Using Identities (cont. ) Sketch A in quadrant II. Use the Pythagorean theorem to find the missing side. 73 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 6(b) Finding Function Values Using Identities (cont. ) 74 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 7(a) Finding Function Values in Terms of u (page 695) Write in u. , as an algebraic expression Sketch θ in quadrant I. Use the Pythagorean theorem to find the missing side. 75 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 7(a) Finding Function Values in Terms of u (cont. ) 76 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 7(b) Finding Function Values in Terms of u (page 695) Write in u. , u > 0, as an algebraic expression Sketch θ in quadrant I. Use the Pythagorean theorem to find the missing side. 77 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 7(b) Finding Function Values in Terms of u (cont. ) Use the double-angle sine identity to find sin 2θ. 78 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

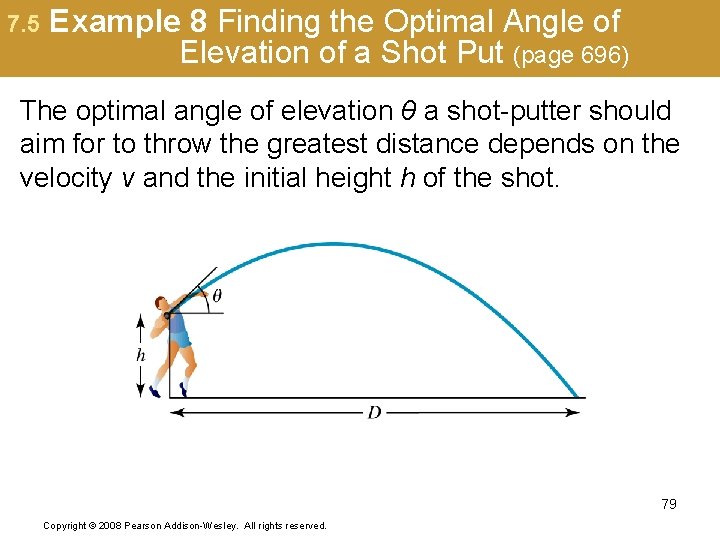
7. 5 Example 8 Finding the Optimal Angle of Elevation of a Shot Put (page 696) The optimal angle of elevation θ a shot-putter should aim for to throw the greatest distance depends on the velocity v and the initial height h of the shot. 79 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 5 Example 8 Finding the Optimal Angle of Elevation of a Shot Put (cont. ) One model for θ that achieves this greatest distance is Suppose a shot-putter can consistently throw the steel ball with h = 7. 5 ft and v = 50 ft per sec. At what angle should he throw the ball to maximize distance? 80 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Trigonometric Equations Solving by Linear Methods ▪ Solving by Factoring ▪ Solving by Quadratic Methods ▪ Solving by Using Trigonometric Identities ▪ Equations with Half-Angles ▪ Equations with Multiple Angles ▪ Applications 81 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

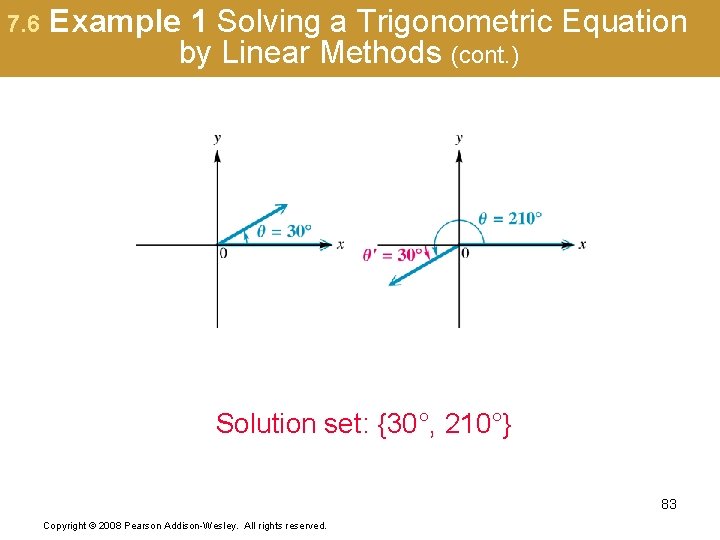
7. 6 Example 1 Solving a Trigonometric Equation by Linear Methods (page 701) is positive in quadrants I and III. The reference angle is 30° because 82 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 1 Solving a Trigonometric Equation by Linear Methods (cont. ) Solution set: {30°, 210°} 83 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 2 Solving a Trigonometric Equation by Factoring (page 701) or Solution set: {90°, 135°, 270°, 315°} 84 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 3 Solving a Trigonometric Equation by Factoring (page 702) 85 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 3 Solving a Trigonometric Equation by Factoring (cont. ) has two solutions, the angles in quadrants III and IV with the reference angle. 729728: 3. 8713 and 5. 5535. has one solution, 86 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 4 Solving a Trigonometric Equation Using the Quadratic Formula (page 702) Find all solutions of Use the quadratic formula with a = 1, b = 2, and c = – 1 to solve for cos x. 87 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 4 Solving a Trigonometric Equation Using the Quadratic Formula (cont. ) Since there are two solutions, one in quadrant I and the other in quadrant IV. Since this value of cos x. , there are no solutions for To find all solutions, add integer multiples of the period of cosine, 2 88 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 5 Solving a Trigonometric Equation by Squaring (page 703) Square both sides. The possible solutions are 89 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 5 Solving a Trigonometric Equation by Squaring (cont. ) Since the solution was found by squaring both sides of an equation, we must check that each proposed solution is a solution of the original equation. Not a solution Solution 90 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

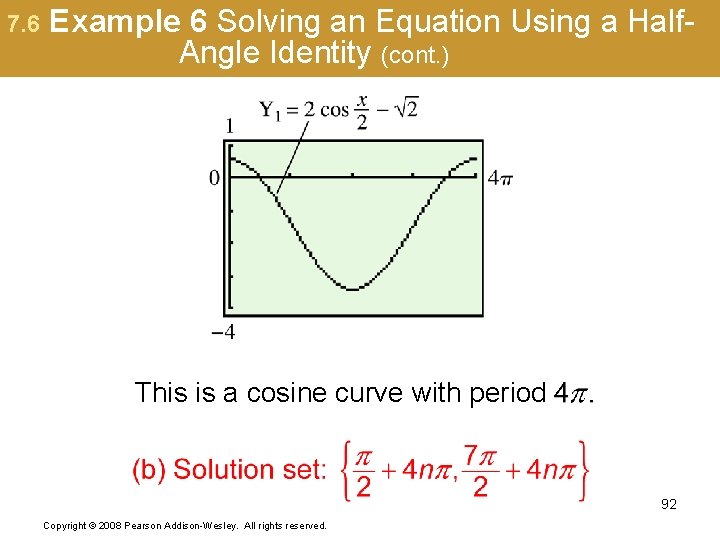
7. 6 Example 6 Solving an Equation Using a Half. Angle Identity (page 704) (a) over the interval and (b) give all solutions. is not in the requested domain. 91 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 6 Solving an Equation Using a Half. Angle Identity (cont. ) This is a cosine curve with period 92 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 7 Solving an Equation With a Double Angle (page 705) Factor. or 93 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 8 Solving an Equation Using a Multiple Angle Identity (page 705) From the given interval 0° ≤ θ < 360°, the interval for 2θ is 0° ≤ 2θ < 720°. 94 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 8 Solving an Equation Using a Multiple Angle Identity (cont. ) Since cosine is negative in quadrants II and III, solutions over this interval are 95 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

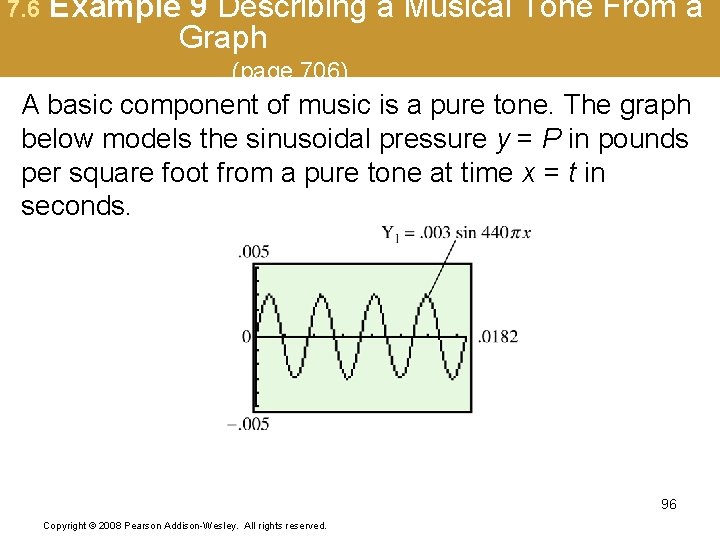
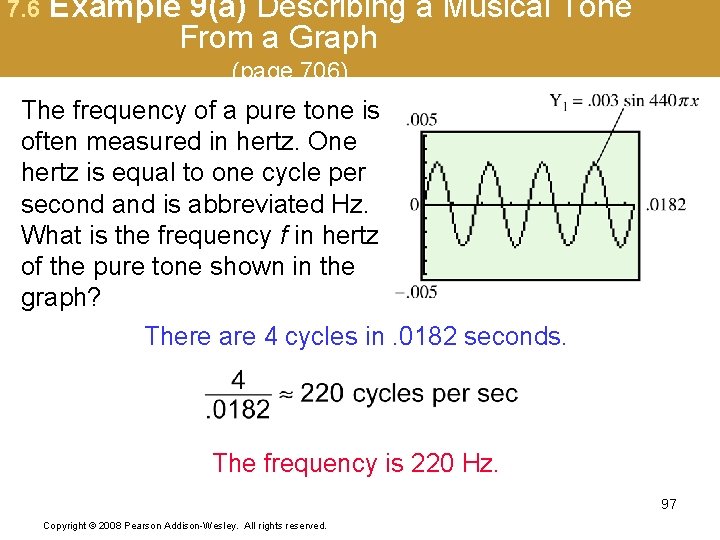
7. 6 Example 9 Describing a Musical Tone From a Graph (page 706) A basic component of music is a pure tone. The graph below models the sinusoidal pressure y = P in pounds per square foot from a pure tone at time x = t in seconds. 96 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 9(a) Describing a Musical Tone From a Graph (page 706) The frequency of a pure tone is often measured in hertz. One hertz is equal to one cycle per second and is abbreviated Hz. What is the frequency f in hertz of the pure tone shown in the graph? There are 4 cycles in. 0182 seconds. The frequency is 220 Hz. 97 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

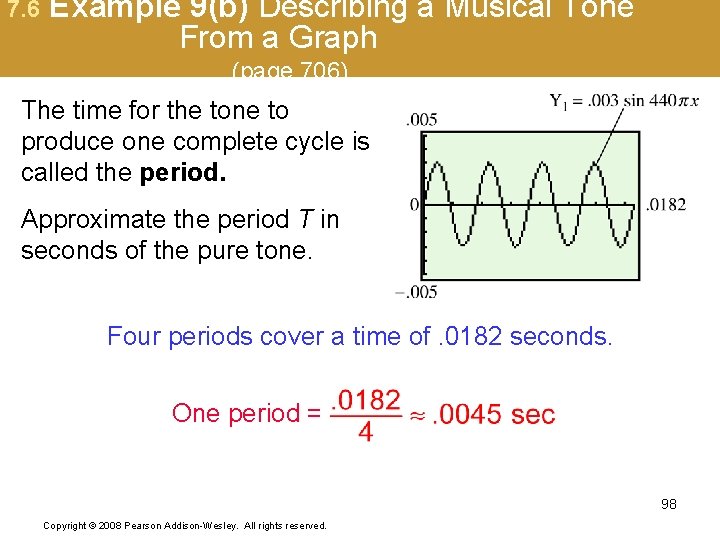
7. 6 Example 9(b) Describing a Musical Tone From a Graph (page 706) The time for the tone to produce one complete cycle is called the period. Approximate the period T in seconds of the pure tone. Four periods cover a time of. 0182 seconds. One period = 98 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

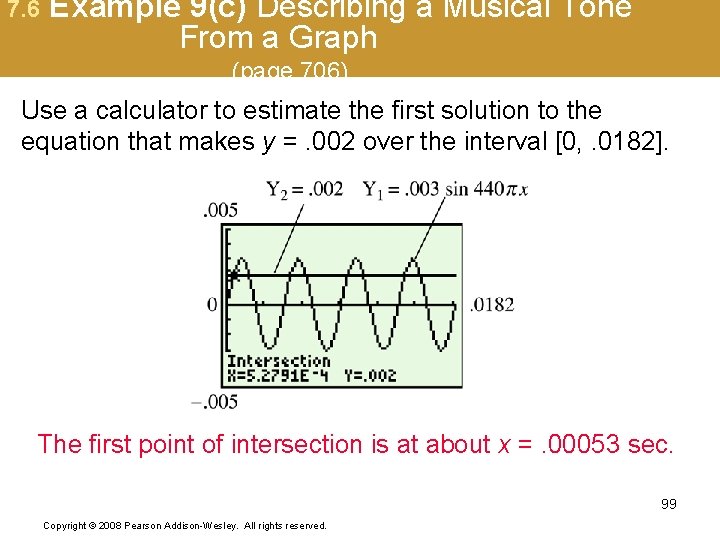
7. 6 Example 9(c) Describing a Musical Tone From a Graph (page 706) Use a calculator to estimate the first solution to the equation that makes y =. 002 over the interval [0, . 0182]. The first point of intersection is at about x =. 00053 sec. 99 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 10 Analyzing Pressures of Upper Harmonics (page 707) Suppose that the E key above middle C is played on a piano. Its fundamental frequency is and its associate pressure is expressed as (a) What are the next four frequencies at which the string will vibrate? 100 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 6 Example 10 Analyzing Pressures of Upper Harmonics (cont. ) (b) What are the pressures corresponding to these four upper harmonics? 101 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Equations Involving Inverse Trigonometric Functions Solving for x in Terms of y Using Inverse Functions ▪ Solving Inverse Trigonometric Equations 102 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 1 Solving an Equation for a Variable Using Inverse Notation (page 713) 103 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 2 Solving an Equation Involving an Inverse Trigonometric Function (page 713) 104 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

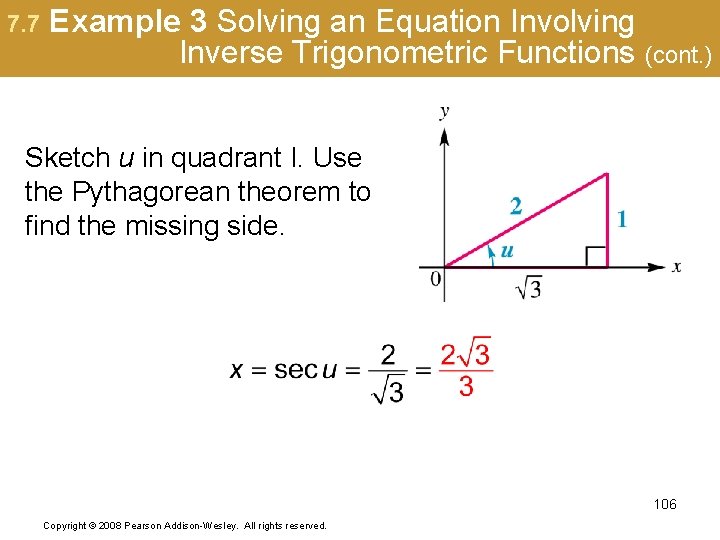
7. 7 Example 3 Solving an Equation Involving Inverse Trigonometric Functions (page 714) 105 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 3 Solving an Equation Involving Inverse Trigonometric Functions (cont. ) Sketch u in quadrant I. Use the Pythagorean theorem to find the missing side. 106 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (page 714) Isolate one inverse function on one side of the equation: Sine difference identity By definition, the arcsine function is defined in quadrants I and IV, so Copyright © 2008 Pearson Addison-Wesley. All rights reserved. 107

7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (cont. ) From equation (1), By definition, the range of arccos x is so the intersection of the two ranges is Sketch u in Quadrant III. Use the Pythagorean theorem to find the missing side. 108 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (cont. ) Substitute into equation (2): Square both sides. 109 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (cont. ) Check each potential solution. There is no value of x in the given domain such that 110 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

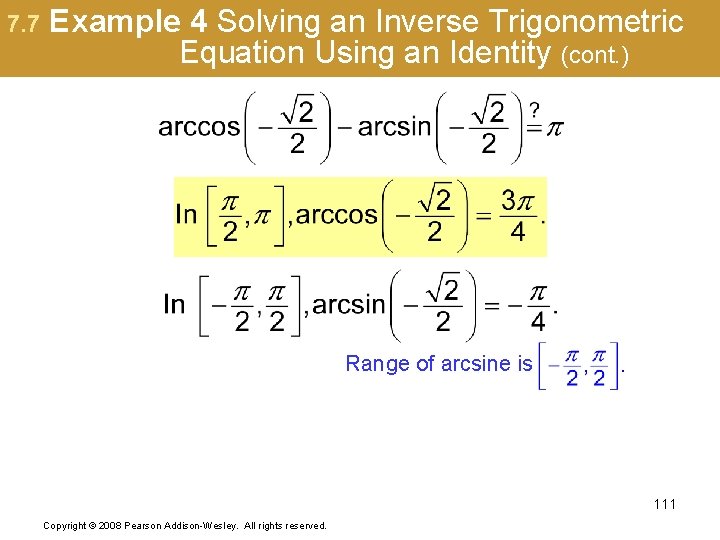
7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (cont. ) Range of arcsine is 111 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.

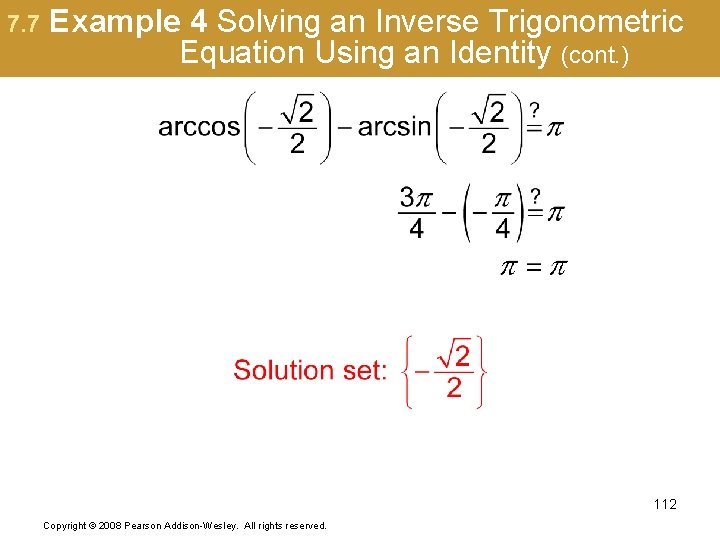
7. 7 Example 4 Solving an Inverse Trigonometric Equation Using an Identity (cont. ) 112 Copyright © 2008 Pearson Addison-Wesley. All rights reserved.