7 Transverse Shear CHAPTER OBJECTIVES Develop a method

7. Transverse Shear CHAPTER OBJECTIVES • Develop a method for finding the shear stress in a beam having a prismatic x-section and made from homogeneous material that behaves in a linear -elastic manner • This method of analysis is limited to special cases of xsectional geometry • Discuss the concept of shear flow, with shear stress for beams and thin-walled members • Discuss the shear center 2005 Pearson Education South Asia Pte Ltd 1

7. Transverse Shear CHAPTER OUTLINE 1. 2. 3. 4. 5. 6. Shear in Straight Members The Shear Formula Shear Stresses in Beams Shear Flow in Built-up Members Shear Flow in Thin-Walled Members *Shear Center 2005 Pearson Education South Asia Pte Ltd 2

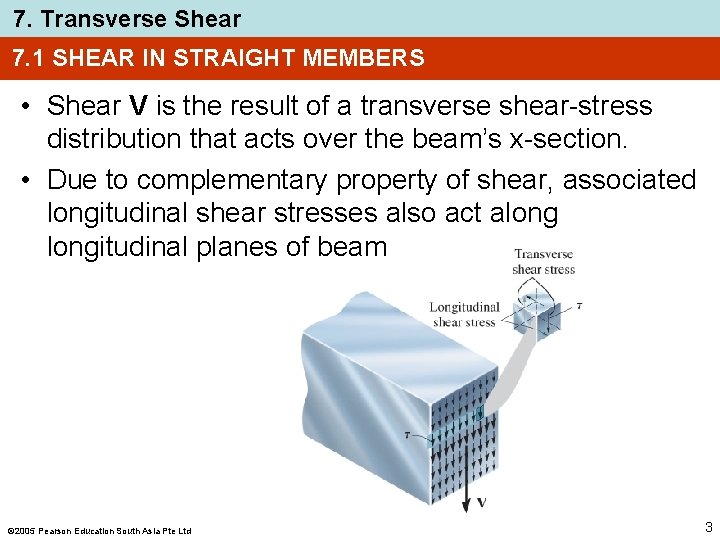
7. Transverse Shear 7. 1 SHEAR IN STRAIGHT MEMBERS • Shear V is the result of a transverse shear-stress distribution that acts over the beam’s x-section. • Due to complementary property of shear, associated longitudinal shear stresses also act alongitudinal planes of beam 2005 Pearson Education South Asia Pte Ltd 3

7. Transverse Shear 7. 1 SHEAR IN STRAIGHT MEMBERS • As shown below, if top and bottom surfaces of each board are smooth and not bonded together, then application of load P will cause the boards to slide relative to one another. • However, if boards are bonded together, longitudinal shear stresses will develop and distort x-section in a complex manner 2005 Pearson Education South Asia Pte Ltd 4

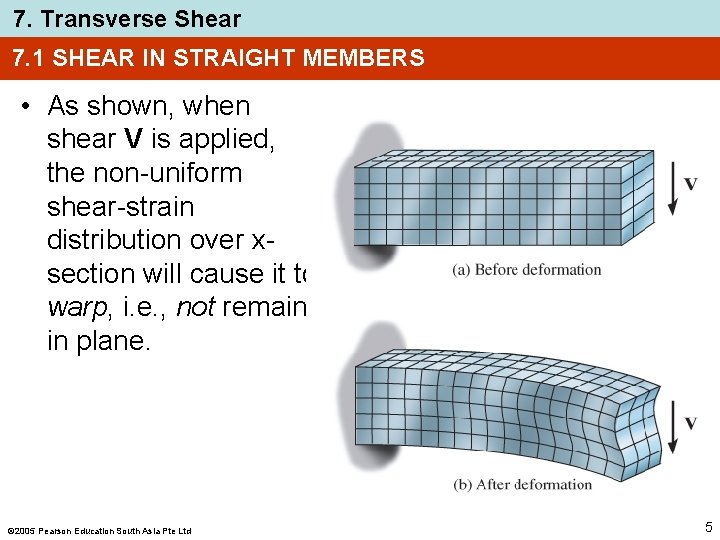
7. Transverse Shear 7. 1 SHEAR IN STRAIGHT MEMBERS • As shown, when shear V is applied, the non-uniform shear-strain distribution over xsection will cause it to warp, i. e. , not remain in plane. 2005 Pearson Education South Asia Pte Ltd 5

7. Transverse Shear 7. 1 SHEAR IN STRAIGHT MEMBERS • Recall that the flexure formula assumes that xsections must remain plane and perpendicular to longitudinal axis of beam after deformation • This is violated when beam is subjected to both bending and shear, we assume that the warping is so small it can be neglected. This is true for a slender beam (small depth compared with its length) • For transverse shear, shear-strain distribution throughout the depth of a beam cannot be easily expressed mathematically 2005 Pearson Education South Asia Pte Ltd 6

7. Transverse Shear 7. 1 SHEAR IN STRAIGHT MEMBERS • Thus, we need to develop the formula for shear stress is indirectly using the flexure formula and relationship between moment and shear (V = d. M/dx) 2005 Pearson Education South Asia Pte Ltd 7

7. Transverse Shear 7. 2 THE SHEAR FORMULA • By first principles, flexure formula and V = d. M/dx, we obtain VQ = It Equation 7 -3 = shear stress in member at the pt located a distance y’ from the neutral axis. Assumed to be constant and therefore averaged across the width t of member V = internal resultant shear force, determined from method of sections and equations of equilibrium 2005 Pearson Education South Asia Pte Ltd 8

7. Transverse Shear 7. 2 THE SHEAR FORMULA • By first principles, flexure formula and V = d. M/dx, we get: VQ = It Equation 7 -3 I = moment of inertia of entire x-sectional area computed about the neutral axis t = width of the member’s x-sectional area, measured at the pt where is to be determined Q = ∫A’ y d. A’ = y’A’, where A’ is the top (or bottom) portion of member’s x-sectional area, defined from section where t is measured, and y’ is distance of centroid of A’, measured from neutral axis 2005 Pearson Education South Asia Pte Ltd 9

7. Transverse Shear 7. 2 THE SHEAR FORMULA • The equation derived is called the shear formula • Since Eqn 7 -3 is derived indirectly from the flexure formula, the material must behave in a linearelastic manner and have a modulus of elasticity that is the same in tension and in compression • Shear stress in composite members can also be obtained using the shear formula • To do so, compute Q and I from the transformed section of the member as discussed in section 6. 6. Thickness t in formula remains the actual width t of x-section at the pt where is to be calculated 2005 Pearson Education South Asia Pte Ltd 10

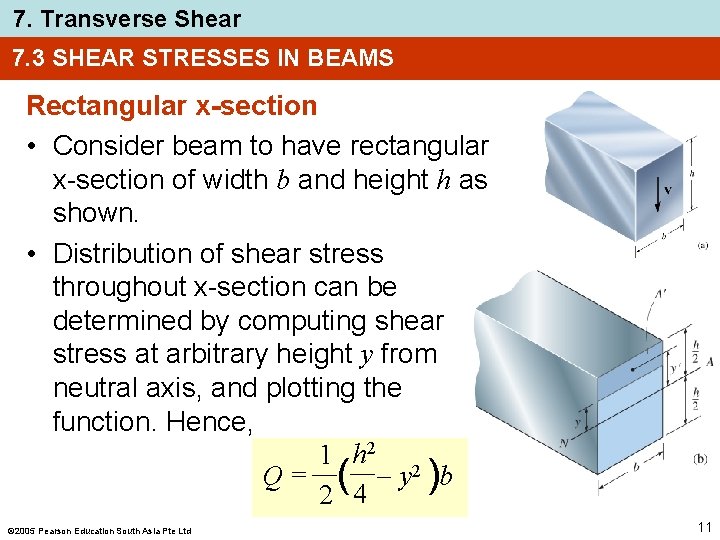
7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Rectangular x-section • Consider beam to have rectangular x-section of width b and height h as shown. • Distribution of shear stress throughout x-section can be determined by computing shear stress at arbitrary height y from neutral axis, and plotting the function. Hence, 1 h 2 2 Q = ( y )b 2 4 2005 Pearson Education South Asia Pte Ltd 11

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Rectangular x-section • After deriving Q and applying the shear formula, we have 6 V h 2 2 = y ) ( 3 bh 4 Equation 7 -4 • Eqn 7 -4 indicates that shear-stress distribution over x-section is parabolic. 2005 Pearson Education South Asia Pte Ltd 12

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Rectangular x-section • At y = 0, we have V max = 1. 5 A Equation 7 -5 • By comparison, max is 50% greater than the average shear stress determined from avg = V/A. 2005 Pearson Education South Asia Pte Ltd 13

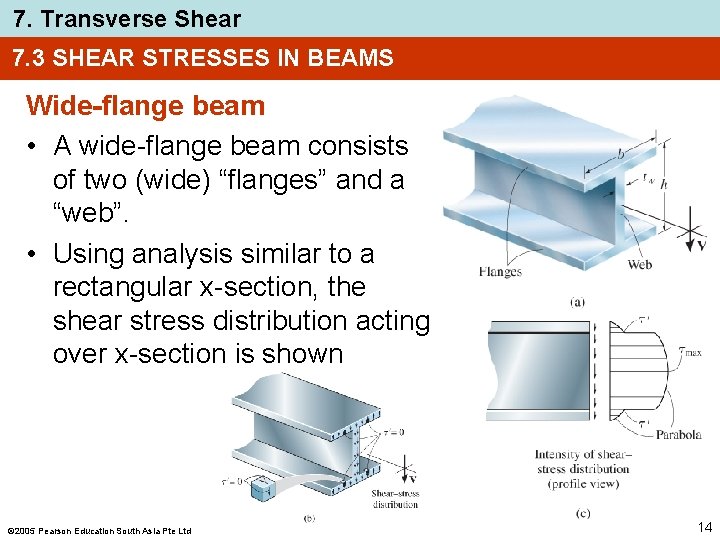
7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Wide-flange beam • A wide-flange beam consists of two (wide) “flanges” and a “web”. • Using analysis similar to a rectangular x-section, the shear stress distribution acting over x-section is shown 2005 Pearson Education South Asia Pte Ltd 14

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Wide-flange beam • The shear-stress distribution also varies parabolically over beam’s depth • Note there is a jump in shear stress at the flangeweb junction since x-sectional thickness changes at this pt • The web carries significantly more shear force than the flanges 2005 Pearson Education South Asia Pte Ltd 15

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Limitations on use of shear formula • One major assumption in the development of the shear formula is that shear stress is uniformly distributed over width t at section where shear stress is to be determined • By comparison with exact mathematical analysis based on theory of elasticity, the magnitude difference can reach 40% • This is especially so for the flange of a wide-flange beam 2005 Pearson Education South Asia Pte Ltd 16

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Limitations on use of shear formula • The shear formula will also give inaccurate results for the shear stress at the flange-web junction of a wide-flange beam, since this is a pt of sudden xsectional change (stress concentration occurs here) • Furthermore, inner regions of flanges are free boundaries, thus shear stress at these boundaries should be zero • However, shear formula calculated at these pts will not be zero 2005 Pearson Education South Asia Pte Ltd 17

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Limitations on use of shear formula • Fortunately, engineers are often interested in the average maximum shear stress, which occurs at the neutral axis, where b/h ratio is very small • Also, shear formula does not give accurate results when applied to members having x-sections that are short or flat, or at pts where the x-section suddenly changes • It should also not be applied across a section that intersects the boundary of a member at an angle other than 90 o 2005 Pearson Education South Asia Pte Ltd 18

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS IMPORTANT • Shear forces in beams cause non-linear shearstrain distributions over the x-section, causing it to warp • Due to complementary property of shear stress, the shear stress developed in a beam acts on both the x-section and on longitudinal planes • The shear formula was derived by considering horizontal force equilibrium of longitudinal shear stress and bending-stress distributions acting on a portion of a differential segment of the beam 2005 Pearson Education South Asia Pte Ltd 19

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS IMPORTANT • The shear formula is to be used on straight prismatic members made of homogeneous material that has linear-elastic behavior. Also, internal resultant shear force must be directed along an axis of symmetry for x-sectional area • For beam having rectangular x-section, shear stress varies parabolically with depth. • For beam having rectangular x-section, maximum shear stress is along neutral axis 2005 Pearson Education South Asia Pte Ltd 20

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS IMPORTANT • Shear formula should not be used to determine shear stress on x-sections that are short or flat, or at pts of sudden x-sectional changes, or at a pt on an inclined boundary 2005 Pearson Education South Asia Pte Ltd 21

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Procedure for analysis Internal shear • Section member perpendicular to its axis at the pt where shear stress is to be determined • Obtain internal shear V at the section Section properties • Determine location of neutral axis, and determine the moment of inertia I of entire x-sectional area about the neutral axis • Pass an imaginary horizontal section through the pt where the shear stress is to be determined 2005 Pearson Education South Asia Pte Ltd 22

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Procedure for analysis Section properties • Measure the width t of the area at this section • Portion of area lying either above or below this section is A’. • Determine Q either by integration, Q = ∫A’ y d. A’, or by using Q = y’A’. • Here, y’ is the distance of centroid of A’, measured from the neutral axis. (TIP: A’ is the portion of the member’s x-sectional area being “held onto the member” by the longitudinal shear stresses. ) 2005 Pearson Education South Asia Pte Ltd 23

7. Transverse Shear 7. 3 SHEAR STRESSES IN BEAMS Procedure for analysis Shear stress • Using consistent set of units, substitute data into the shear formula and compute shear stress • Suggest that proper direction of transverse shear stress be established on a volume element of material located at the pt where it is computed • acts on the x-section in the same direction as V. From this, corresponding shear stresses acting on the three other planes of element can be established 2005 Pearson Education South Asia Pte Ltd 24

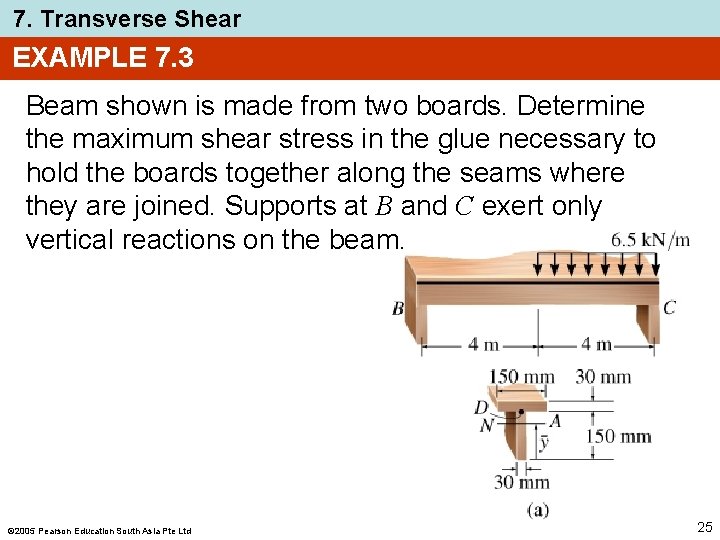
7. Transverse Shear EXAMPLE 7. 3 Beam shown is made from two boards. Determine the maximum shear stress in the glue necessary to hold the boards together along the seams where they are joined. Supports at B and C exert only vertical reactions on the beam. 2005 Pearson Education South Asia Pte Ltd 25

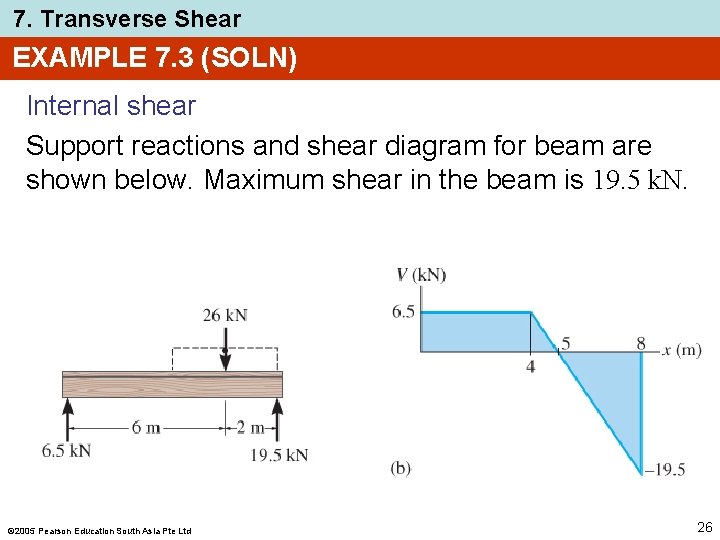
7. Transverse Shear EXAMPLE 7. 3 (SOLN) Internal shear Support reactions and shear diagram for beam are shown below. Maximum shear in the beam is 19. 5 k. N. 2005 Pearson Education South Asia Pte Ltd 26

7. Transverse Shear EXAMPLE 7. 3 (SOLN) Section properties The centroid and therefore the neutral axis will be determined from the reference axis placed at bottom of the x-sectional area. Working in units of meters, we have y. A y= =. . . = 0. 120 m A Thus, the moment of inertia, computed about the neutral axis is, I =. . . = 27. 0(10 -6) m 4 2005 Pearson Education South Asia Pte Ltd 27

7. Transverse Shear EXAMPLE 7. 3 (SOLN) Section properties The top board (flange) is being held onto the bottom board (web) by the glue, which is applied over the thickness t = 0. 03 m. Consequently A’ is defined as the area of the top board, we have Q = y’A’ = [(0. 180 m 0. 015 m 0. 120 m] (0. 03 m)(0. 150 m) Q = 0. 2025(10 -3) m 3 2005 Pearson Education South Asia Pte Ltd 28

7. Transverse Shear EXAMPLE 7. 3 (SOLN) Shear stress Using above data, and applying shear formula yields VQ max = =. . . = 4. 88 MPa It Shear stress acting at top of bottom board is shown here. It is the glue’s resistance to this lateral or horizontal shear stress that is necessary to hold the boards from slipping at support C. 2005 Pearson Education South Asia Pte Ltd 29

7. Transverse Shear 7. 4 SHEAR FLOW IN BUILT-UP MEMBERS • Occasionally, in engineering practice, members are “built-up” from several composite parts in order to achieve a greater resistance to loads, some examples are shown. • If loads cause members to bend, fasteners may be needed to keep component parts from sliding relative to one another. • To design the fasteners, we need to know the shear force resisted by fastener along member’s length 2005 Pearson Education South Asia Pte Ltd 30

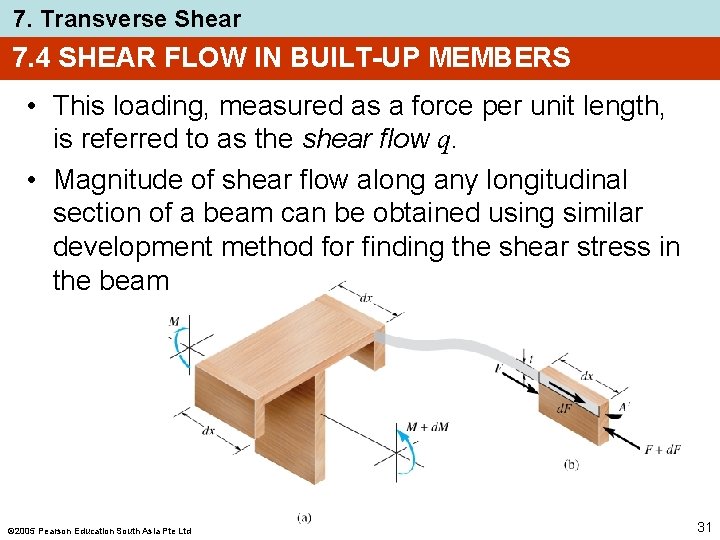
7. Transverse Shear 7. 4 SHEAR FLOW IN BUILT-UP MEMBERS • This loading, measured as a force per unit length, is referred to as the shear flow q. • Magnitude of shear flow along any longitudinal section of a beam can be obtained using similar development method for finding the shear stress in the beam 2005 Pearson Education South Asia Pte Ltd 31

7. Transverse Shear 7. 4 SHEAR FLOW IN BUILT-UP MEMBERS • Thus shear flow is q = VQ/I Equation 7 -6 q = shear flow, measured as a force per unit length along the beam V = internal resultant shear force, determined from method of sections and equations of equilibrium I = moment of inertia of entire x-sectional area computed about the neutral axis Q = ∫A’ y d. A’ = y’A’, where A’ is the x-sectional area of segment connected to beam at juncture where shear flow is to be calculated, and y’ is distance from neutral axis to centroid of A’ 2005 Pearson Education South Asia Pte Ltd 32

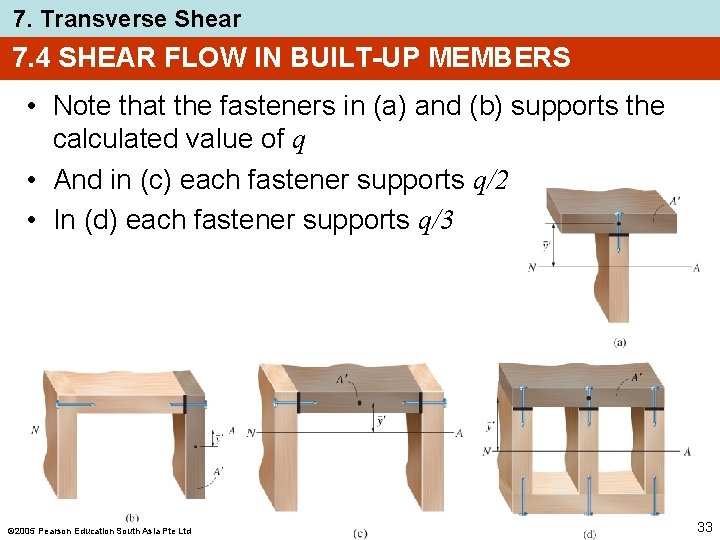
7. Transverse Shear 7. 4 SHEAR FLOW IN BUILT-UP MEMBERS • Note that the fasteners in (a) and (b) supports the calculated value of q • And in (c) each fastener supports q/2 • In (d) each fastener supports q/3 2005 Pearson Education South Asia Pte Ltd 33

7. Transverse Shear 7. 4 SHEAR FLOW IN BUILT-UP MEMBERS IMPORTANT • Shear flow is a measure of force per unit length along a longitudinal axis of a beam. • This value is found from the shear formula and is used to determine the shear force developed in fasteners and glue that holds the various segments of a beam together 2005 Pearson Education South Asia Pte Ltd 34

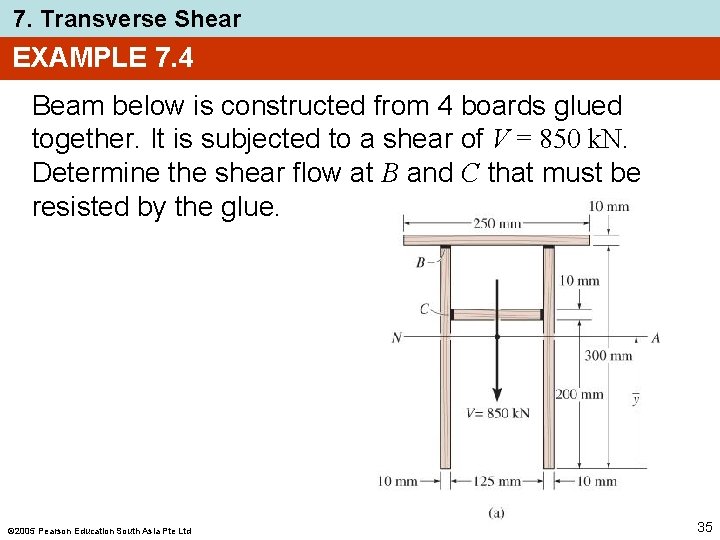
7. Transverse Shear EXAMPLE 7. 4 Beam below is constructed from 4 boards glued together. It is subjected to a shear of V = 850 k. N. Determine the shear flow at B and C that must be resisted by the glue. 2005 Pearson Education South Asia Pte Ltd 35

7. Transverse Shear EXAMPLE 7. 4 (SOLN) Section properties Neutral axis (centroid) is located from bottom of the beam. Working in units of meters, we have y. A y= =. . . = 0. 1968 m y Moment of inertia about neutral axis is I =. . . = 87. 52(10 -6) m 4 2005 Pearson Education South Asia Pte Ltd 36

7. Transverse Shear EXAMPLE 7. 4 (SOLN) Section properties Since the glue at B and B’ holds the top board to the beam, we have QB = y’B A’B = [0. 305 m 0. 1968 m](0. 250 m)(0. 01 m) QB = 0. 270(10 -3) m 3 Likewise, glue at C and C’ holds inner board to beam, so QC = y’C A’C =. . . = 0. 01025(10 -3) m 3 2005 Pearson Education South Asia Pte Ltd 37

7. Transverse Shear EXAMPLE 7. 4 (SOLN) Shear flow For B and B’, we have q’B = VQB /I = [850 k. N(0. 270(10 -3) m 3]/87. 52(10 -6) m 4 q’B = 2. 62 MN/m Similarly, for C and C’, q’C = VQC /I = [850 k. N(0. 0125(10 -3) m 3]/87. 52(10 -6) m 4 q’C = 0. 0995 MN/m 2005 Pearson Education South Asia Pte Ltd 38

7. Transverse Shear EXAMPLE 7. 4 (SOLN) Shear flow Since two seams are used to secure each board, the glue per meter length of beam at each seam must be strong enough to resist one-half of each calculated value of q’. Thus q. B = 1. 31 MN/m q. C = 0. 0498 MN/m 2005 Pearson Education South Asia Pte Ltd 39

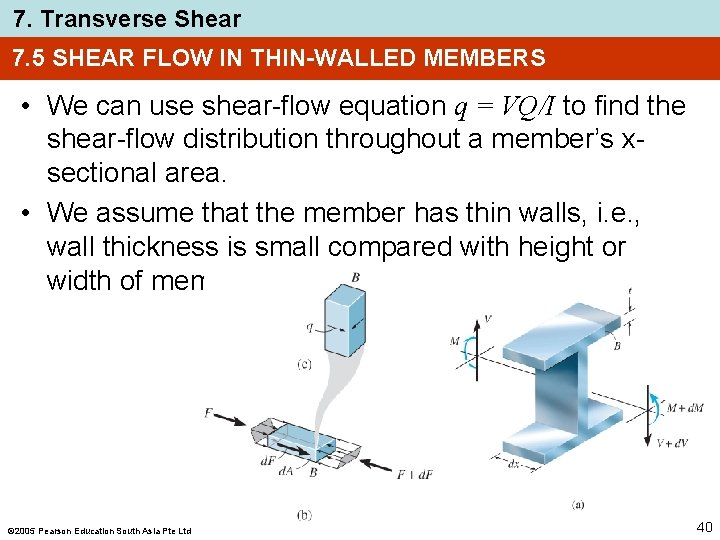
7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • We can use shear-flow equation q = VQ/I to find the shear-flow distribution throughout a member’s xsectional area. • We assume that the member has thin walls, i. e. , wall thickness is small compared with height or width of member 2005 Pearson Education South Asia Pte Ltd 40

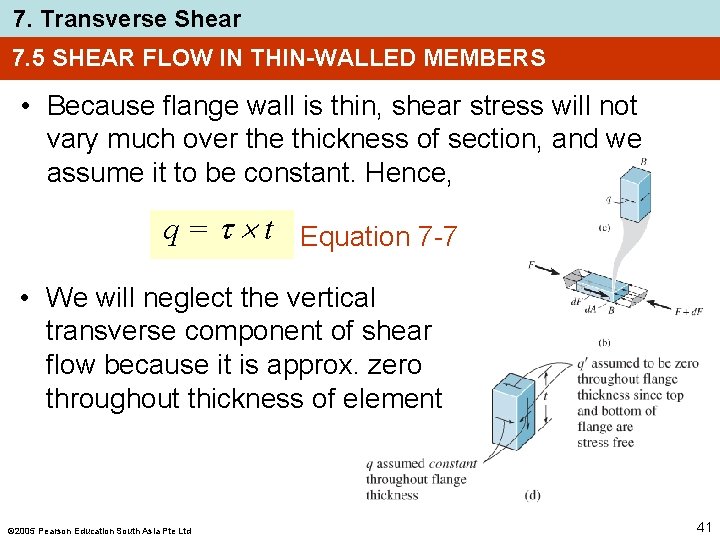
7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • Because flange wall is thin, shear stress will not vary much over the thickness of section, and we assume it to be constant. Hence, q = t Equation 7 -7 • We will neglect the vertical transverse component of shear flow because it is approx. zero throughout thickness of element 2005 Pearson Education South Asia Pte Ltd 41

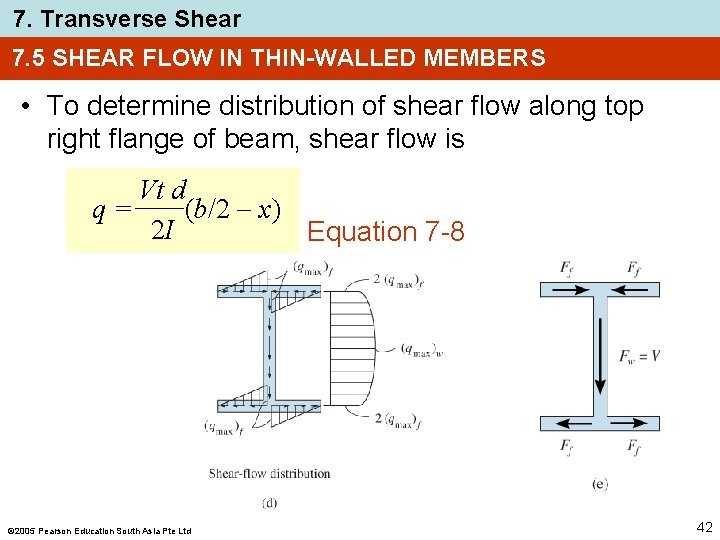
7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • To determine distribution of shear flow along top right flange of beam, shear flow is Vt d q= (b/2 x) 2 I Equation 7 -8 2005 Pearson Education South Asia Pte Ltd 42

7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • Similarly, for the web of the beam, shear flow is Vt db q = [ +0. 5(d 2/4 y 2)] I 2 Equation 7 -9 2005 Pearson Education South Asia Pte Ltd 43

7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • Value of q changes over the x-section, since Q will be different for each area segment A’ • q will vary linearly along segments (flanges) that are perpendicular to direction of V, and parabolically along segments (web) that are inclined or parallel to V • q will always act parallel to the walls of the member, since section on which q is calculated is taken perpendicular to the walls 2005 Pearson Education South Asia Pte Ltd 44

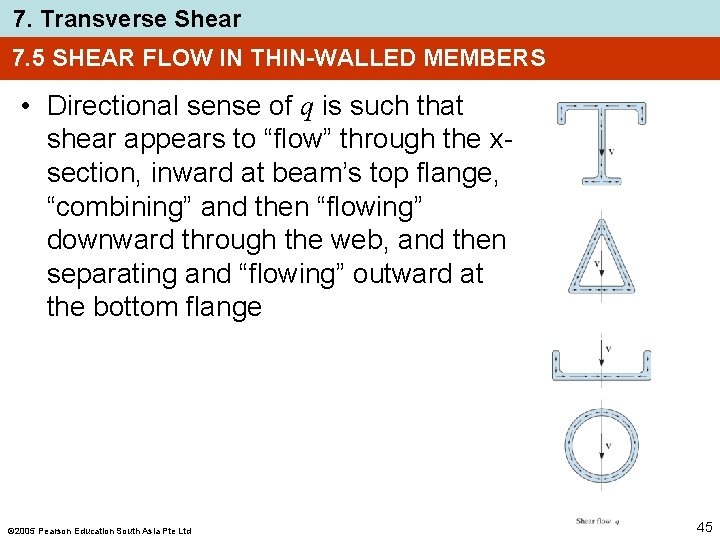
7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS • Directional sense of q is such that shear appears to “flow” through the xsection, inward at beam’s top flange, “combining” and then “flowing” downward through the web, and then separating and “flowing” outward at the bottom flange 2005 Pearson Education South Asia Pte Ltd 45

7. Transverse Shear 7. 5 SHEAR FLOW IN THIN-WALLED MEMBERS IMPORTANT • If a member is made from segments having thin walls, only the shear flow parallel to the walls of member is important • Shear flow varies linearly along segments that are perpendicular to direction of shear V • Shear flow varies parabolically along segments that are inclined or parallel to direction of shear V • On x-section, shear “flows” along segments so that it contributes to shear V yet satisfies horizontal and vertical force equilibrium 2005 Pearson Education South Asia Pte Ltd 46

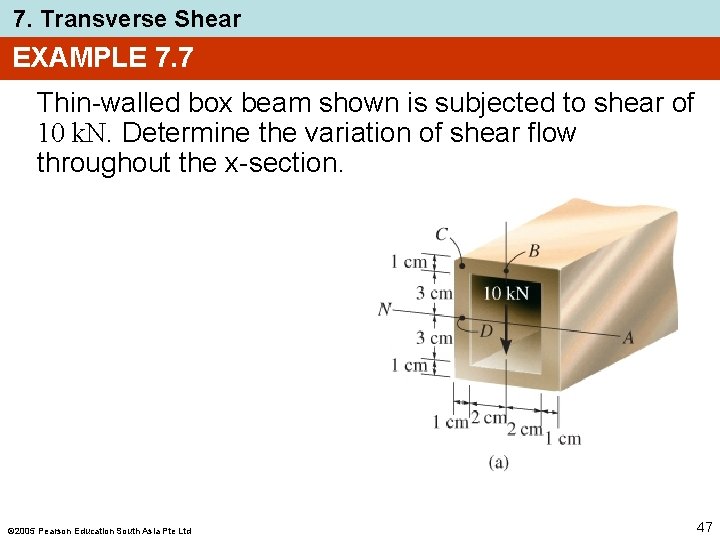
7. Transverse Shear EXAMPLE 7. 7 Thin-walled box beam shown is subjected to shear of 10 k. N. Determine the variation of shear flow throughout the x-section. 2005 Pearson Education South Asia Pte Ltd 47

7. Transverse Shear EXAMPLE 7. 7 (SOLN) By symmetry, neutral axis passes through center of x -section. Thus moment of inertia is I = 1/12(6 cm)(8 cm)3 1/12(4 cm)(6 cm)3 = 184 cm 4 Only shear flows at pts B, C and D needs to be determined. For pt B, area A’ ≈ 0 since it can be thought of located entirely at pt B. Alternatively, A’ can also represent the entire xsectional area, in which case QB = y’A’ = 0 since y’ = 0. 2005 Pearson Education South Asia Pte Ltd 48

7. Transverse Shear EXAMPLE 7. 7 (SOLN) Because QB = 0, then q. B = 0 For pt C, area A’ is shown dark-shaded. Here mean dimensions are used since pt C is on centerline of each segment. We have QC = y’A’ = (3. 5 cm)(1 cm) = 17. 5 cm 3 q. C = VQC/I =. . . = 95. 1 N/mm 2005 Pearson Education South Asia Pte Ltd 49

7. Transverse Shear EXAMPLE 7. 7 (SOLN) Shear flow at D is computed using the three dark-shaded rectangles shown. We have QD = y’A’ =. . . = 30 cm 3 q. C = VQD/I =. . . = 163 N/mm 2005 Pearson Education South Asia Pte Ltd 50

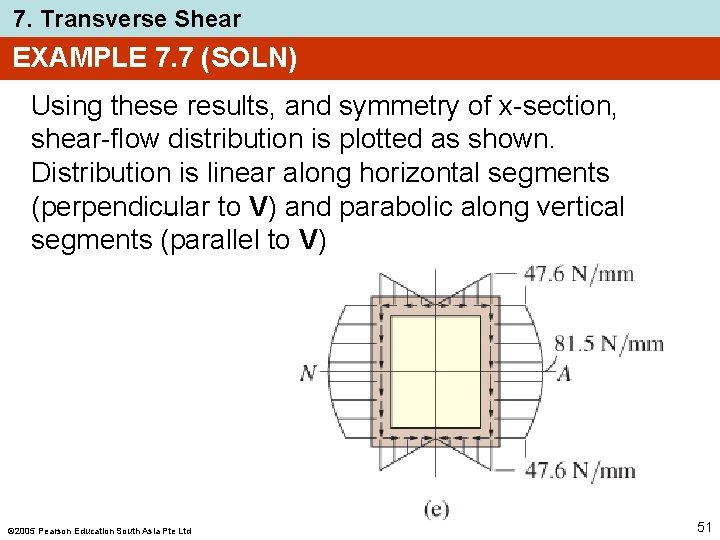
7. Transverse Shear EXAMPLE 7. 7 (SOLN) Using these results, and symmetry of x-section, shear-flow distribution is plotted as shown. Distribution is linear along horizontal segments (perpendicular to V) and parabolic along vertical segments (parallel to V) 2005 Pearson Education South Asia Pte Ltd 51

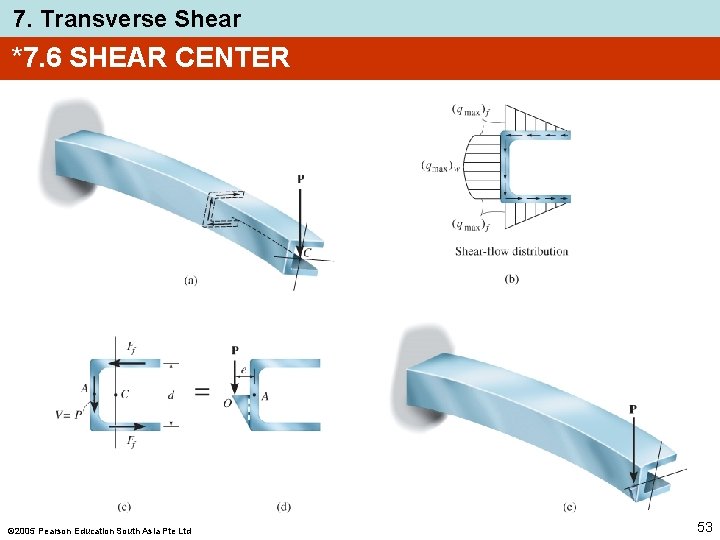
7. Transverse Shear *7. 6 SHEAR CENTER • Previously, we assumed that internal shear V was applied along a principal centroidal axis of inertia that also represents the axis of symmetry for the x -section • Here, we investigate the effect of applying the shear along a principal centroidal axis that is not an axis of symmetry • When a force P is applied to a channel section along the once vertical unsymmetrical axis that passes through the centroid C of the x-sectional area, the channel bends downwards and also twist clockwise 2005 Pearson Education South Asia Pte Ltd 52

7. Transverse Shear *7. 6 SHEAR CENTER 2005 Pearson Education South Asia Pte Ltd 53

7. Transverse Shear *7. 6 SHEAR CENTER • When the shear-flow distribution is integrated over the flange and web areas, a resultant force of Ff in each flange and a force of V=P in the web is created • If we sum the moments of these forces about pt A, the couple (or torque) created by the flange forces causes the member to twist • To prevent the twisting, we need to apply P at a pt O located a distance e from the web of the channel, thus MA = Ff d = Pe e = (Ff d)/P 2005 Pearson Education South Asia Pte Ltd 54

7. Transverse Shear *7. 6 SHEAR CENTER • Express Ff is expressed in terms of P (= V) and dimensions of flanges and web to reduce e as a function of its x-sectional geometry • We name the pt O as the shear center or flexural center • When P is applied at the shear center, beam will bend without twisting • Note that shear center will always lie on an axis of symmetry of a member’s x-sectional area 2005 Pearson Education South Asia Pte Ltd 55

7. Transverse Shear *7. 6 SHEAR CENTER IMPORTANT • Shear center is the pt through which a force can be applied which will cause a beam to bend and yet not twist • Shear center will always lie on an axis of symmetry of the x-section • Location of the shear center is only a function of the geometry of the x-section and does not depend upon the applied loading 2005 Pearson Education South Asia Pte Ltd 56

7. Transverse Shear *7. 6 SHEAR CENTER Procedure for analysis Shear-flow resultants • Magnitudes of force resultants that create a moment about pt A must be calculated • For each segment, determine the shear flow q at an arbitrary pt on segment and then integrate q along the segment’s length • Note that V will create a linear variation of shear flow in segments that are perpendicular to V and a parabolic variation of shear flow in segments that are parallel or inclined to V 2005 Pearson Education South Asia Pte Ltd 57

7. Transverse Shear *7. 6 SHEAR CENTER Procedure for analysis Shear-flow resultants • Determine the direction of shear flow through the various segments of the x-section • Sketch the force resultants on each segment of the x-section • Since shear center determined by taking the moments of these force resultants about a pt (A), choose this pt at a location that eliminates the moments of as many as force resultants as possible 2005 Pearson Education South Asia Pte Ltd 58

7. Transverse Shear *7. 6 SHEAR CENTER Procedure for analysis Shear center • Sum the moments of the shear-flow resultants about pt A and set this moment equal to moment of V about pt A • Solve this equation and determine the momentarm distance e, which locates the line of action of V from pt A • If axis of symmetry for x-section exists, shear center lies at the pt where this axis intersects line of action of V 2005 Pearson Education South Asia Pte Ltd 59

7. Transverse Shear *7. 6 SHEAR CENTER Procedure for analysis Shear center • If no axes of symmetry exists, rotate the x-section o by 90 and repeat the process to obtain another line of action for V • Shear center then lies at the pt of intersection of the o two 90 lines 2005 Pearson Education South Asia Pte Ltd 60

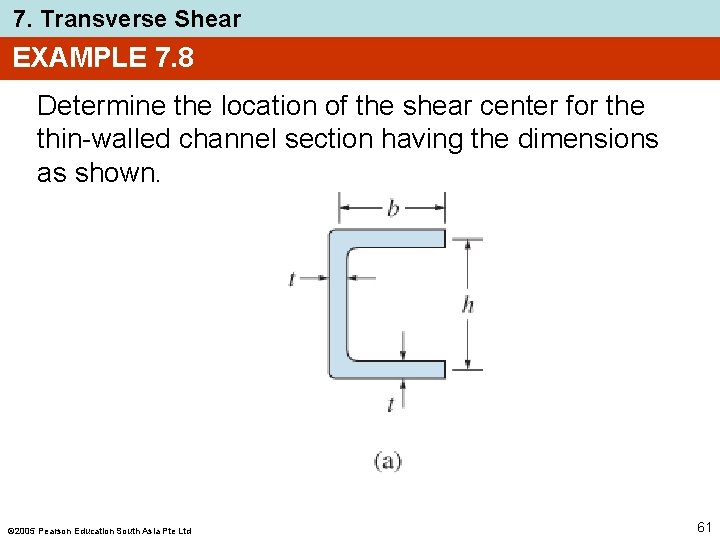
7. Transverse Shear EXAMPLE 7. 8 Determine the location of the shear center for the thin-walled channel section having the dimensions as shown. 2005 Pearson Education South Asia Pte Ltd 61

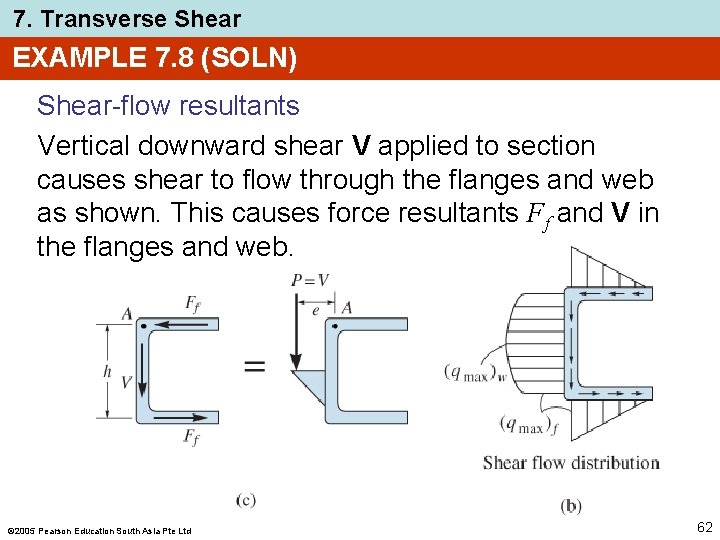
7. Transverse Shear EXAMPLE 7. 8 (SOLN) Shear-flow resultants Vertical downward shear V applied to section causes shear to flow through the flanges and web as shown. This causes force resultants Ff and V in the flanges and web. 2005 Pearson Education South Asia Pte Ltd 62

7. Transverse Shear EXAMPLE 7. 8 (SOLN) Shear-flow resultants X-sectional area than divided into 3 component rectangles: a web and 2 flanges. Assume each component to be thin, then moment of inertia about the neutral axis is I = (1/12)th 3 + 2[bt(0. 5 h)2] = (0. 5 th 2)[(h/6) + b] Thus, q at the arbitrary position x is VQ V(b – x) q= = I h[(h/6) + b] 2005 Pearson Education South Asia Pte Ltd 63

7. Transverse Shear EXAMPLE 7. 8 (SOLN) Shear-flow resultants Hence, b Ff = ∫ 0 q dx = … = Vb 2 2 h[(h/6) + b] The same result can be determined by first finding (qmax)f, then determining triangular area 0. 5 b(qmax)f = Ff 2005 Pearson Education South Asia Pte Ltd 64

7. Transverse Shear EXAMPLE 7. 8 (SOLN) Shear center Summing moments about pt A, we require Ve = Ff h … b 2 e= [(h/3) + 2 b] As stated previously, e depends only on the geometry of the xsection. 2005 Pearson Education South Asia Pte Ltd 65

7. Transverse Shear CHAPTER REVIEW • Transverse shear stress in beams is determined indirectly by using the flexure formula and the relationship between moment and shear (V = d. M/dx). This result in the shear formula = VQ/It. • In particular, the value for Q is the moment of the area A’ about the neutral axis. This area is the portion of the x-sectional area that is “held on” to the beam above thickness t where is to be determined 2005 Pearson Education South Asia Pte Ltd 66

7. Transverse Shear CHAPTER REVIEW • If the beam has a rectangular x-section, then the shear-stress distribution will be parabolic, obtaining a maximum value at the neutral axis • Fasteners, glues, or welds are used to connect the composite parts of a “built-up” section. The strength of these fasteners is determined from the shear flow, or force per unit length, that must be carried by the beam; q = VQ/I • If the beam has a thin-walled x-section the shear flow throughout the x-section can be determined by using q = VQ/I 2005 Pearson Education South Asia Pte Ltd 67

7. Transverse Shear CHAPTER REVIEW • The shear flow varies linearly along horizontal segments and parabolically along inclined or vertical segments • Provided the shear stress distribution in each element of a thin-walled section is known, then, using a balance of moments, the location of the shear center for the x-section can be determined. • When a load is applied to the member through this pt, the member will bend, and not twist 2005 Pearson Education South Asia Pte Ltd 68