7 th lecture Normal Shock Waves A pressure

7 th lecture Normal Shock Waves A pressure difference exists across a compression pulse. When this difference is sufficiently large, there is also an increase in entropy across the pulse. The flow is no longer isentropic and the wave is called a compression shock wave.

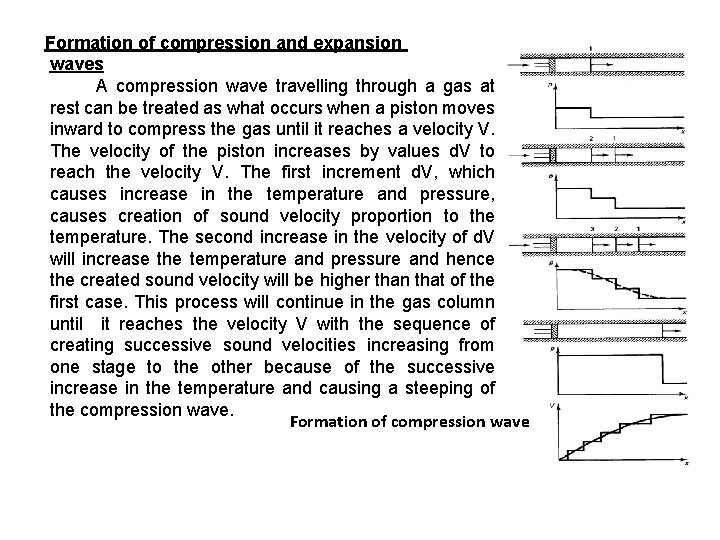
Formation of compression and expansion waves A compression wave travelling through a gas at rest can be treated as what occurs when a piston moves inward to compress the gas until it reaches a velocity V. The velocity of the piston increases by values d. V to reach the velocity V. The first increment d. V, which causes increase in the temperature and pressure, causes creation of sound velocity proportion to the temperature. The second increase in the velocity of d. V will increase the temperature and pressure and hence the created sound velocity will be higher than that of the first case. This process will continue in the gas column until it reaches the velocity V with the sequence of creating successive sound velocities increasing from one stage to the other because of the successive increase in the temperature and causing a steeping of the compression wave. Formation of compression wave

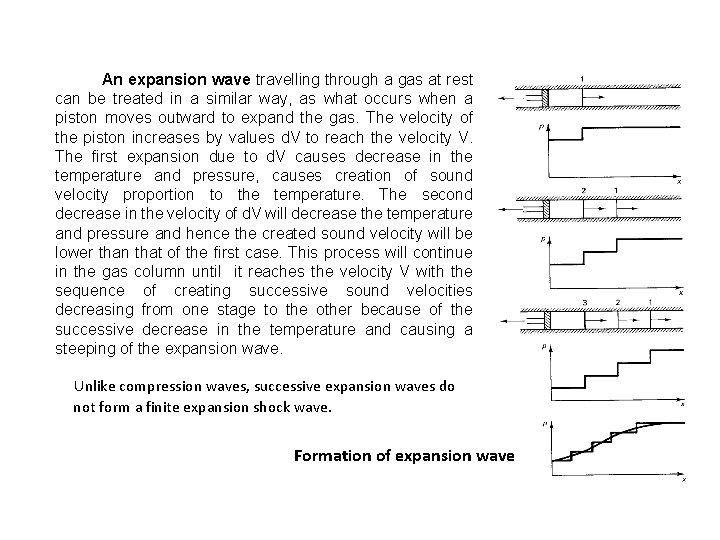
An expansion wave travelling through a gas at rest can be treated in a similar way, as what occurs when a piston moves outward to expand the gas. The velocity of the piston increases by values d. V to reach the velocity V. The first expansion due to d. V causes decrease in the temperature and pressure, causes creation of sound velocity proportion to the temperature. The second decrease in the velocity of d. V will decrease the temperature and pressure and hence the created sound velocity will be lower than that of the first case. This process will continue in the gas column until it reaches the velocity V with the sequence of creating successive sound velocities decreasing from one stage to the other because of the successive decrease in the temperature and causing a steeping of the expansion wave. Unlike compression waves, successive expansion waves do not form a finite expansion shock wave. Formation of expansion wave

Consider a normal shock wave propagating adiabatically through a gas in a duct of constant cross-sectional area A, as shown in the figure. Let subscripts x and y refer to the conditions just before and just after the shock. The continuity equation applied to a control surface surrounding the shock is: Applying the momentum equation and neglecting the friction forces because thickness of the shock is small: The energy equation is applied for adiabatic steady flow: The entropy will increase across the shock , as it is irreversible adiabatic:

Properties of gas after the shock will be derived: The stagnation temperature remains before and after the shock constant: And hence then From the continuity equation

Combining the last equations

Since a shock does not change the mass flow rate or stagnation temperature, the stagnation pressures across the shock are related to the critical areas as:

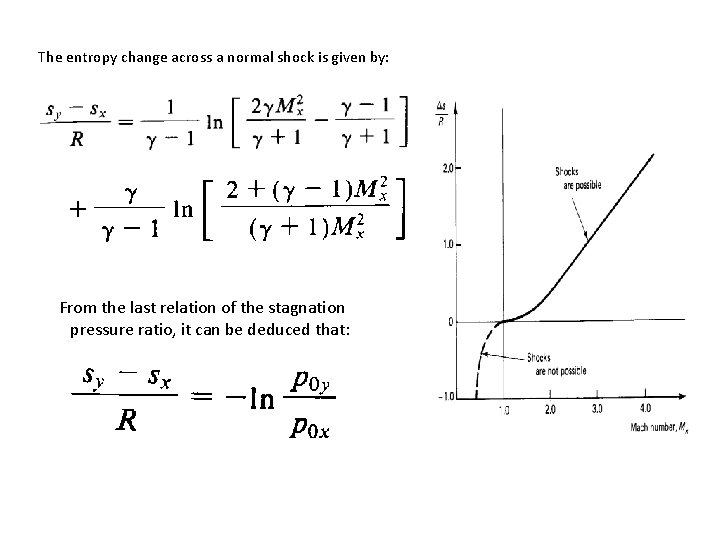
The entropy change across a normal shock is given by: From the last relation of the stagnation pressure ratio, it can be deduced that:

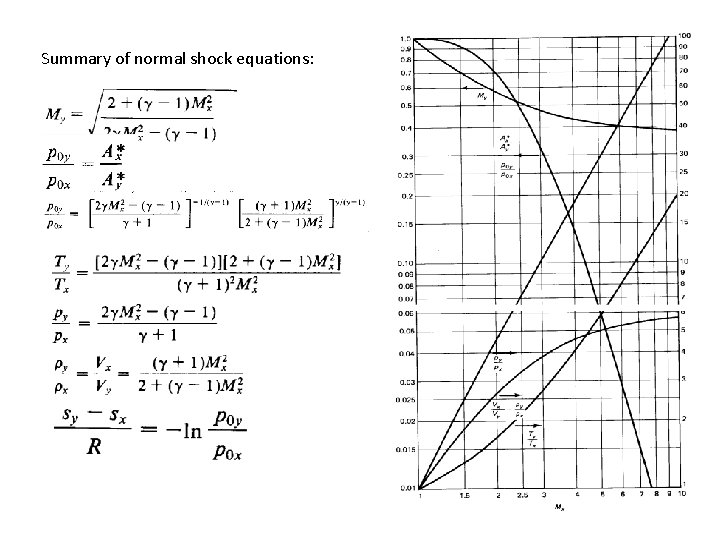
Summary of normal shock equations:

Prandtl relations

If the momentum equation is divided by the continuity equation we get: Substituting the last two equations:

This equation is called Prandtl relation

These two equations are called Rankine-Hugoniot relations.

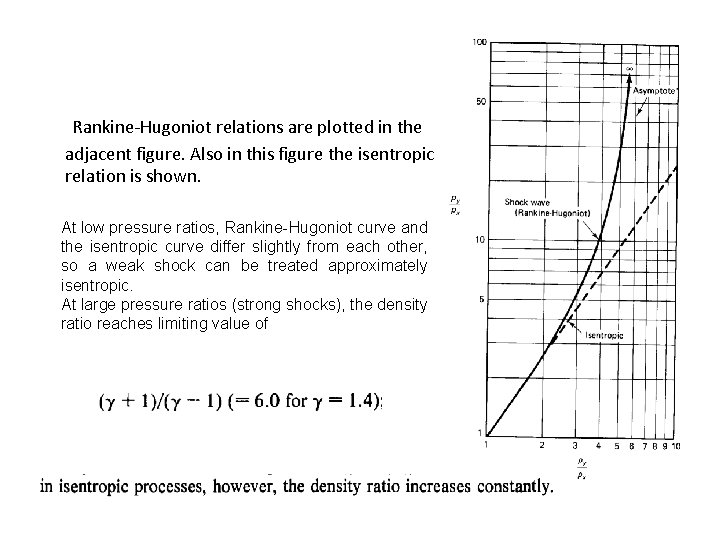
Rankine-Hugoniot relations are plotted in the adjacent figure. Also in this figure the isentropic relation is shown. At low pressure ratios, Rankine-Hugoniot curve and the isentropic curve differ slightly from each other, so a weak shock can be treated approximately isentropic. At large pressure ratios (strong shocks), the density ratio reaches limiting value of