7 TESTING OF HYPOTHESIS 7 TYPES OF STATISTICS

7 TESTING OF HYPOTHESIS

7

TYPES OF STATISTICS 1) Descriptive statistics 2) Inferential statistics

1) Descriptive Statistics Describe the characteristics of a body of data Example: Average of the student is 19 years.

2) Inferential Statistics It deals with those methods where conclusions about a large group are drawn by studying a part of it. Example Checking a few grains of rice a housewife makes an estimate whether the whole lot has been cooked.

POPULATION A population is any entire collection of people, animals, plants or things from which we may collect data. It is the entire group we are interested in, which we wish to describe or draw conclusions about.

SAMPLE A sample is a group of units selected from a larger group (the population). By studying the sample it is hoped to draw valid conclusions about the larger group.

PARAMETER Parameter is a numerical measurement that describes a characteristic of a population.

STATISTIC A statistic is a quantity that is calculated from a sample of data. It is used to give information about unknown values in the corresponding population.

HYPOTHESIS Assumption/Assertion/ guess/ statement about the parameter or random variables involved in the problem.

Testing of Hypothesis To verify our assumption is correct or not.

Testing of Hypothesis Procedure Null Hypothesis Alternative Hypothesis Level of Significance Test Statistic Critical Region/Table Value Inference

1) Null Hypothesis The sample have been drawn from the same population. Example: Ho : = 22000 km The average lifetime of a certain kind of tyre is 22000 km.

2) Alternative Hypothesis The sample have been drawn from the different population. Example: H 1 0 r H A : ≠ 22000 km The average lifetime of a certain kind of tyre is not 22000 km.

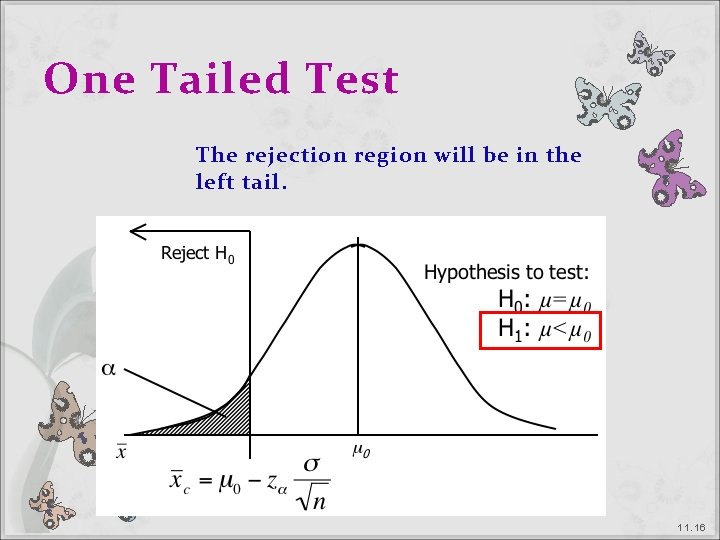
One Tailed Test The rejection region will be in the left tail. 1 1. 1 6

One Tailed Test The Rejection Region will be the right tail. Hypothesis to test H 0 : μ = 170 H 1 : μ > 170 1 1. 1 7

Two Tailed Test The rejection region is split equally between the two tails. 1 1. 1 8

3) Level of Significance The Maximum probability of committing Type I Error, which is specified in a test, is known as the level of significance.

Types of Error 1) Type I Error: When the NH is true, wrongly reject the NH. 2) Type II Error: When the NH is wrong, wrongly accept the NH.

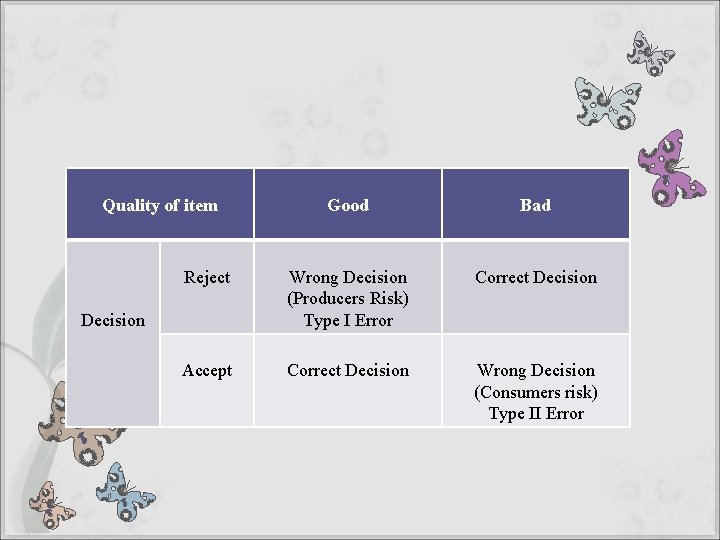
Quality of item Good Bad Reject Wrong Decision (Producers Risk) Type I Error Correct Decision Accept Correct Decision Wrong Decision (Consumers risk) Type II Error Decision

Type I and Type II Error Statistical Decision Reject H 0 Do not reject H 0 True state of null hypothesis H 0 True H 0 False Type I error (α) Correct Type II Error (β)

4) Test Statistic Choose the appropriate test based on the distribution Test statistic = sample value – population value/ standard Error

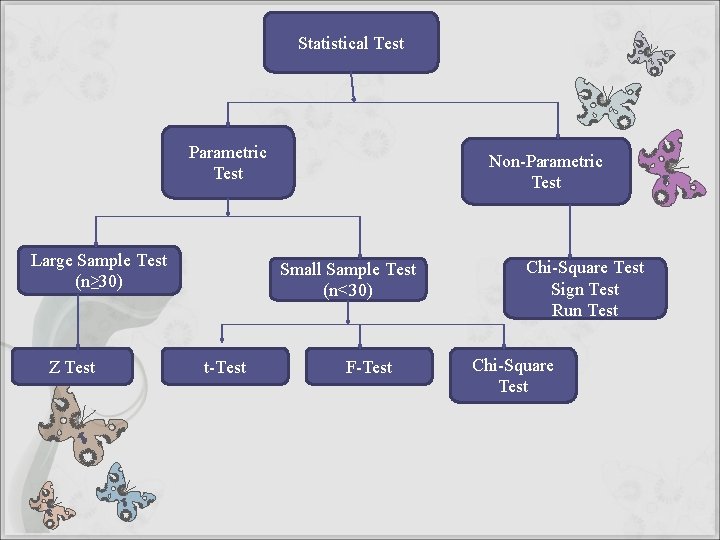
Statistical Test Parametric Test Large Sample Test (n≥ 30) Z Test Non-Parametric Test Small Sample Test (n<30) t-Test F-Test Chi-Square Test Sign Test Run Test Chi-Square Test

5) Critical Region/ Table Value The range of variation has two regions acceptance region and rejection region(critical Region).

6) Inference The decision of the basis of computed value whether it lies in the acceptance region or rejection region. If CV>TV Reject the NH If CV< TV Accept the NH

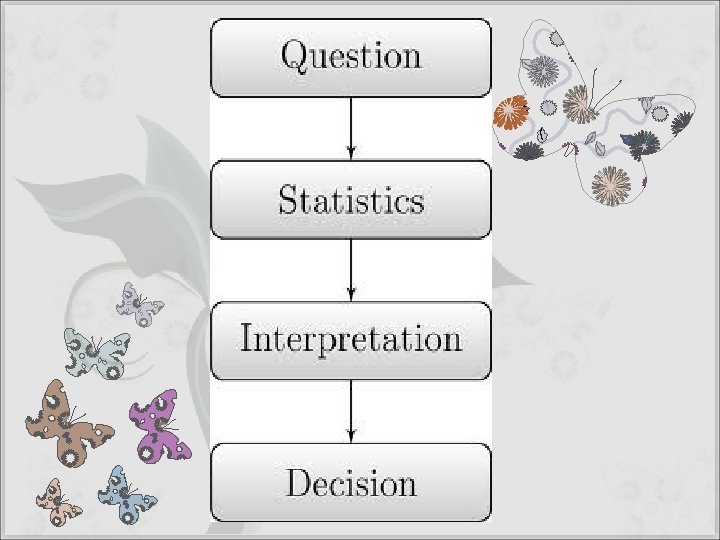
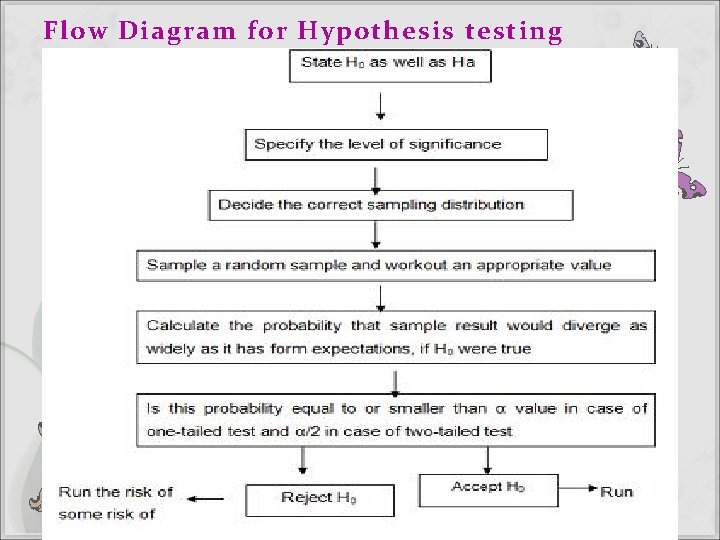
Flow Diagram for Hypothesis testing

THANK YOU