7 RANTAI MARKOV WAKTU KONTINU KelahiranKematian Murni Prostok7






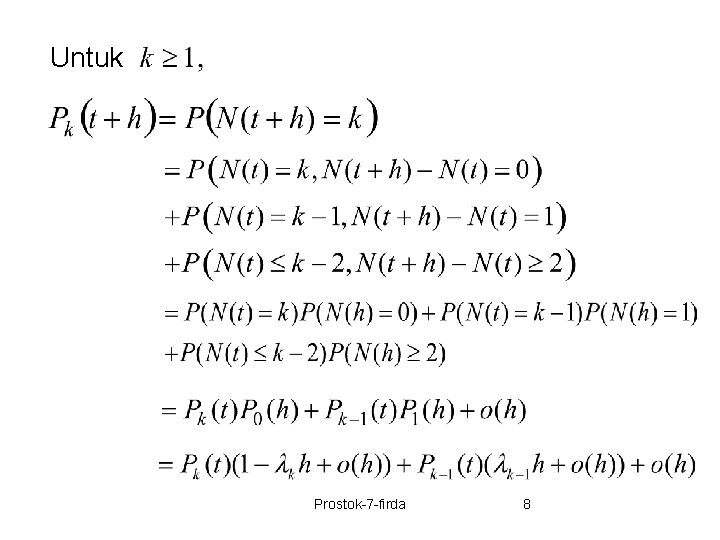










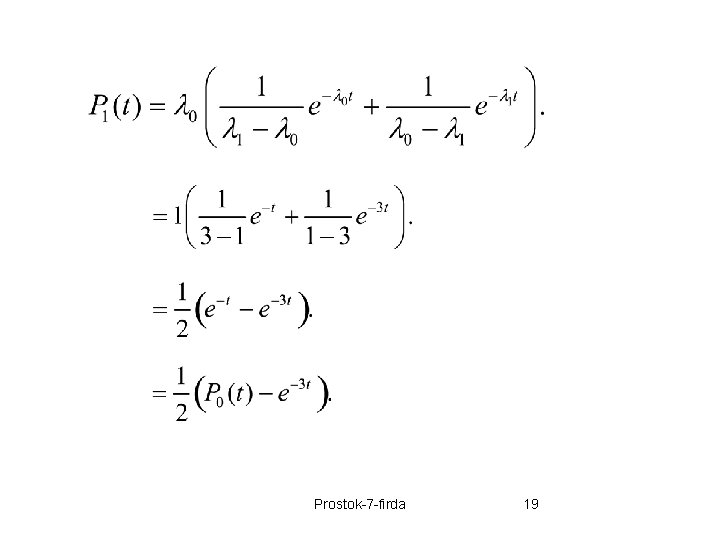





































- Slides: 59

7. RANTAI MARKOV WAKTU KONTINU (Kelahiran&Kematian Murni) Prostok-7 -firda 1

Definisi Misal proses stokastik dengan waktu kontinu dan ruang keadaan diskrit Jika untuk maka proses disebut rantai Markov waktu kontinu. Prostok-7 -firda 2

7. 1 Proses Kelahiran Murni Definisi 1 (Shunji Osaki) Jika proses menghitung adalah rantai Markov dengan peluang transisi stasioner dan memenuhi: maka proses dinamakan proses kelahiran murni dengan parameter Prostok-7 -firda 3

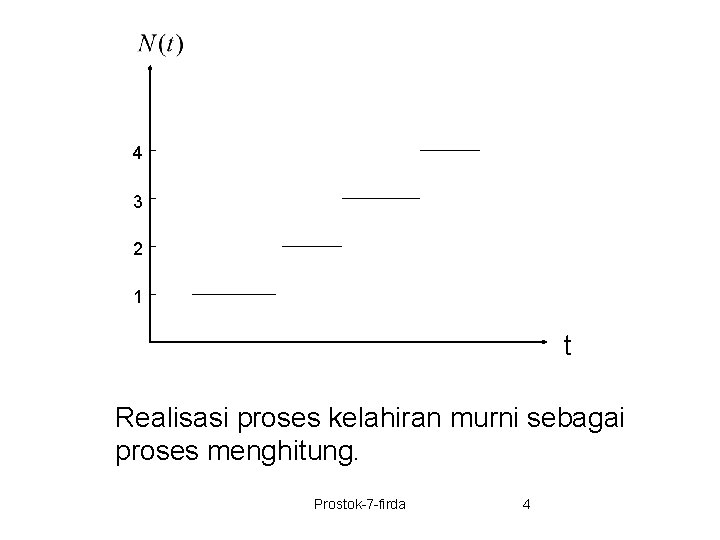
4 3 2 1 t Realisasi proses kelahiran murni sebagai proses menghitung. Prostok-7 -firda 4

Tulis peluang transisi stasioner: merupakan peluang transisi dari state i ke state j. Dengan kondisi awal (menyatakan peluang bahwa ada k kejadian yang terjadi pada interval (0, t]. Prostok-7 -firda 5

Untuk k = 0, kenaikan bebas kenaikan stasioner Sifat (2), (3) Prostok-7 -firda 6

Dari bentuk diperoleh : Dengan syarat awal Prostok-7 -firda 7
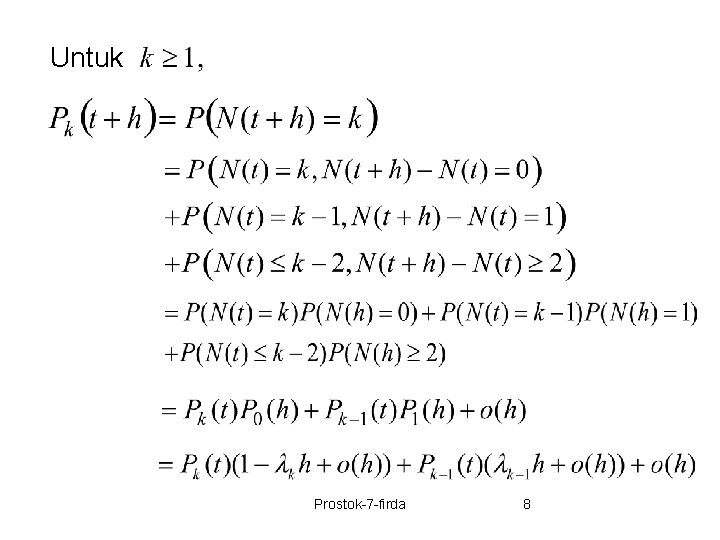
Untuk Prostok-7 -firda 8

atau Dari sini diperoleh : PDB linear Atau ditulis, (*) Prostok-7 -firda 9

Jika maka persamaan (*) memberikan hasil (1) (2) (3) dimana Prostok-7 -firda 10

Prostok-7 -firda 11

Teorema 1 Untuk proses kelahiran murni dengan parameter Waktu antar kedatangan (waktu antar kelahiran) saling bebas dan berdistribusi eksponensial dengan parameter Prostok-7 -firda 12

Teorema 2 Untuk proses kelahiran murni parameter dengan jika dan hanya jika Prostok-7 -firda 13

7. 2 Contoh Proses Kelahiran Murni 1. Proses Poisson yang mempunyai laju kelahiran konstan, Dalam hal ini, dimana, Prostok-7 -firda 14

Contoh Pada kantor catatan sipil, pengeluaran akte kelahiran mengikuti proses Poisson dengan laju 5, 5 akte/jam. Tentukan: a. Peluang tidak ada akte yang dikeluarkan dalam 1 jam. b. Jika dalam periode 3 jam dikeluarkan 35 akte, tentukan peluang pengeluaran akte pada 1 jam terakhir jika telah dikeluarkan 25 akte pada 2 jam pertama. c. Tentukan peluang bahwa selang waktu antara pengeluaran akte ke 4 dan akte ke 5 tidak lebih dari ½ jam. Prostok-7 -firda 15

Misal Jumlah akte yang dikeluarkan dalam waktu t. a. Peluang tidak akte yang dikeluarkan dalam 1 jam. b. Prostok-7 -firda 16

c. Jika waktu antar pengeluaran akte = X(t) Prostok-7 -firda 17

Contoh Sebuah proses kelahiran murni dengan N(0)=0 yang mempunyai parameter Tentukan Jawab: Untuk k=0, 1, gunakan persamaan (1), (2) slide 12. Prostok-7 -firda 18
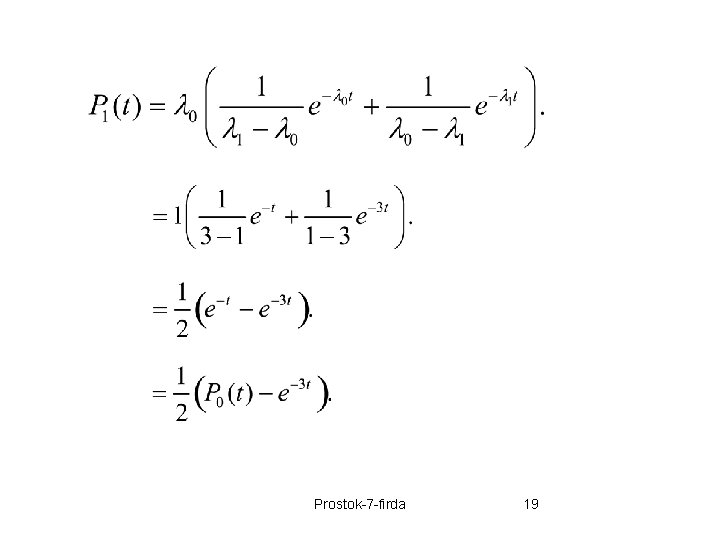
Prostok-7 -firda 19

Untuk k=2, gunakan persamaan (3) slide 12, dimana Prostok-7 -firda 20

Sehingga, Prostok-7 -firda 21

2. Proses Yule Jika menyatakan jumlah populasi pada saat t, maka adalah proses kelahiran murni dengan laju Prostok-7 -firda 22

Soal latihan 1. Sebuah proses kelahiran murni dengan N(0)=0 yang mempunyai parameter Tentukan Prostok-7 -firda 23

2. Sebuah proses Yule dengan imigrasi yang mempunyai parameter kelahiran untuk k=0, 1, 2, … dimana merupakan kelajuan imigrasi dalam populasi dan β sebagai kelajuan kelahiran individu. Asumsikan bahwa N(0)=0, Tentukan Prostok-7 -firda 24

Contoh Proses Kelahiran Murni Kelahiran bayi mengikuti distribusi eksponensial dengan rata-rata satu kelahiran 12 menit. Tentukan : a) Rata-rata kelahiran per tahun. b) Peluang tidak adanya kelahiran dalam satu hari. c) Peluang pengeluaran 50 akte kelahiran diakhir periode yang terdiri dari 3 jam dengan diketahui bahwa 40 akte dikeluarkan dalam 2 jam pertama. d) Asumsikan pegawai memasukkan data akte kelahiran ke komputer setelah terkumpul 5 akte kelahiran. Berapa peluang pegawai akan memasukkan sekumpulan data baru setiap jam. Prostok-7 -firda 25

Jawab : Misal menyatakan banyaknya kelahiran. menyatakan waktu antar kelahiran. a) rata-rata kelahiran per tahun kelahiran per hari. Jadi rata-rata kelahiran bayi 43. 800 26 bayi/tahun. Prostok-7 -firda

b) Peluang tidak ada kelahiran perhari Jadi dalam satu hari mustahil tidak ada kelahiran. Prostok-7 -firda 27

c) Peluang pengeluaran 50 akte di akhir periode (3 jam), dengan diketahui ada 40 akte di 2 jam pertama. Jadi pengeluaran 10 akte pada 1 jam terakhir kira 1, 8%. Prostok-7 -firda 28

d) Jika data akte di entri setelah terkumpul 5 data akte, berapa peluang pegawai akan mengentri sekumpulan data baru setiap jam? Minimal 5 data akte k=0, 1, 2, 3, 4, 5 Jadi kemungkinan pegawai akan mengentri setiap jam setelah terkumpul paling sedikit 5 data akte adalah 60%. Prostok-7 -firda 29

7. 3 Proses Kematian Murni Definisi 1 (Shunji Osaki) Jika proses stokastik adalah rantai Markov dengan peluang transisi stasioner, ruang keadaan , memenuhi: maka proses dinamakan proses kematian murni dengan parameter Prostok-7 -firda 30

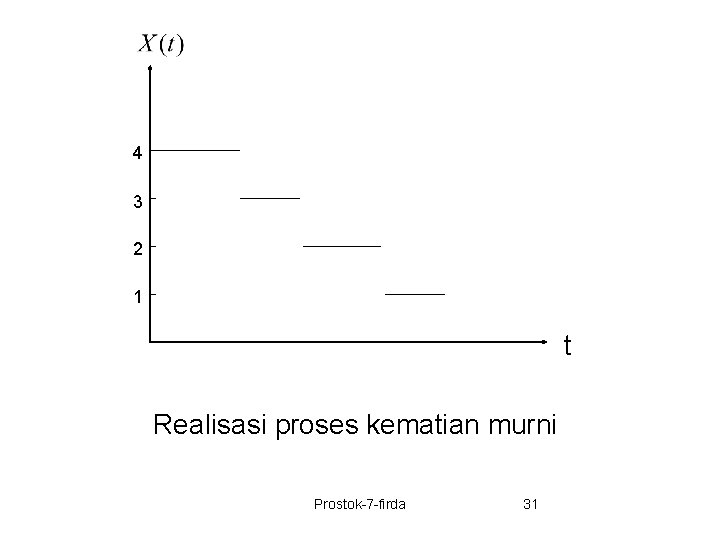
4 3 2 1 t Realisasi proses kematian murni Prostok-7 -firda 31

Tulis peluang transisi dengan kondisi awal (menyatakan peluang bahwa ada k unit yang tersisa pada interval (0, t]. Seperti proses kelahiran murni, dengan persamaan Kolmogorov diperoleh: Prostok-7 -firda 32

Khusus jika dan Prostok-7 -firda 33

Jika parameter kematian artinya berbeda untuk setiap k, Untuk dimana Prostok-7 -firda 34

7. 4 Contoh Kematian Murni 1. Sebuah toko bunga memiliki persediaan 18 lusin bunga mawar setiap awal pekan, rata-rata toko tersebut menjual 3 lusin mawar per hari, dengan permintaan yang mengikuti distribusi Poisson. Ketika persediaan mencapai 5 lusin, pesanan baru akan ditempatkan di awal pekan selanjutnya. Semua mawar yang tersisa di akhir pekan akan dibuang. Prostok-7 -firda 35

• Tentukan: a) Peluang mawar yang tersisa paling banyak 5 lusin. b) Peluang persediaan habis dalam waktu 3 hari c) Rata-rata (lusin) mawar yang tersisa di akhir hari kedua d) Peluang tidak ada mawar yang terjual selama hari pertama Prostok-7 -firda 36

Jawab: banyak mawar di awal pekan = 18 lusin laju permintaan = 3 per hari • Peluang n unit yang tersisa selama periode t : Prostok-7 -firda 37

a) Peluang mawar tersisa paling banyak 5 lusin Prostok-7 -firda 38

Prostok-7 -firda 39

b) Peluang persediaan habis dalam waktu 3 hari Jadi, peluang persediaan habis dalam 3 hari 40 adalah 0, 00608

c) Rata-rata (lusin) mawar yang tersisa di akhir hari kedua Tabel berikut meringkas perhitungan dengan diketahui µt=6 n 0 1 Pn(2) 3, 932 x 10 -5 1, 1796 x 10 -4 … 18 2, 4787 x 10 -3 Jadi, rata-rata kurang dari 12 lusin mawar yang tersisa di akhir hari kedua Prostok-7 -firda 41

d) Peluang tidak ada mawar yang terjual pada hari pertama Jadi, peluang tidak ada mawar yang terjual pada hari pertama adalah 0, 049 (4, 9%). Prostok-7 -firda 42

Contoh Proses Kematian Murni 2. Suatu proses kematian murni dimulai dari X(0)=3, dengan parameter kematian Tentukan Prostok-7 -firda 43

Jawab: Ø untuk n=0, dimana: Prostok-7 -firda 44

Jadi Prostok-7 -firda 45

Ø untuk n=1, dimana: Prostok-7 -firda 46

Jadi Prostok-7 -firda 47

Ø untuk n=2, dimana: Prostok-7 -firda 48

Jadi Ø untuk n=3, Prostok-7 -firda 49

PROSES KELAHIRAN DAN KEMATIAN Definisi (Shunji Osaki) Jika proses stokastik adalah rantai Markov dengan peluang transisi stasioner , dan memenuhi: maka proses dinamakan proses kelahiran dan kematian dengan parameter 50

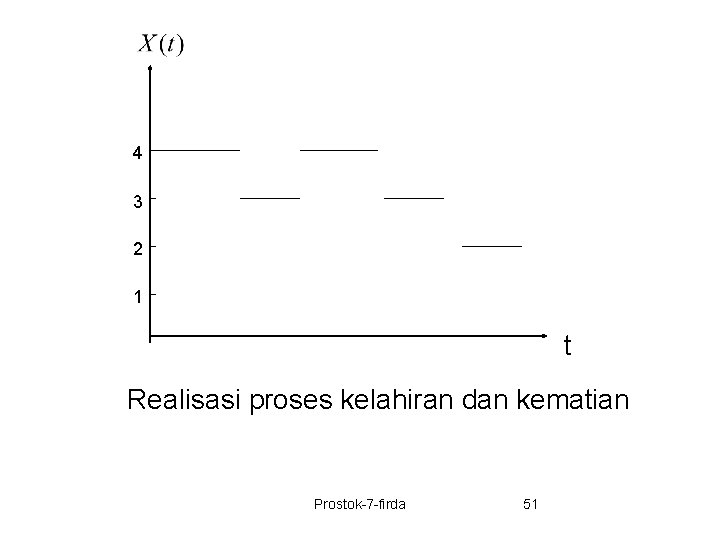
4 3 2 1 t Realisasi proses kelahiran dan kematian Prostok-7 -firda 51

Misal merupakan peluang transisi dari state i ke state j. Dengan menggunakan persamaan Chapman-Kolmogorov Prostok-7 -firda 52

Dengan menyusun ruas kiri dan kanan serta mengambil h 0 diperoleh Secara umum 53

o(h) j+1 j j i j-1 o(h) 0 t t+h Dengan menyusun ruas kiri dan kanan serta mengambil h 0 diperoleh Prostok-7 -firda 54

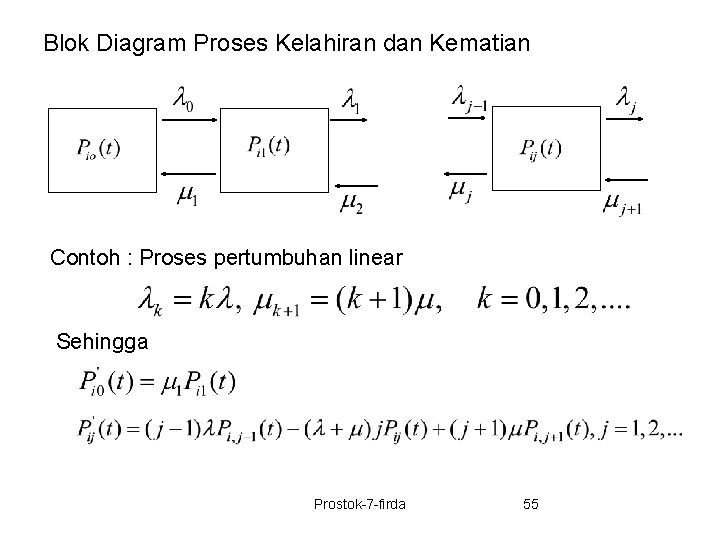
Blok Diagram Proses Kelahiran dan Kematian Contoh : Proses pertumbuhan linear Sehingga Prostok-7 -firda 55

Nilai rata-rata pada saat t dan dijumlahkan terhadap j diperoleh (*) Dengan nilai awal M(0) = i , dgn asumsi X(0) = i 56

Bukti (*) dan dijumlahkan terhadap j diperoleh Nyatakan suku pertama dalam Pij(t) Prostok-7 -firda 57

Nyatakan suku ketiga dalam Pij(t) sehingga atau 58

Distribusi Prostok-7 -firda 59