7 Queue ADTs Queue concepts Queue applications A

7 Queue ADTs • Queue concepts. • Queue applications. • A queue ADT: requirements, contract. • Implementations of queues: using arrays, linked lists. • Queues in the Java class library. © 2001, D. A. Watt and D. F. Brown

Queue concepts • A queue is a first-in-first-out sequence of elements. Elements can added only at one end (the rear of the queue) and removed only at the other end (the front of the queue). • The length of a queue is the number of elements it contains. • An empty queue has length zero.

Queue concepts (continued) • Illustration (queue of persons): BUS STOP

Queue applications • Print server § maintains a queue of print jobs. • Disk driver § maintains a queue of disk input/output requests. • Scheduler (e. g. , in an operating system) § maintains a queue of processes awaiting a slice of machine time.

Example 1: demerging (1) • Consider a file of person records, each of which contains a person’s name, gender, date of birth, etc. The records are sorted by date of birth. We are required to rearrange the records such that females precede males but they remain sorted by date of birth within each gender group. • Bad idea: use a sorting algorithm. Time complexity is O(n log n) at best. • Good idea: use a demerging algorithm. Time complexity is O(n).

Example 1 (2) • Demerging algorithm: To rearrange a file of person records such that females precede males but their order is otherwise unchanged: 1. 2. 3. 4. 5. Make queues females and males empty. Until the input file is empty, repeat: 2. 1. Let p be the next person read in from the file. 2. 2. If p is female, add p to the rear of females. 2. 3. If p is male, add p to the rear of males. Until females is empty, repeat: 3. 1. Write out the person removed from the front of females. Until males is empty, repeat: 4. 1. Write out the person removed from the front of males. Terminate.

Queue ADT: requirements • Requirements: 1) It must be possible to make a queue empty. 2) It must be possible to test whether a queue is empty. 3) It must be possible to obtain the length of a queue. 4) It must be possible to add an element at the rear of a queue. 5) It must be possible to remove the front element from a queue. 6) It must be possible to access the front element in a queue without removing it.

Queue ADT: contract (1) • Possible contract, expressed as a Java interface: public interface Queue { // Each Queue object is a queue whose elements are objects. //////// Accessors //////// public boolean is. Empty (); // Return true if and only if this queue is empty. public int size (); // Return this queue’s length. public Object get. First (); // Return the element at the front of this queue.

Queue ADT: contract (2) • Possible contract (continued): //////// Transformers //////// public void clear (); // Make this queue empty. public void add. Last (Object elem); // Add elem as the rear element of this queue. public Object remove. First (); // Remove and return the front element of this queue. }

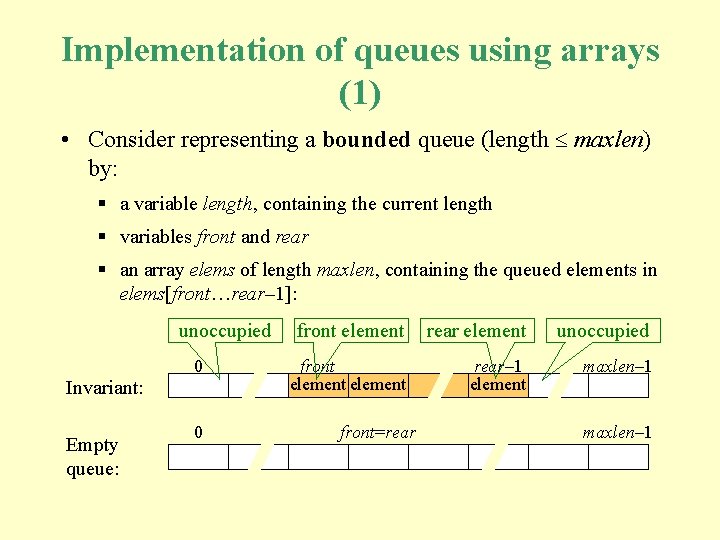
Implementation of queues using arrays (1) • Consider representing a bounded queue (length maxlen) by: § a variable length, containing the current length § variables front and rear § an array elems of length maxlen, containing the queued elements in elems[front…rear– 1]: unoccupied 0 Invariant: Empty queue: 0 front element rear element unoccupied front element rear– 1 element maxlen– 1 front=rear maxlen– 1

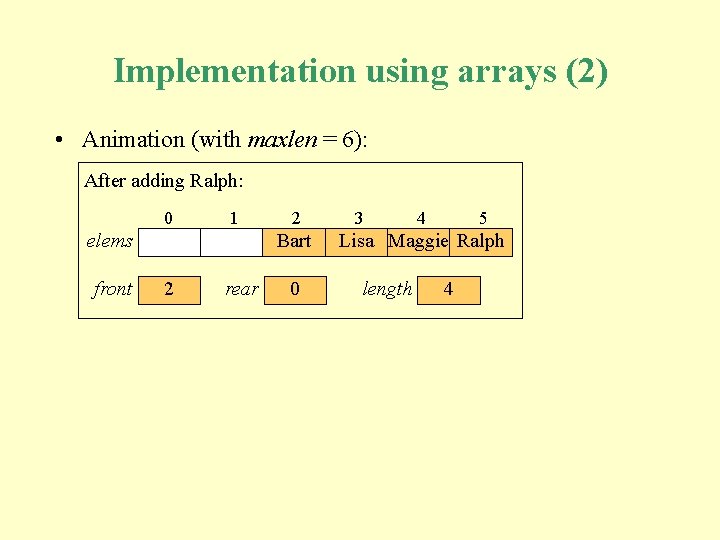
Implementation using arrays (2) • Animation (with maxlen = 6): After Initially: removing adding Maggie: Ralph: Homer, the front Marge, element: Bart, Lisa: 0 1 2 elems Homer Marge Bart front 210 rear 054 3 4 5 Lisa Maggie Ralph length 4035

Implementation using arrays (3) • If we must shift elements along the array, operations add. Last and remove. First will have time complexity O(n). • We can avoid this if we use a “cyclic array” instead of an ordinary array.

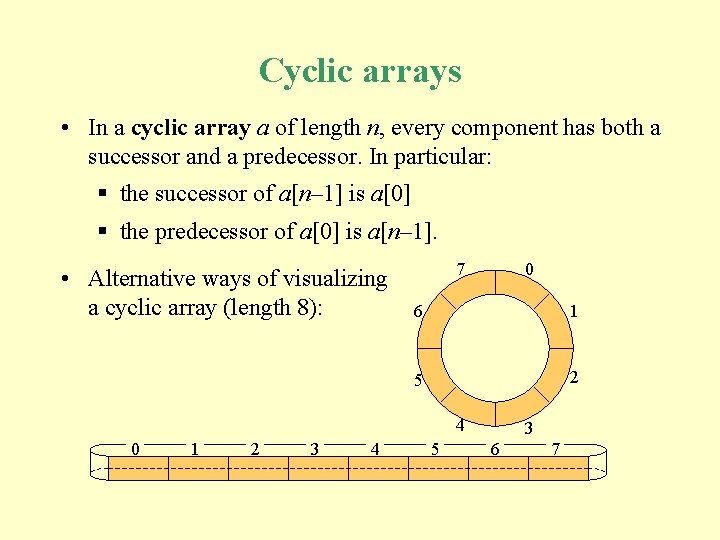
Cyclic arrays • In a cyclic array a of length n, every component has both a successor and a predecessor. In particular: § the successor of a[n– 1] is a[0] § the predecessor of a[0] is a[n– 1]. • Alternative ways of visualizing a cyclic array (length 8): 7 0 6 1 5 2 4 0 1 2 3 4 5 3 6 7

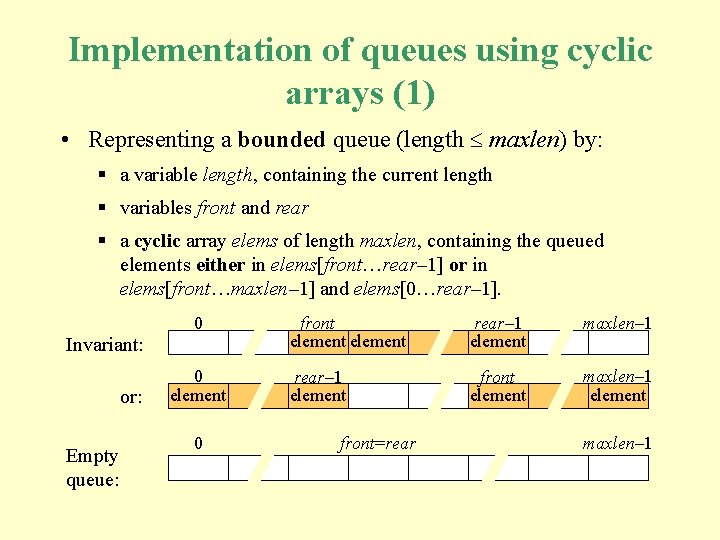
Implementation of queues using cyclic arrays (1) • Representing a bounded queue (length maxlen) by: § a variable length, containing the current length § variables front and rear § a cyclic array elems of length maxlen, containing the queued elements either in elems[front…rear– 1] or in elems[front…maxlen– 1] and elems[0…rear– 1]. 0 Invariant: or: Empty queue: 0 element 0 front element rear– 1 element maxlen– 1 rear– 1 element front element maxlen– 1 element front=rear maxlen– 1

Implementation using cyclic arrays (2) • Animation (with maxlen = 6): After Initially: adding Martin: removing Maggie: Ralph: Nelson: Homer, the front Marge, element: Bart, Lisa: 0 1 2 Homer Martin elems Nelson Marge Bart front 3210 rear 21504 3 4 5 Lisa Maggie Ralph length 54063

Implementation using cyclic arrays (3) • Java implementation: public class Array. Queue implements Queue { private Object[] elems; private int front, rear, length; //////// Constructor //////// public Array. Queue (int max. Length) { elems = new Object[max. Length]; front = rear = length = 0; }

Implementation using cyclic arrays (4) • Java implementation (continued): //////// Accessors //////// public boolean is. Empty () { return (length == 0); } public int size () { return length; } public Object get. First () { if (length == 0) throw …; return elems[front]; }

Implementation using cyclic arrays (5) • Java implementation (continued): //////// Transformers //////// public void clear () { for (int i = 0; i < elems. length; i++) elems[i] = null; front = rear = length = 0; } public void add. Last (Object elem) { if (length == elems. length) throw …; elems[rear++] = elem; if (rear == elems. length) rear = 0; length++; }

Implementation using cyclic arrays (6) • Java implementation (continued): public Object remove. First () { if (length == 0) throw …; Object front. Elem = elems[front]; elems[front++] = null; if (front == elems. length) front = 0; return front. Elem; } } • Analysis: § Most operations have time complexity O(1). § Operation clear has time complexity O(maxlen).

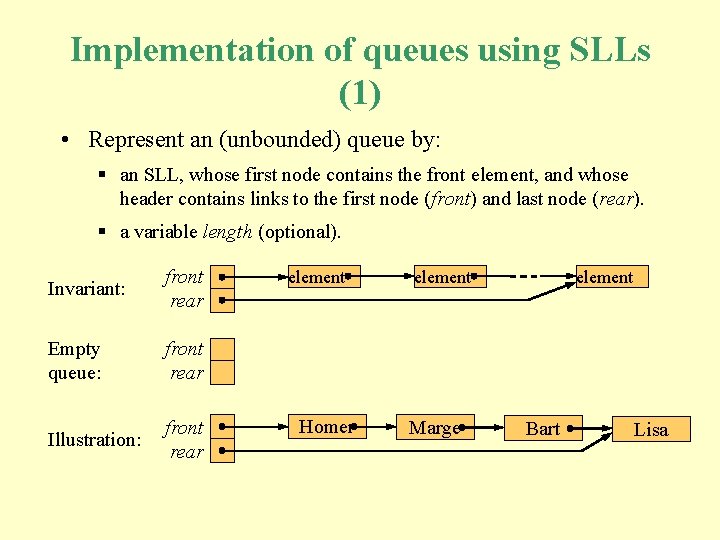
Implementation of queues using SLLs (1) • Represent an (unbounded) queue by: § an SLL, whose first node contains the front element, and whose header contains links to the first node (front) and last node (rear). § a variable length (optional). Invariant: front rear Empty queue: front rear Illustration: front rear element Homer element Marge element Bart Lisa

Implementation using SLLs (2) • Java implementation: public class Linked. Queue implements Queue { private SLLNode front, rear; //////// Constructor //////// public Linked. Queue () { front = rear = null; } //////// Accessors //////// public boolean is. Empty () { return (front == null); }

Implementation using SLLs (3) • Java implementation (continued): public int size () { int length = 0; for (SLLNode curr = front; curr != null; curr = curr. succ) length++; return length; } public Object get. First () { if (front == null) throw …; return front. element; }

Implementation using SLLs (4) • Java implementation (continued): //////// Transformers //////// public void clear () { front = rear = null; } public void add. Last (Object elem) { SLLNode newest = new SLLNode(elem, null); if (rear != null) rear. succ = newest; else front = newest; rear = newest; }

Implementation using SLLs (5) • Java implementation (continued): public Object remove. First () { if (front == null) throw …; Object front. Elem = front. element; front = front. succ; if (front == null) rear = null; return front. Elem; } } • Analysis: § Most operations have time complexity O(1), but size is O(n). § However, size too would be O(1) if we used a variable length.

Queues in the Java class library • Java provides no Queue interface or class as such. • However, the java. util. Linked. List class provides all the above Queue operations. • Illustration: import java. util. Linked. List; Linked. List queue = new Linked. List(); queue. add. Last("Homer"); queue. add. Last("Marge"); queue. add. Last("Bart"); queue. add. Last("Lisa"); queue. add. Last("Maggie"); System. out. println(bus. Queue. remove. First());

Example 2: demerging revisited (1) • Recall the demerging algorithm of Example 1. • Implementation: public static void re. Sort. Persons ( Buffered. Reader input, Buffered. Writer output) throws IOException { Linked. List female. Queue = new Linked. List(); Linked. List male. Queue = new Linked. List(); for (; ; ) { Person p = read. Person(input); if (p == null) break; // end of input if (p. female)

Example 2 (2) • Implementation (continued): while (! female. Queue. is. Empty()) { Person f = female. Queue. remove. First(); write. Person(output, f); } while (! male. Queue. is. Empty()) { Person m = male. Queue. remove. First(); write. Person(output, m); } }