7 Estimating a Parameter Lesson 7 5 Estimating

7 Estimating a Parameter Lesson 7. 5 Estimating a Mean Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Estimating a Mean Learning Targets After this lesson, you should be able to: ü State and check the Random and Normal/Large Sample conditions for constructing a confidence interval for a population mean. ü Determine critical values for calculating a C% confidence interval for a population mean. ü Calculate a C% confidence interval for a population mean. Statistics and Probability with Applications, 3 rd Edition 2

Estimating a Mean Like confidence intervals for a population proportion, there are conditions that need to be met to construct a confidence interval for a population mean. How to Check the Conditions for Constructing a Confidence Interval for µ • Random: The data come from a random sample from the population of interest. • Normal/Large Sample: The data come from a normally distributed population or the sample size is large (n ≥ 30). When the Random condition is satisfied, we can generalize about the population from which the sample was selected. We check the Normal/Large Sample condition to make sure the distribution of is approximately normal. Statistics and Probability with Applications, 3 rd Edition 3

Did you blow a gasket? Checking conditions PROBLEM: A particular machine manufactures rubber gaskets with outside diameters that vary according to a normal distribution. To estimate the mean outside diameter of all gaskets produced by this machine during a production run, a quality control engineer randomly selects 10 gaskets. Are the conditions met for calculating a confidence interval for µ? Justify. Random? • Random sample of gaskets from the production run. Normal/Large Sample? • The sample size is not large: n = 10 < 30, but we know that the population follows a normal distribution. Statistics and Probability with Applications, 3 rd Edition 4

Estimating a Mean Confidence intervals are made up of two parts, the point estimate and the margin of error: point estimate ± margin of error The confidence interval for a population mean is: Unfortunately, if we don’t know the true value of µ, we rarely know the true value of �� either. We can use sx as an estimate for ��, but things don’t work out as nicely as we might like. Statistics and Probability with Applications, 3 rd Edition 5

Activity Confidence Interval BINGO! • Statistics and Probability with Applications, 3 rd Edition 6

Activity Confidence Interval BINGO! • Statistics and Probability with Applications, 3 rd Edition 7

Activity Confidence Interval BINGO! • Statistics and Probability with Applications, 3 rd Edition 8

Activity Confidence Interval BINGO! • Statistics and Probability with Applications, 3 rd Edition 9

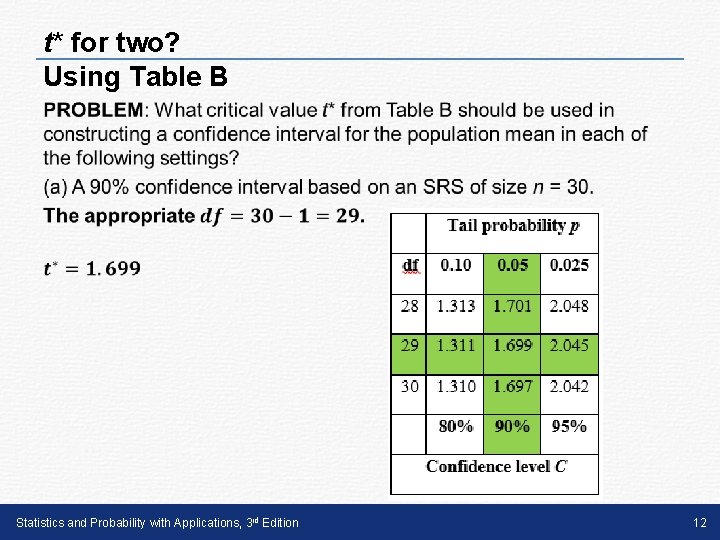
Estimating a Mean When calculating a confidence interval for a population mean, we use a t* critical value rather than a z* critical value whenever we use sx to estimate ��. How to Find t* 1. Using Table B, find the correct confidence level at the bottom of the table. 2. On the left side of the table, find the correct number of degrees of freedom (df ). For this type of confidence interval, df = n - 1. 3. In the body of the table, find the value of t* that corresponds to the confidence level and df. 4. If the correct df isn’t listed, use the greatest df available that is less than the correct df. Statistics and Probability with Applications, 3 rd Edition 10

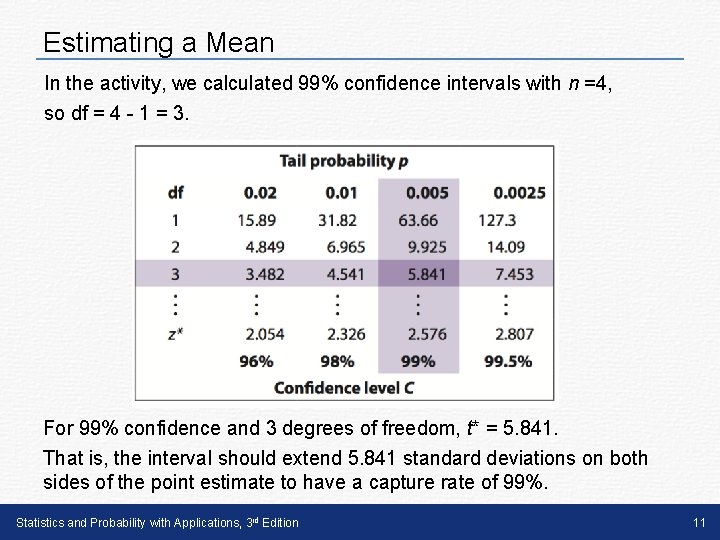
Estimating a Mean In the activity, we calculated 99% confidence intervals with n =4, so df = 4 - 1 = 3. For 99% confidence and 3 degrees of freedom, t* = 5. 841. That is, the interval should extend 5. 841 standard deviations on both sides of the point estimate to have a capture rate of 99%. Statistics and Probability with Applications, 3 rd Edition 11

t* for two? Using Table B • Statistics and Probability with Applications, 3 rd Edition 12

t* for two? Using Table B • Statistics and Probability with Applications, 3 rd Edition 13

Estimating a Mean Because we almost never know the population standard deviation ��, we must use the sample standard deviation sx as an estimate for ��. This means that we must estimate the standard deviation_ of the sampling _ distribution of x with the standard error of x. _ Standard error of x _ The standard error of x_ is an estimate of the standard deviation of the sampling distribution of x. _ _ The standard error of x estimates how much x typically varies from µ. Statistics and Probability with Applications, 3 rd Edition 14

Estimating a Mean How to Calculate a Confidence Interval for µ When the Random and Normal/Large Sample conditions are met, a C% confidence interval for the unknown mean µ is where t* is the critical value for a t distribution with df = n - 1 and C% of its area between -t* and t*. Statistics and Probability with Applications, 3 rd Edition 15

Is this gasket just right? Calculating a confidence interval for µ • Statistics and Probability with Applications, 3 rd Edition 16

LESSON APP 7. 5 What does an Oreo weigh? For their second-semester project, Ann and Tori wanted to estimate the average weight of an Oreo cookie to determine if the average weight was less than advertised. They selected a random sample of 36 cookies and_found the weight of each cookie (in grams). The mean weight was x =11. 3921 grams, with a standard deviation of sx =0. 0817 grams. 1. Verify that the conditions are met for constructing a confidence interval for µ. 2. Construct a 95% confidence interval for µ. 3. On the packaging, the stated serving size is 3 cookies (34 grams). Does the interval in Question 2 provide convincing evidence that the average weight of an Oreo cookie is less than advertised? Explain. Statistics and Probability with Applications, 3 rd Edition 17

LESSON APP 7. 5 What does an Oreo weigh? 1. Verify that the conditions are met for constructing a confidence interval for µ. 2. Construct a 95% confidence interval for µ. Statistics and Probability with Applications, 3 rd Edition 18

LESSON APP 7. 5 What does an Oreo weigh? 3. On the packaging, the stated serving size is 3 cookies (34 grams). Does the interval in Question 2 provide convincing evidence that the average weight of an Oreo cookie is less than advertised? Explain. Statistics and Probability with Applications, 3 rd Edition 19

Estimating a Mean Learning Targets After this lesson, you should be able to: ü State and check the Random and Normal/Large Sample conditions for constructing a confidence interval for a population mean. ü Determine critical values for calculating a C% confidence interval for a population mean. ü Calculate a C% confidence interval for a population mean. Statistics and Probability with Applications, 3 rd Edition 20