7 Assignment Problem n resources n activities Note

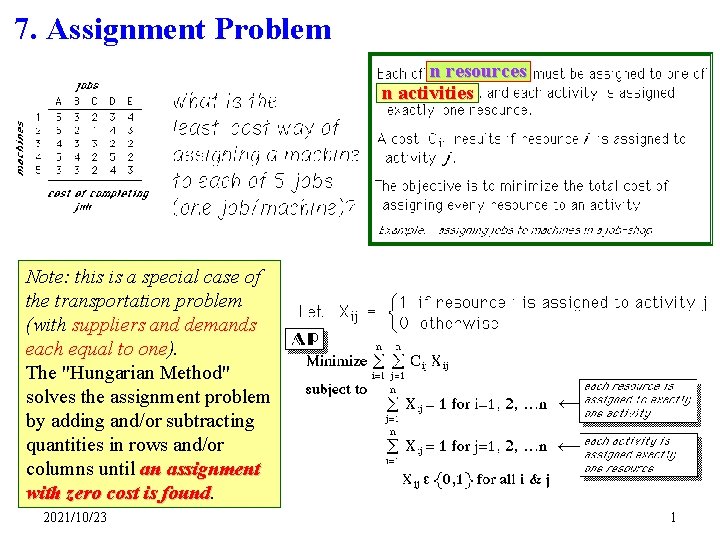
7. Assignment Problem n resources n activities Note: this is a special case of the transportation problem (with suppliers and demands each equal to one). The "Hungarian Method" solves the assignment problem by adding and/or subtracting quantities in rows and/or columns until an assignment with zero cost is found 2021/10/23 1

7. 1 Assignment Problem example 6 4 Min. 6 X 11+4 X 12+5 X 13+5 X 14 +7 X 21+4 X 22+5 X 23+6 X 24 +4 X 31+7 X 32+6 X 33+4 X 34 +5 X 41+3 X 42+4 X 43+7 X 44 2021/10/23 St. X 11+X 12+X 13+X 14=1 X 21+X 22+X 23+X 24=1 X 31+X 32+X 33+X 34=1 X 41+X 42+X 43+X 44=1 X 11+X 21+X 31+X 41=1 X 12+X 22+X 32+X 42=1 X 13+X 23+X 33+X 43=1 X 14+X 24+X 34+X 44=1 2

7. 2 Hungarian Algorithm STEP 0 Convert to standard form, with # rows = # columns (即必要時加slack) STEP 1 Row reduction: find the smallest cost in each row, and reduce all costs in the row by this amount. (機會成本概念) STEP 2 Column reduction: find the smallest cost in each column, and reduce all costs in the column by this amount. STEP 3 Find the minimum number of lines through rows &/or columns (至少 須有一條方向不同的line) necessary to cover all of the zeroes in the cost matrix. If this equals n, then STOP. (Zero assignment) STEP 4 Locate the smallest unlined cost. Subtract this cost from all unlined costs, and add to costs at intersections of lines. Return to step 3. 2021/10/23 3

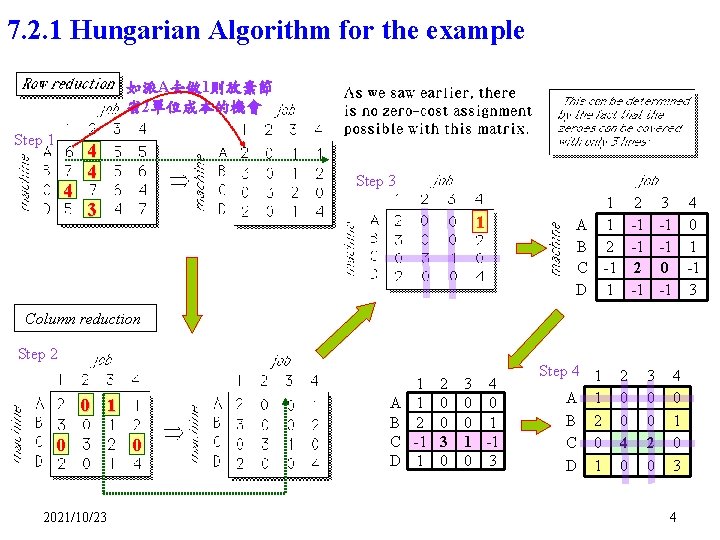
7. 2. 1 Hungarian Algorithm for the example 如派A去做 1則放棄節 省2單位成本的機會 Step 1 4 4 4 Step 3 3 1 A B C D 1 2 3 4 1 -1 -1 0 2 -1 -1 2 0 -1 1 -1 -1 3 Column reduction Step 2 0 1 0 2021/10/23 0 A B C D 1 1 2 -1 1 2 0 0 3 4 0 0 0 1 1 -1 0 3 Step 4 1 A 1 B 2 C 0 D 1 2 0 0 4 0 3 0 0 2 0 4 0 1 0 3 4

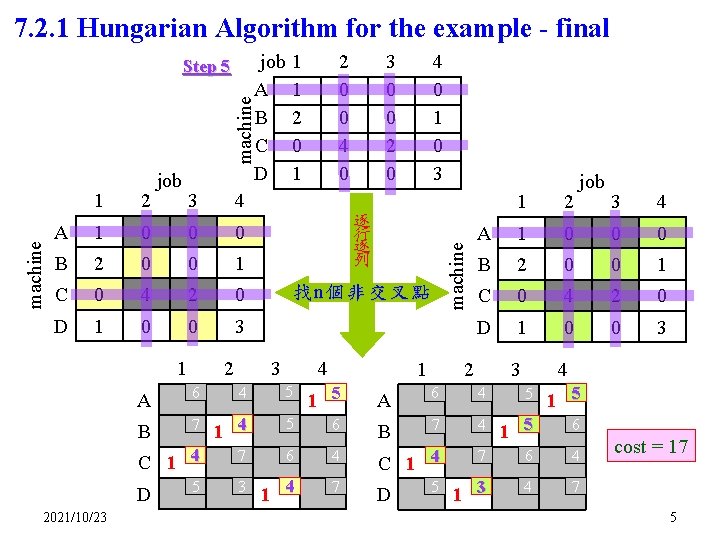
7. 2. 1 Hungarian Algorithm for the example - final machine 1 2 A 1 B job 1 1 2 0 0 4 0 3 0 0 2 0 4 0 1 0 3 3 4 0 0 0 2 0 0 1 逐 行 逐 列 C 0 4 2 0 找 n個非交叉點 D 1 0 0 3 1 3 4 1 1 2 A 1 B job 3 4 0 0 0 2 0 0 1 C 0 4 2 0 D 1 0 0 3 2 3 4 A 6 4 5 1 5 B 7 1 4 5 6 B 7 4 1 5 6 C 1 4 7 6 4 5 3 1 4 7 D 5 1 3 4 7 D 2021/10/23 2 machine job A B C D Step 5 cost = 17 5