7 8 Special Products of Binomials Lesson Objective

7 -8 Special Products of Binomials Lesson Objective: I will be able to … • Find special products of binomials Language Objective: I will be able to … • Read, write, and listen about vocabulary, key concepts, and examples Holt Algebra 1

7 -8 Special Products of Binomials Page 37 Holt Algebra 1

7 -8 Special Products of Binomials Imagine a square with sides of length (a + b): The area of this square is (a + b) or (a + b)2. The area of this square can also be found by adding the areas of the smaller squares and the rectangles inside. The sum of the areas inside is a 2 + ab + b 2. Holt Algebra 1

7 -8 Special Products of Binomials This means that (a + b)2 = a 2+ 2 ab + b 2. You can use the FOIL method to verify this: F L (a + b)2 = (a + b) = a 2 + ab + b 2 I = a 2 + 2 ab + b 2 O A trinomial of the form a 2 + 2 ab + b 2 is called a perfect-square trinomial. Page 37 A perfect-square trinomial is a trinomial that is the result of squaring a binomial. Holt Algebra 1

7 -8 Special Products of Binomials Page 38 Multiply. A. (x +3)2 Example 1: Finding Products in the Form (a + b)2 = a 2 + 2 ab + b 2 (x + 3)2 = x 2 + 2(x)(3) + 32 = x 2 + 6 x + 9 Use the rule for (a + b)2. Identify a and b: a = x and b = 3. Simplify. B. (4 s + 3 t)2 (a + b)2 = a 2 + 2 ab + b 2 Use the rule for (a + b)2. Identify a and b: a = 4 s and b = 3 t. (4 s + 3 t)2 = (4 s)2 + 2(4 s)(3 t) + (3 t)2 = 16 s 2 + 24 st + 9 t 2 Holt Algebra 1 Simplify.

7 -8 Special Products of Binomials Page 38 Your Turn 1 Multiply. (5 a + b)2 (a + b)2 = a 2 + 2 ab + b 2 Use the rule for (a + b)2. (5 a + b)2 = (5 a)2 + 2(5 a)(b) + b 2 Identify a and b: a = 5 a and b = b. Simplify. = 25 a 2 + 10 ab + b 2 Holt Algebra 1

7 -8 Special Products of Binomials You can use the FOIL method to find products in the form of (a – b)2. F L (a – b)2 = (a – b) = a 2 – ab + b 2 I O = a 2 – 2 ab + b 2 A trinomial of the form a 2 – ab + b 2 is also a perfect-square trinomial because it is the result of squaring the binomial (a – b). Holt Algebra 1

7 -8 Special Products of Binomials Page 38 Multiply. Example 2: Finding Products in the Form (a – b)2 A. (x – 6)2 (a – b)2 = a 2 – 2 ab + b 2 (x – 6)2 = x 2 – 2 x(6) + (6)2 = x 2 – 12 x + 36 Use the rule for (a – b)2. Identify a and b: a = x and b = 6. Simplify. B. (4 m – 10)2 Use the rule for (a – b)2. Identify a and b: a = 4 m (a – b)2 = a 2 – 2 ab + b 2 and b = 10. (4 m – 10)2 = (4 m)2 – 2(4 m)(10) + (10)2 = 16 m 2 – 80 m + 100 Simplify. Holt Algebra 1

7 -8 Special Products of Binomials Your Turn 2 Page 39 Multiply. (3 b – 2 c)2 (a – b) = a 2 – 2 ab + b 2 (3 b – 2 c)2 = (3 b)2 – 2(3 b)(2 c) + = 9 b 2 – 12 bc + 4 c 2 Holt Algebra 1 Use the rule for (a – b)2. (2 c)2 Identify a and b: a = 3 b and b = 2 c. Simplify.

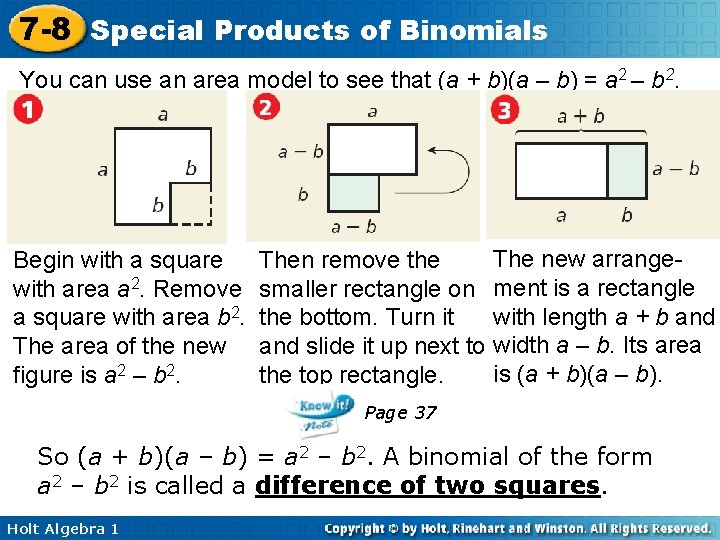
7 -8 Special Products of Binomials You can use an area model to see that (a + b)(a – b) = a 2 – b 2. Begin with a square with area a 2. Remove a square with area b 2. The area of the new figure is a 2 – b 2. Then remove the smaller rectangle on the bottom. Turn it and slide it up next to the top rectangle. The new arrangement is a rectangle with length a + b and width a – b. Its area is (a + b)(a – b). Page 37 So (a + b)(a – b) = a 2 – b 2. A binomial of the form a 2 – b 2 is called a difference of two squares. Holt Algebra 1

7 -8 Special Products of Binomials Page 39 Example 3: Finding Products in the Form (a + b)(a – b) Multiply. A. (x + 4)(x – 4) (a + b)(a – b) = a 2 – b 2 (x + 4)(x – 4) = x 2 – 42 = x 2 – 16 Use the rule for (a + b)(a – b). Identify a and b: a = x and b = 4. Simplify. B. (p 2 + 8 q)(p 2 – 8 q) Use the rule for (a + b)(a – b) = a 2 – b 2 Identify a and b: a = p 2 (p 2 + 8 q)(p 2 – 8 q) = (p 2)2 – (8 q)2 and b = 8 q. = p 4 – 64 q 2 Simplify. Holt Algebra 1

7 -8 Special Products of Binomials Page 39 Your Turn 3 Multiply. (3 + 2 y 2)(3 – 2 y 2) (a + b)(a – b) = a 2 – b 2 (3 + 2 y 2)(3 – 2 y 2) = 32 – (2 y 2)2 = 9 – 4 y 4 Holt Algebra 1 Use the rule for (a + b)(a – b). Identify a and b: a = 3 and b = 2 y 2. Simplify.

7 -8 Special Products of Binomials Classwork Assignment #7 • Holt 7 -8 #2 - 13 Holt Algebra 1