7 7 Geometric Sequences as Exponential Functions Essential

7 -7: Geometric Sequences as Exponential Functions Essential Skills: Identify and generate geometric sequences Relate geometric sequences to exponential functions

7 -7: Geometric Sequences Geometric Sequence: A pattern where the first term is not zero, and each term after the first can be found by multiplying the previous term by a common ratio. Common ratio: The number that multiplies each term in a geometric sequence.

7 -7: Geometric Sequences Example 1 A: Determine whether the sequence is arithmetic, geometric, or neither. Explain. 0, 8, 16, 24, 32, … Try subtracting consecutive numbers to see if the pattern is algebraic 8 – 0 = 8 16 – 8 = 8 24 – 16 = 8 32 – 24 = 8 The common difference is 8, so the sequence is algebraic

7 -7: Geometric Sequences Example 1 B: Determine whether the sequence is arithmetic, geometric, or neither. Explain. 64, 48, 36, 27, … Try subtracting consecutive numbers to see if the pattern is algebraic 48 – 64 = -16 36 – 48 = -12 It’s not algebraic Try dividing consecutive numbers to see if the pattern is geometric 3 48/ 64 = /4 3 36/ 48 = /4 3 27/ 36 = /4 The common ratio is ¾, so the sequence is geometric

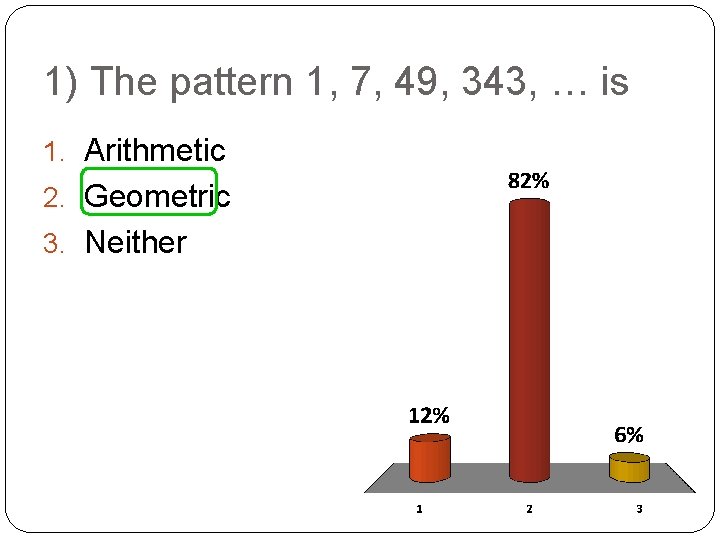
1) The pattern 1, 7, 49, 343, … is 1. Arithmetic 2. Geometric 3. Neither

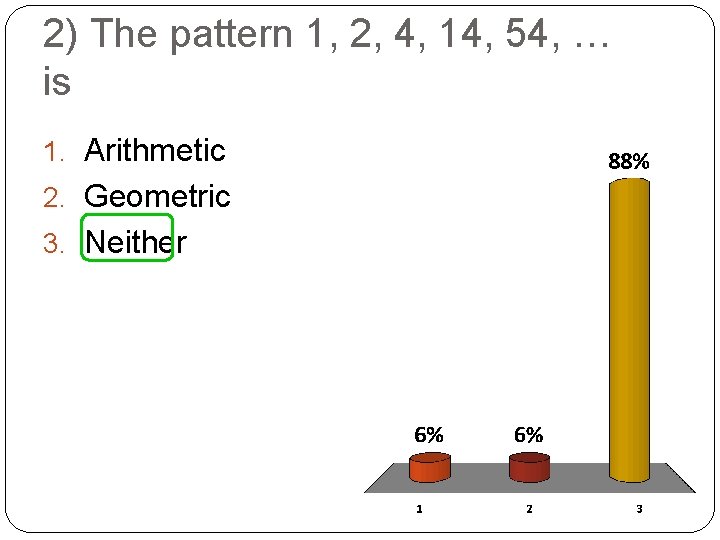
2) The pattern 1, 2, 4, 14, 54, … is 1. Arithmetic 2. Geometric 3. Neither

7 -7: Geometric Sequences Example 2 A: Find the next three terms in the geometric sequence 1, -8, 64, -512, … Step 1: Find the common ratio /1 = -8 64/ = -8 -8 -512/ 64 = -8 The common ratio is -8 Step 2: Continue the pattern with the common ratio -512 ● -8 = 4096 ● -8 = -32, 768 ● -8 = 262, 144 The next three terms are 4096, -32, 768, and 262, 144

7 -7: Geometric Sequences Example 2 B: Find the next three terms in the geometric sequence 40, 20, 10, 5, … Step 1: Find the common ratio /40 = ½ 10/ 20 = ½ 5/ 10 = ½ The common ratio is ½ 20 Step 2: Continue the pattern with the common ratio 5 ● ½ = 5 / 2 /2 ● ½ = 5/4 5/ ● ½ = 5/ 4 8 5 The next three terms are 5/2, 5/4, and 5/8

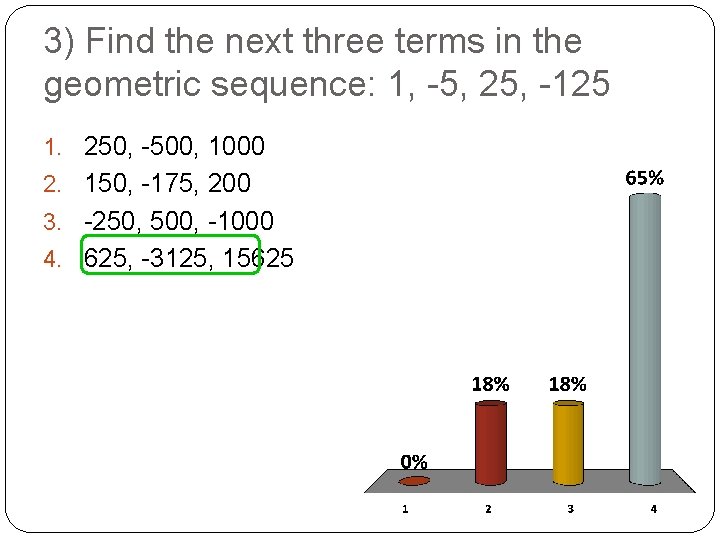
3) Find the next three terms in the geometric sequence: 1, -5, 25, -125 1. 250, -500, 1000 2. 150, -175, 200 3. -250, 500, -1000 4. 625, -3125, 15625

4) Find the next three terms in the geometric sequence: 800, 200, 50, 25/2 1. 15, 10, 5 2. 25/ 8, 25/ 32, 25/ 3. 12, 3, ¾ 4. 0, -25, -50 128

7 -7: Geometric Sequences nth term of a Geometric Sequence We can find any term in a geometric sequence if we know two things: The first term in the sequence, called a 1 The common ratio r The nth term in a sequence can then be found using the formula an = a 1 rn-1 Hint: Do the “n-1” exponent first, and

7 -7: Geometric Sequences Example 3 A: Write an equation for the nth term of a geometric sequence: 1, -2, 4, -8, … Step 1: Find the first term 1 Step 2: Find the common ratio r = -2/1 = -2 Step 3: Substitute into the equation an = a 1 rn-1 an = 1(-2)n-1 Example 3 B: Find the 12 th term of the sequence Substitute 12 for n and solve a 12 = 1(-2)12 -1 a 12 = 1(-2)11 a 12 = -2048

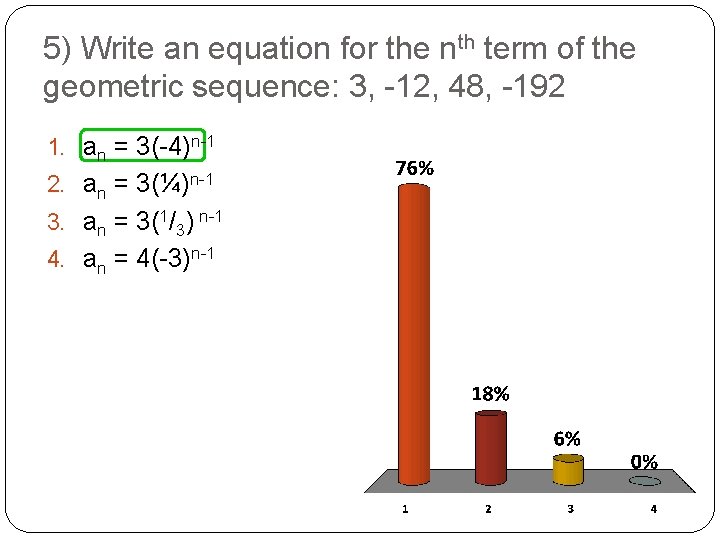
5) Write an equation for the nth term of the geometric sequence: 3, -12, 48, -192 1. an = 3(-4)n-1 2. an = 3(¼)n-1 3. an = 3(1/3) n-1 4. an = 4(-3)n-1

6) Find the 7 th term of this sequence using the equation an = 3(-4)n-1 1. 768 2. -3072 3. 12, 288 4. -49, 152

Leader Board (6 points) 6 6 Jemikah Harrell Madison Roney Daniel Helper Andrew Duncan 6 Isaiah Hanlan

7 -7: Geometric Sequences Assignment Page 441 1 – 11, 15 – 29 (odds)