7 7 Determinants Cramers Rule Section 7 7












































- Slides: 44

7. 7 Determinants. Cramer’s Rule Section 7. 7 p 1

7. 7 Determinants. Cramer’s Rule A determinant of order n is a scalar associated with an n × n (hence square!) matrix A = [ajk], and is denoted by (1) For n = 1, this determinant is defined by (2) D = a 11. Section 7. 7 p 2

7. 7 Determinants. Cramer’s Rule EXAMPLE Expansions of a Third-Order Determinant =1(12 − 0) − 3(4 + 4) + 0(0 + 6) = − 12. This is the expansion by the first row. The expansion by the third column is Verify that the other four expansions also give the value − 12. Section 7. 7 p 3

7. 7 Determinants. Cramer’s Rule General Properties of Determinants There is an attractive way of finding determinants (1) that consists of applying elementary row operations to (1). By doing so we obtain an “upper triangular” determinant (see Sec. 7. 1, for definition with “matrix” replaced by “determinant”) whose value is then very easy to compute, being just the product of its diagonal entries. This approach is similar (but not the same!) to what we did to matrices in Sec. 7. 3. In particular, be aware that interchanging two rows in a determinant introduces a multiplicative factor of − 1 to the value of the determinant! Details are as follows. Section 7. 7 p 4

7. 7 Determinants. Cramer’s Rule THEOREM 1 Behavior of an nth-Order Determinant under Elementary Row Operations (a) Interchange of two rows multiplies the value of the determinant by − 1. (b) Addition of a multiple of a row to another row does not alter the value of the determinant. (c) Multiplication of a row by a nonzero constant c multiplies the value of the determinant by c. (This holds also when c = 0, but no longer gives an elementary row operation. ) Section 7. 7 p 5

7. 7 Determinants. Cramer’s Rule EXAMPLE Evaluation of Determinants by Reduction to Triangular Form Because of Theorem 1 we may evaluate determinants by reduction to triangular form, as in the Gauss elimination for a matrix. For instance (with the blue explanations always referring to the preceding determinant) Section 7. 7 p 6

7. 7 Determinants. Cramer’s Rule EXAMPLE 4 (continued) Evaluation of Determinants by Reduction to Triangular Form (continued) Section 7. 7 p 7

7. 7 Determinants. Cramer’s Rule EXAMPLE 4 (continued) Evaluation of Determinants by Reduction to Triangular Form (continued) Section 7. 7 p 8

7. 7 Determinants. Cramer’s Rule THEOREM 2 Further Properties of nth-Order Determinants (a)–(c) in Theorem 1 hold also for columns. (d) Transposition leaves the value of a determinant unaltered. (e) A zero row or column renders the value of a determinant zero. (f ) Proportional rows or columns render the value of a determinant zero. In particular, a determinant with two identical rows or columns has the value zero. Section 7. 7 p 9

7. 7 Determinants. Cramer’s Rule THEOREM 3 Rank in Terms of Determinants Consider an m × n matrix A = [ajk]: (1) A has rank r ≥ 1 if and only if A has an r × r submatrix with a nonzero determinant. (2) The determinant of any square submatrix with more than r rows, contained in A (if such a matrix exists!) has a value equal to zero. Furthermore, if m = n, we have: (3) An n × n square matrix A has rank n if and only if det A ≠ 0. Section 7. 7 p 10

7. 7 Determinants. Cramer’s Rule THEOREM 4 Cramer’s Theorem (Solution of Linear Systems by Determinants) (a) If a linear system of n equations in the same number of unknowns x 1, … , xn (6) has a nonzero coefficient determinant D = det A, the system has precisely one solution. Section 7. 7 p 11

7. 7 Determinants. Cramer’s Rule THEOREM 4 (continued) Cramer’s Theorem (Solution of Linear Systems by Determinants) (continued) This solution is given by the formulas (7) where Dk is the determinant obtained from D by replacing in D the kth column by the column with the entries b 1, … , bn. (b) Hence if the system (6) is homogeneous and D ≠ 0, it has only the trivial solution x 1 = 0, x 2 = 0, … , xn = 0. If D = 0 the homogeneous system also has nontrivial solutions. Section 7. 7 p 12

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Section 7. 8 p 13

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination In this section we consider square matrices exclusively. The inverse of an n × n matrix A = [ajk] is denoted by A− 1 and is an n × n matrix such that (1) AA− 1 = A− 1 A = I where I is the n × n unit matrix (see Sec. 7. 2). If A has an inverse, then A is called a nonsingular matrix. If A has no inverse, then A is called a singular matrix. If A has an inverse, the inverse is unique. Indeed, if both B and C are inverses of A, then AB = I and CA = I so that we obtain the uniqueness from B = IB = (CA)B = C(AB) = CI = C. Section 7. 8 p 14

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination THEOREM 1 Existence of the Inverse The inverse A− 1 of an n × n matrix A exists if and only if rank A = n, thus (by Theorem 3, Sec. 7. 7) if and only if det A ≠ 0. Hence A is nonsingular if rank A = n and is singular if rank A < n. Section 7. 8 p 15

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Determination of the Inverse by the Gauss–Jordan Method EXAMPLE 4 Finding the Inverse of a Matrix by Gauss–Jordan Elimination Determine the inverse A− 1 of Section 7. 8 p 16

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 4 (continued) Finding the Inverse of a Matrix by Gauss–Jordan Elimination Solution. We apply the Gauss elimination (Sec. 7. 3) to the following n × 2 n = 3 × 6 matrix, where BLUE always refers to the previous matrix. Section 7. 8 p 17

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 4 (continued) Finding the Inverse of a Matrix by Gauss–Jordan Elimination Solution. (continued 1) Section 7. 8 p 18

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 4 (continued) Finding the Inverse of a Matrix by Gauss–Jordan Elimination Solution. (continued 2) This is [U H] as produced by the Gauss elimination. Now follow the additional Gauss–Jordan steps, reducing U to I, that is, to diagonal form with entries 1 on the main diagonal. Section 7. 8 p 19

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 4 (continued) Finding the Inverse of a Matrix by Gauss–Jordan Elimination Solution. (continued 3) Section 7. 8 p 20

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 4 (continued) Finding the Inverse of a Matrix by Gauss–Jordan Elimination Solution. (continued 4) The last three columns constitute A− 1. Check: Hence AA− 1 = I. Similarly A− 1 A = I. Section 7. 8 p 21

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Formulas for Inverses THEOREM 2 Inverse of a Matrix by Determinants The inverse of a nonsingular n × n matrix A = [ajk] is given by (4) where Cjk is the cofactor of ajk in det A (see Sec. 7. 7). Section 7. 8 p 22

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination THEOREM 2 (continued) Inverse of a Matrix by Determinants (continued) (CAUTION! Note well that in A− 1, the cofactor Cjk occupies the same place as akj (not ajk) does in A. ) In particular, the inverse of (4*) Section 7. 8 p 23

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 2 Inverse of a 2 × 2 Matrix by Determinants Section 7. 8 p 24

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 3 Further Illustration of Theorem 2 Using (4), find the inverse of Section 7. 8 p 25

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 3 (continued) Further Illustration of Theorem 2 Solution. We obtain det A = − 1(− 7) − 1 · 13 + 2 · 8 = 10, and in (4), Section 7. 8 p 26

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination EXAMPLE 3 (continued) Further Illustration of Theorem 2 Solution. (continued) so that by (4), in agreement with Example 1, Section 7. 8 p 27

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Products can be inverted by taking the inverse of each factor and multiplying these inverses in reverse order, (AC)− 1 = C− 1 A− 1. (7) Hence for more than two factors, (8) (AC … PQ)− 1 = Q− 1 P− 1 … C− 1 A− 1. Section 7. 8 p 28

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Unusual Properties of Matrix Multiplication. Cancellation Laws [1] Matrix multiplication is not commutative, that is, in general we have AB ≠ BA. [2] AB = 0 does not generally imply A = 0 or B = 0 (or BA = 0); for example, [3] AC = AD does not generally imply C = D (even when A ≠ 0). Section 7. 8 p 29

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination THEOREM 3 Cancellation Laws Let A, B, C be n × n matrices. Then: (a) If rank A = n and AB = AC, then B = C. (b) If rank A = n, then AB = 0 implies B = 0. Hence if AB = 0, but A ≠ 0 as well as B ≠ 0, then rank A < n and rank B < n. (c) If A is singular, so are BA and AB. Section 7. 8 p 30

7. 8 Inverse of a Matrix. Gauss–Jordan Elimination Determinants of Matrix Products THEOREM 4 Determinant of a Product of Matrices For any n × n matrices A and B, (10) Section 7. 8 p 31 det (AB) = det (BA) = det A det B.

7. 9 Vector Spaces, Inner Product Spaces, Linear Transformations Optional Linear Transformations Let X and Y be any vector spaces. To each vector x in X we assign a unique vector y in Y. Then we say that a mapping (or transformation or operator) of X into Y is given. Such a mapping is denoted by a capital letter, say F. The vector y in Y assigned to a vector x in X is called the image of x under F and is denoted by F(x) [or Fx, without parentheses]. Section 7. 9 p 32

7. 9 Vector Spaces, Inner Product Spaces, Linear Transformations Optional Linear Transformations (continued) F is called a linear mapping or linear transformation if, for all vectors v and x in X and scalars c, (10) Section 7. 9 p 33

7. 9 Vector Spaces, Inner Product Spaces, Linear Transformations Optional Linear Transformations (continued) Linear Transformation of Space Rn into Space Rm From now on we let X = Rn and Y = Rm. Then any real m × n matrix A = [ajk] gives a transformation of Rn into Rm, (11) y = Ax. Since A(u + x) = Au + Ax and A(cx) = c. Ax, this transformation is linear. Section 7. 9 p 34

7. 9 Vector Spaces, Inner Product Spaces, Linear Transformations Optional Linear Transformations (continued) If A in (11) is square, n × n, then (11) maps Rn into Rn. If this A is nonsingular, so that A− 1 exists (see Sec. 7. 8), then multiplication of (11) by A− 1 from the left and use of A− 1 A = I gives the inverse transformation (14) x = A− 1 y. It maps every y = y 0 onto that x, which by (11) is mapped onto y 0. The inverse of a linear transformation is itself linear, because it is given by a matrix, as (14) shows. Section 7. 9 p 35

7. 9 Vector Spaces, Inner Product Spaces, Linear Transformations Optional Composition of Linear Transformations Let X, Y, W be general vector spaces. As before, let F be a linear transformation from X to Y. Let G be a linear transformation from W to X. Then we denote, by H, the composition of F and G, that is, H = F ◦ G = F(G), which means we take transformation G and then apply transformation F to it (in that order!, i. e. , you go from left to right). Section 7. 9 p 36

7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems SUMMARY OF CHAPTER Section 7. Summary p 37

SUMMARY OF CHAPTER 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems An m × n matrix A = [ajk] is a rectangular array of numbers or functions (“entries, ” “elements”) arranged in m horizontal rows and n vertical columns. If m = n, the matrix is called square. A 1 × n matrix is called a row vector and an m × 1 matrix a column vector (Sec. 7. 1). The sum A + B of matrices of the same size (i. e. , both m × n) is obtained by adding corresponding entries. The product of A by a scalar c is obtained by multiplying each ajk by c (Sec. 7. 1). Section 7. Summary p 38

SUMMARY OF CHAPTER 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems (continued 1) The product C = AB of an m × n matrix A by an r × p matrix B = [bjk] is defined only when r = n, and is the m × p matrix C = [cjk] with entries (1) cjk = aj 1 b 1 k + aj 2 b 2 k + … + ajnbnk (row j of A times column k of B). This multiplication is motivated by the composition of linear transformations (Secs. 7. 2, 7. 9). It is associative, but is not commutative: if AB is defined, BA may not be defined, but even if BA is defined, AB ≠ BA in general. Also AB = 0 may not imply A = 0 or BA = 0 (Secs. 7. 2, 7. 8). Section 7. Summary p 39

SUMMARY OF CHAPTER (continued 2) Illustrations: Section 7. Summary p 40 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems

SUMMARY OF CHAPTER (continued 3) 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems The transpose AT of a matrix A = [ajk] is AT = [ajk]; rows become columns and conversely (Sec. 7. 2). Here, A need not be square. If it is and A = AT, then A is called symmetric; if A = −AT, it is called skew-symmetric. For a product, (AB)T = BTAT (Sec. 7. 2). A main application of matrices concerns linear systems of equations (2) Ax = b (Sec. 7. 3) (m equations in n unknowns x 1, … , xn; A and b given). Section 7. Summary p 41

SUMMARY OF CHAPTER (continued 4) 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems The most important method of solution is the Gauss elimination (Sec. 7. 3), which reduces the system to “triangular” form by elementary row operations, which leave the set of solutions unchanged. (Numeric aspects and variants, such as Doolittle’s and Cholesky’s methods, are discussed in Secs. 20. 1 and 20. 2. ) Cramer’s rule (Secs. 7. 6, 7. 7) represents the unknowns in a system (2) of n equations in n unknowns as quotients of determinants; for numeric work it is impractical. Determinants (Sec. 7. 7) have decreased in importance, but will retain their place in eigenvalue problems, elementary geometry, etc. Section 7. Summary p 42

SUMMARY OF CHAPTER (continued 5) 7 Linear Algebra: Matrices, Vectors, Determinants. Linear Systems The inverse A− 1 of a square matrix satisfies A A− 1 = A− 1 A = I. It exists if and only if det A ≠ 0. It can be computed by the Gauss–Jordan elimination (Sec. 7. 8). The rank r of a matrix A is the maximum number of linearly independent rows or columns of A or, equivalently, the number of rows of the largest square submatrix of A with nonzero determinant (Secs. 7. 4, 7. 7). The system (2) has solutions if and only if rank A = rank [A b], where [A b] is the augmented matrix (Fundamental Theorem, Sec. 7. 5). Section 7. Summary p 43

SUMMARY OF CHAPTER (continued 6) Linear Algebra: Matrices, Vectors, Determinants. Linear Systems The homogeneous system (3) Ax = 0 has solutions x ≠ 0 (“nontrivial solutions”) if and only if rank A < n, in the case m = n equivalently if and only if det A = 0 (Secs. 7. 6, 7. 7). Vector spaces, inner product spaces, and linear transformations are discussed in Sec. 7. 9. See also Sec. 7. 4. Section 7. Summary p 44 7
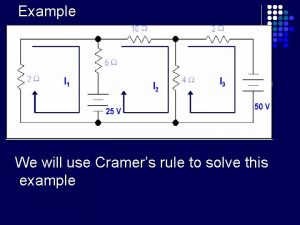
 Cramers rule
Cramers rule Cramer's rule 3 by 3 matrix
Cramer's rule 3 by 3 matrix Cramers rule 3x3
Cramers rule 3x3 Cramers v interpretation
Cramers v interpretation Phi(n) formula
Phi(n) formula Cramers v
Cramers v Cramers v
Cramers v Special angles triangles
Special angles triangles When to use sine rule and cosine rule
When to use sine rule and cosine rule Sohcahtoa rule
Sohcahtoa rule Junction rule and loop rule
Junction rule and loop rule Sum rule and product rule
Sum rule and product rule Dillon rule
Dillon rule Kirchhoff's loop rule example
Kirchhoff's loop rule example Horizontal line vertical line
Horizontal line vertical line Astigmatism examples
Astigmatism examples Astigmatisml
Astigmatisml Product rule vs chain rule
Product rule vs chain rule General power rule vs power rule
General power rule vs power rule Sine and cosine rules
Sine and cosine rules Chain rule power rule
Chain rule power rule Tukey's rule vs empirical rule
Tukey's rule vs empirical rule What are the determinants of market structure
What are the determinants of market structure Chapter 6 section 1 combining supply and demand answers
Chapter 6 section 1 combining supply and demand answers Non price determinants of supply
Non price determinants of supply Non price determinants of supply
Non price determinants of supply Non price determinants of supply
Non price determinants of supply Non price determinants of supply
Non price determinants of supply What are the determinants of market structure
What are the determinants of market structure What are the 6 main social determinants of health?
What are the 6 main social determinants of health? Social determinants of personality
Social determinants of personality Les déterminants synthèse
Les déterminants synthèse Pes determinants
Pes determinants Sr model of human behaviour
Sr model of human behaviour Augmented matrix
Augmented matrix Determinants of staffing choices
Determinants of staffing choices What are the 5 determinants of price elasticity of demand
What are the 5 determinants of price elasticity of demand Define elasticity of demand
Define elasticity of demand Elasticity and its application in economics
Elasticity and its application in economics Cytoplasmic determinants
Cytoplasmic determinants Determinants of gait
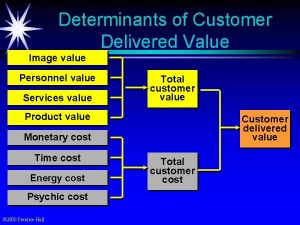
Determinants of gait Personnel value
Personnel value What are the determinants of market structure
What are the determinants of market structure Functional cost
Functional cost 4 types of readiness to learn
4 types of readiness to learn