7 7 Base e and Natural Logarithms Natural

7. 7 – Base e and Natural Logarithms

Natural Base (base e) • f(x) = ex and f(x) = e-x • If graphed, they follow rules of exponential growth or decay.

Remember… • Logbx and bx are inverses of each other • Since we are working with ex in this section, it’s inverse will be logex. – This is the natural logarithm – Usually written as ln x

Example 1: A. Write an equivalent logarithmic equation for ex = 23. B. What is e 4 = x in logarithmic form?

Example 2: A. Write ln 25 = x in exponential form. B. Write ln 47 = x in exponential form.

Example 3: Condense A. Write 4 ln 3 + ln 6 as a single logarithm. B. Write 2 ln 3 + ln 4 + ln y as a single logarithm.

Example 4 a: Solve Base e Equations Solve 3 e– 2 x + 4 = 10. Round to the nearest ten-thousandth.

Example 4 b: Solve Base e Equations Solve the exponential equation. Round to the nearest ten-thousandth.

Example 5 a: Solve Natural Log Equations Solve the logarithmic equation. Round to the nearest ten-thousandth. 2 ln 5 x = 6

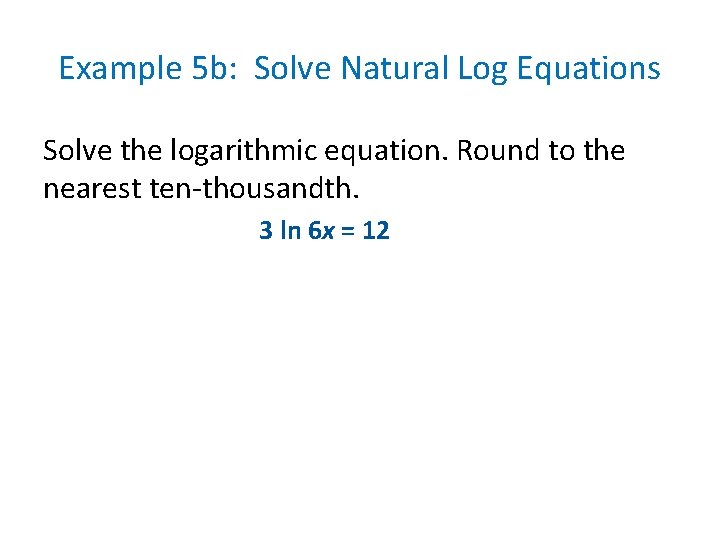
Example 5 b: Solve Natural Log Equations Solve the logarithmic equation. Round to the nearest ten-thousandth. 3 ln 6 x = 12

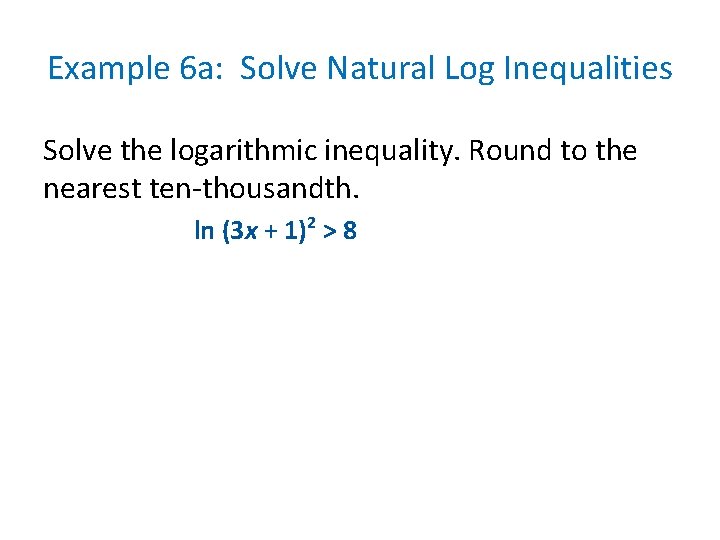
Example 6 a: Solve Natural Log Inequalities Solve the logarithmic inequality. Round to the nearest ten-thousandth. ln (3 x + 1)2 > 8

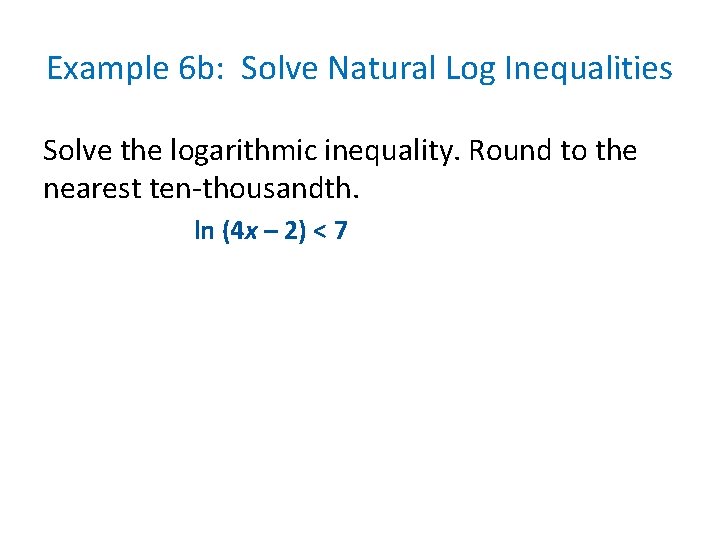
Example 6 b: Solve Natural Log Inequalities Solve the logarithmic inequality. Round to the nearest ten-thousandth. ln (4 x – 2) < 7

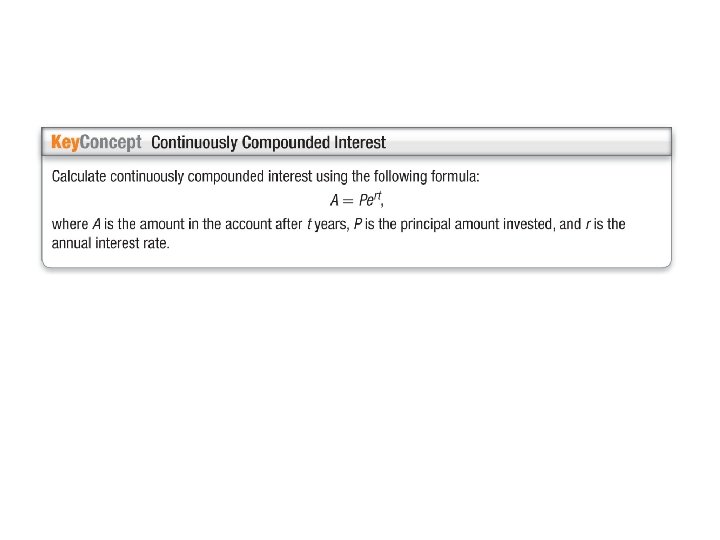
Example 7: A. Suppose you deposit $700 into an account paying 3% annual interest, compounded continuously. What is the balance after 8 years?

Example 7: B. Suppose you deposit $700 into an account paying 2. 4% annual interest, compounded continuously. How long will it take for the balance in your account to reach at least $1200?

Example 7: C. Suppose you deposit money into an account paying 3% annual interest, compounded continuously. How much would have to be deposited in order to reach a balance of $1950 after 10 years?