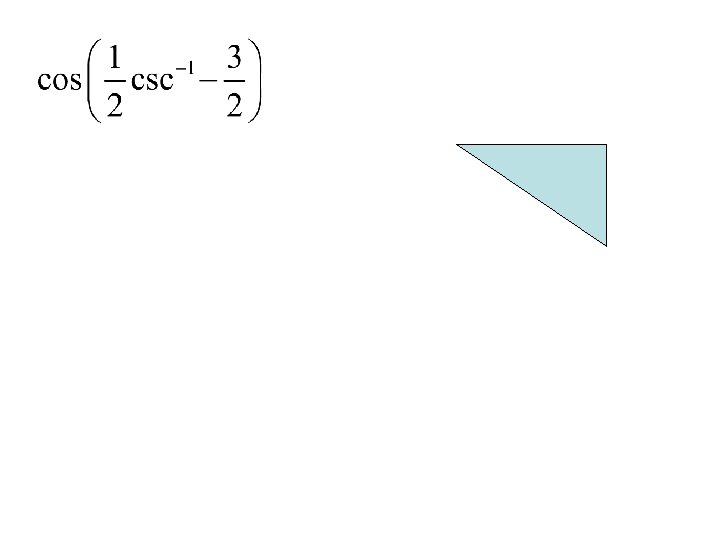7 6 Solving Trigonometric Equations Finding what x

It is just like solving regular equations, but once you get solutions, you have

What are the rules? 1. “x” means give the answer in _____; “Θ” means

Is that it? Well, yes, except for one footnote. Never divide both sides by

7 -6 Solving Trigonometric Equations Day 2

Lets go back to the solutions from yesterday and turn them into general solutions.

6 -5 Inverse Trig An Inverse Function What was that again?

Lets remember: What is an inverse function? What is the notation? ______________ In a

f(x) = sin x f(x) = sin-1 x What is the problem here? _______________

How do we take care of that? Therefore, there are limits on the answers

Each function has a limited Range For sin-1 x, csc-1 x, tan-1 x ______________

REMEMBER With inverse trig you give only _______________________ An answer in quadrant 4 such

A Hint To give yourself something to remember, use the phrase “What angle has

We will now combine Inverse Trig with: • Addition and Subtraction Formulas • Double

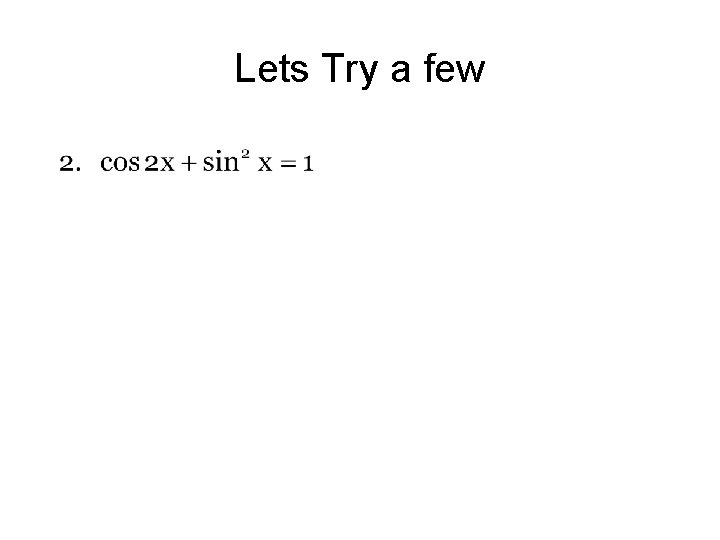
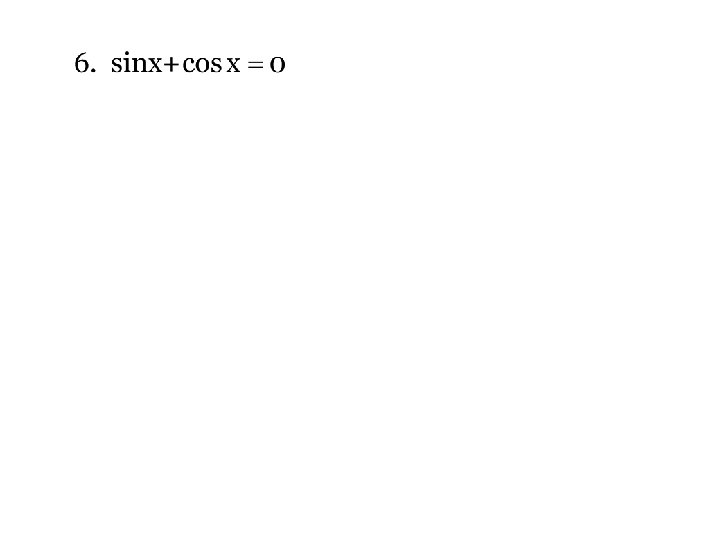
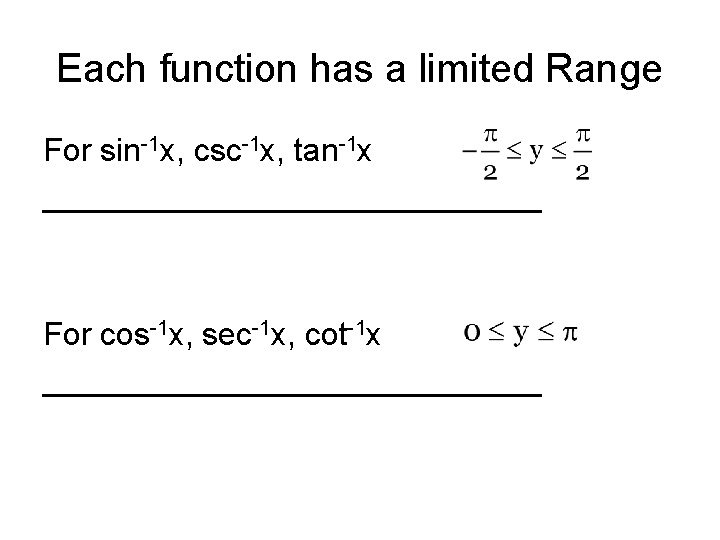
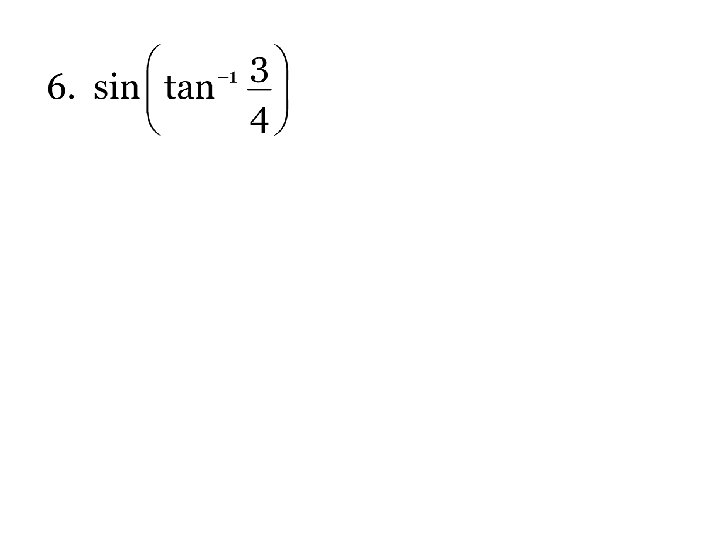
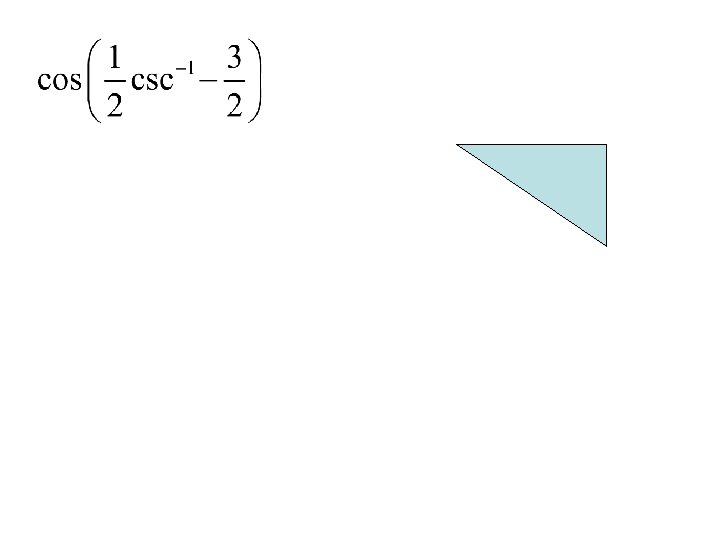
Slides: 30

Download presentation

7 -6 Solving Trigonometric Equations Finding what x equals

It is just like solving regular equations, but once you get solutions, you have to find corresponding angle measure. Lets try a problem then see the rules.

What are the rules? 1. “x” means give the answer in _____; “Θ” means give the answer in ______. 2. “Solve for 0 ≤ x < 2π” means give all the answers on one pass around the unit circle. 3. “General solution” means ________________________ 4. Guess what: Work on both sides of the equation using all the rules of algebra. That is a) _______ or b) ______

Is that it? Well, yes, except for one footnote. Never divide both sides by the same trig function to get rid of it. For example, It will eliminate answers.

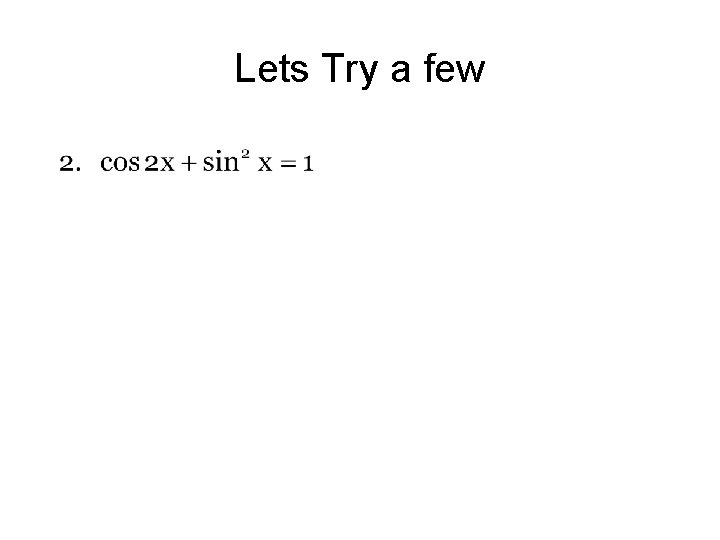
Lets Try a few

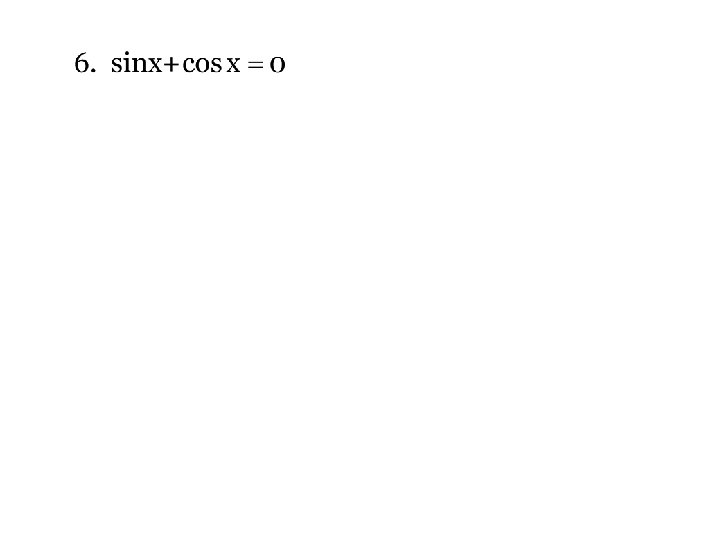
7 -6 Solving Trigonometric Equations Day 2

Lets go back to the solutions from yesterday and turn them into general solutions. • General Solutions will help you find every single solution no matter how many times around the circle • All we do is add after the answers for one time around the circle. • Or for tangent answers because ___________________________________

General Solution

6 -5 Inverse Trig An Inverse Function What was that again?

Lets remember: What is an inverse function? What is the notation? ______________ In a way, you have been practicing the inverse trig process. In section 7 -6, you had the trig value and found the angle.

f(x) = sin x f(x) = sin-1 x What is the problem here? _______________

How do we take care of that? Therefore, there are limits on the answers that you can get. Use your calculator to find cos-1(-. 5) _____________________________

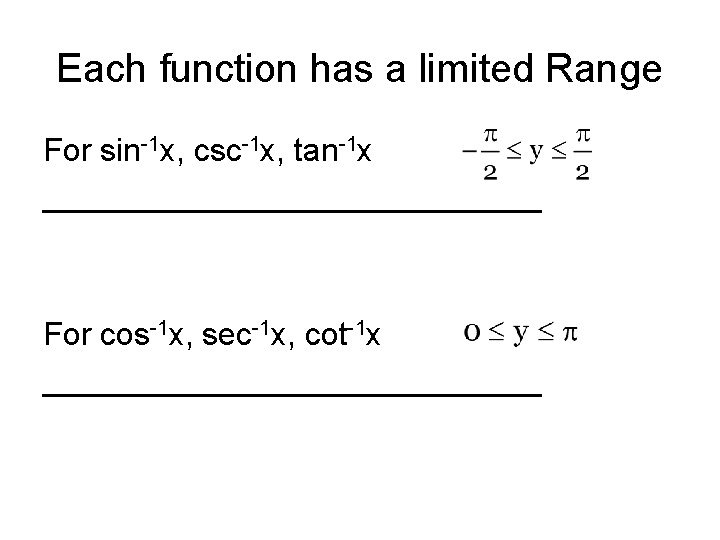
Each function has a limited Range For sin-1 x, csc-1 x, tan-1 x ______________ For cos-1 x, sec-1 x, cot-1 x ______________

REMEMBER With inverse trig you give only _______________________ An answer in quadrant 4 such as 300 must be given as -60. BE Careful!!

A Hint To give yourself something to remember, use the phrase “What angle has a” for the symbol -1. SO, lets try some problems.

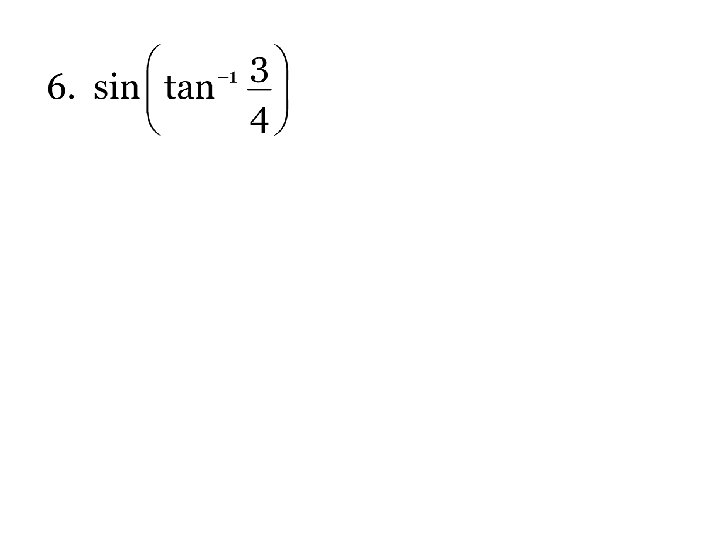
Inverse Rule

6 -5 Day 2 Inverse Trig Continued

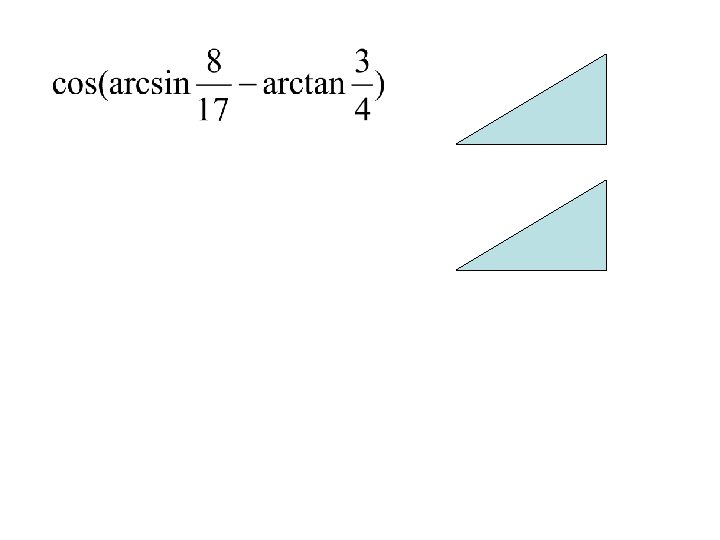
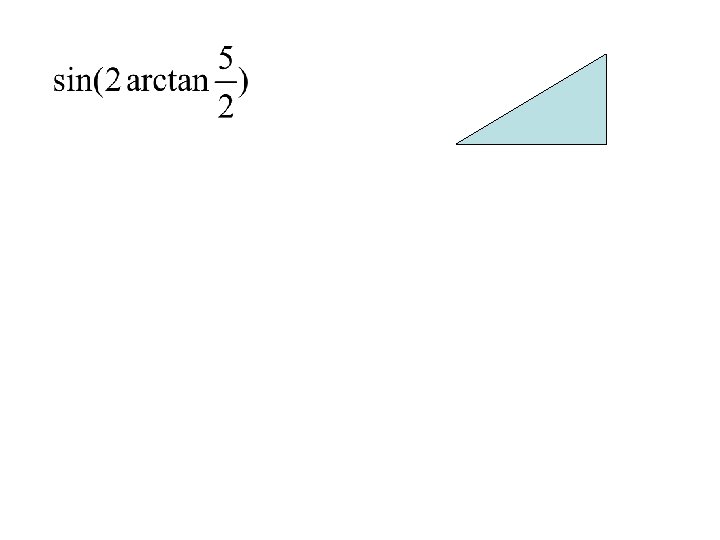
We will now combine Inverse Trig with: • Addition and Subtraction Formulas • Double Angle Formulas • Half Angle Formulas

Example A B