7 5 InclusionExclusion The Principle of InclusionExclusion Example

7. 5 Inclusion-Exclusion The Principle of Inclusion-Exclusion • Example 1: In a discrete mathematics class every student is a major in computer science or mathematics, or both. • The number of students having computer science as a major (possibly along with mathematics) is 25; • the number of students having mathematics as a major (possibly along with computer science) is 13; • and the number of students majoring in both computer science and mathematics is 8. • How many students are in this class? FIGURE 1 The Set of Students in a Discrete Mathematics Class. 1

The Principle of Inclusion-Exclusion • Example 2: How many positive integers not exceeding 1000 are divisible by 7 or 11? FIGURE 2 The Set of Positive Integers Not Exceeding 1000 Divisible by Either 7 or 11. • HW: Example 3, (p. 501) 2

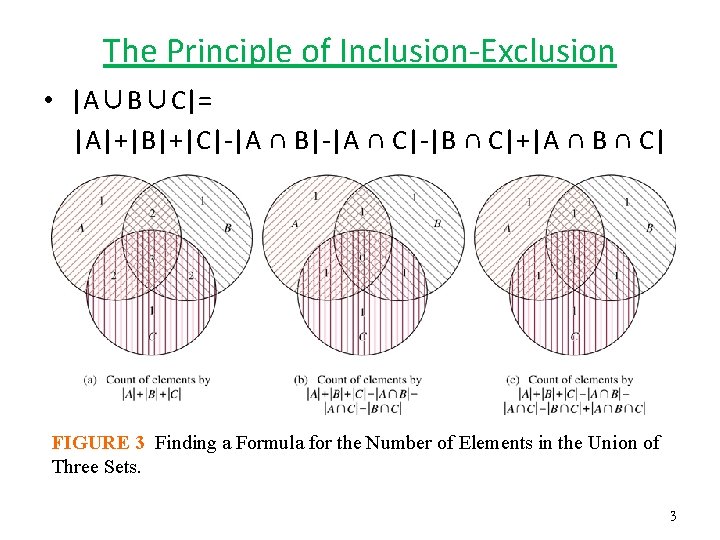
The Principle of Inclusion-Exclusion • |A∪B∪C|= |A|+|B|+|C|-|A ∩ B|-|A ∩ C|-|B ∩ C|+|A ∩ B ∩ C| FIGURE 3 Finding a Formula for the Number of Elements in the Union of Three Sets. 3

The Principle of Inclusion-Exclusion • Example 4: A total of 1232 • how many students have taken a course in all three course in Spanish, languages? • 879 have taken a course in French, and • 114 have taken a course in Russian. • 103 have taken courses in both Spanish and French, • 23 have taken courses in both Spanish and Russian , and • 14 have taken course in both French and Russian. • If 2092 students have taken at least one of Spanish, FIGURE 4 The Set of Students Who Have Taken French, and Russian. Courses in Spanish, French, and Russian. 4

The Principle of Inclusion-Exclusion • Theorem 1: The Principle of Inclusion-Exclusion • Let A 1, A 2, . . . , An be finite sets. Then • Example 5: Give a formula for the number of elements in the union of four sets. 5