7 3 Solving Systems Using Addition and Subtraction

7. 3 Solving Systems Using Addition and Subtraction

EXAMPLE 1 Use addition to eliminate a variable Solve the linear system: 2 x + 3 y = 11 – 2 x + 5 y = 13 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 Add the equations to eliminate one variable. Solve for y. 2 x + 3 y = 11 – 2 x +5 y = 13 8 y = 24 y=3 Substitute 3 for y in either equation and Solve for x.

EXAMPLE 1 Use addition to eliminate a variable 2 x + 3 y = 11 2 x + 3(3) = 11 x=1 ANSWER The solution is (1, 3). Write Equation 1 Substitute 3 for y. Solve for x.

EXAMPLE 2 Use subtraction to eliminate a variable Solve the linear system: 4 x + 3 y = 2 5 x + 3 y = – 2 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 Subtract the equations to eliminate one variable. Solve for x. 4 x + 3 y = 2 5 x + 3 y = – 2 –x = 4 STEP 3 Substitute 4 for x in either equation and solve for y.

EXAMPLE 2 Use subtraction to eliminate a variable 4 x + 3 y = 2 Write Equation 1. Substitute – 4 for x. 4(– 4) + 3 y = 2 y=2 Solve for y. ANSWER The solution is (– 4, 6).

EXAMPLE 3 Arrange like terms Solve the linear system: 8 x – 4 y = – 4 4 y = 3 x + 14 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 STEP 4 Rewrite Equation 2 so that the like terms are arranged in columns. 8 x – 4 y = – 4 4 y = 3 x + 14 3 x + 4 y = 14 5 x = 10 Add the equations. Solve for x. x=2 Substitute 2 for x in either equation and solve for y.

EXAMPLE 3 Arrange like terms 4 y = 3 x + 14 4 y = 3(2) + 14 y=5 Write Equation 2. Substitute 2 for x. Solve for y. ANSWER The solution is (2, 5).

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 1. 4 x – 3 y = 5 – 2 x + 3 y = – 7 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 Add the equations to eliminate one variable. Solve for x. 4 x – 3 y = 5 – 2 x +3 y = – 7 2 x = – 2 x=– 1 Substitute – 1 for y in either equation and Solve for x.

GUIDED PRACTICE for Example 1, 2 and 3 4 x – 3 y = 5 2(– 1) – 3 y = 5 y=– 3 Write Equation 1. ANSWER The solution is (– 1, – 3). Substitute – 1 for x. Solve for x.

GUIDED PRACTICE CHECK for Example 1, 2 and 3 Substitute 1 for x and 3 for y in each of the. original equation 4 x – 3 y = 5 4(– 1) – 3(– 3) =? 5 5=5 – 2 x + 3 y = – 7 ? – 7 – 2(– 1) + 5(– 3) = – 7=– 7

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 2. – 5 x – 6 y = 8 5 x + 2 y = 4 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 Add the equations to eliminate one variable. Solve for y. – 5 x – 6 y = 8 5 x + 2 y = 4 – 4 y = 12 y=– 3 Substitute – 3 for y in either equation and solve for y.

GUIDED PRACTICE for Example 1, 2 and 3 Write Equation 1. – 5 x – 6 y = 8 Substitute – 3 for y. – 5 x – 6(– 3) = 8 Solve for x. x=2 ANSWER The solution is (2, 5).

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 3. 6 x – 4 y = 14 – 3 x + 4 y = 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 Add the equations to eliminate one variable. Solve for x. 6 x – 4 y = 14 – 3 x + 4 y = 1 3 x = 15 x = 5 Substitute 5 for x in either equation and solve for y.

GUIDED PRACTICE for Example 1, 2 and 3 Write Equation 1. 6 x – 4 y = 14 Substitute 5 for x. 6(5) – 4 y = 14 Solve for y. y=4 ANSWER The solution is (5, 4).

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 4. 7 x – 2 y = 5 7 x – 3 y = 4 Equation 1 Equation 2 SOLUTION STEP 1 STEP 2 STEP 3 Subtract the equations to eliminate one variable. Solve for y. 7 x – 2 y = 5 7 x – 3 y = 4 y= 1 Substitute 1 for y in either and solve for x.

GUIDED PRACTICE for Example 1, 2 and 3 Write Equation 1. 7 x – 2 y = 5 Substitute 1 for y. 7 x – 2(1) = 5 Solve for x. x=1 ANSWER The solution is (1, 1).

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 5. 3 x + 4 y = – 6 2 y = 3 x + 6 Equation 1 Equation 2 SOLUTION STEP 1 Rewrite Equation 2 so that the like terms are arranged in columns. 3 x + 4 y = – 6 2 y = 3 x + 6 3 x – 2 y = – 6 STEP 2 STEP 3 STEP 4 6 y = 0 Subtract the equations. Solve for y. y=0 Substitute 0 for y in either equation and solve for x.

GUIDED PRACTICE 2 y = 3 x + 6 2(0) = 3 x + 6 x=– 2 for Example 1, 2 and 3 Write Equation 2. Substitute 0 for y. Solve for x. ANSWER The solution is (– 2, 0).

GUIDED PRACTICE for Example 1, 2 and 3 Solve the linear system: 6. 2 x + 5 y = 12 5 y = 4 x + 6 Equation 1 Equation 2 SOLUTION STEP 1 Rewrite Equation 2 so that the like terms are arranged in columns. 2 x + 5 y = 12 5 y = 4 x + 6 – 4 x + 5 y = 6 STEP 2 STEP 3 STEP 4 Subtract the equations. 6 x = 6 Solve for x. x=1 Substitute 1 for x in either equation and solve for y.

GUIDED PRACTICE 2 x + 5 y = 12 2(1) + 5 y = 6 x= 2 for Example 1, 2 and 3 Write Equation 2. Substitute 1 for x. Solve for y. ANSWER The solution is (1, 2).

EXAMPLE 4 Write and solve a linear system KAYAKING During a kayaking trip, a kayaker travels 12 miles upstream (against the current) and 12 miles downstream (with the current), as shown. The speed of the current remained constant during the trip. Find the average speed of the kayak in still water and the speed of the current.

EXAMPLE 4 Write and solve a linear system STEP 1 Write a system of equations. First find the speed of the kayak going upstream and the speed of the kayak going downstream. Upstream: d = rt 12 = r 3 4=r Downstream: d = rt 12 = r 2 6=r

EXAMPLE 4 Write and solve a linear system Use the speeds to write a linear system. Let x be the average speed of the kayak in still water, and let y be the speed of the current. Equation 1: Going upstream x – y = 4

EXAMPLE 4 Write and solve a linear system Equation 2: Going downstream x + y = 6

EXAMPLE 4 Write and solve a linear system STEP 2 Solve the system of equations. x – y= 4 Write Equation 1. x+y=6 Write Equation 2. 2 x = 10 x=5 Add equations. Solve for x. Substitute 5 for x in Equation 2 and solve for y.

EXAMPLE 4 Write and solve a linear system 5+y=6 y=1 Substitute 5 for x in Equation 2. Subtract 5 from each side.

GUIDED PRACTICE for Example 4 7. WHAT IF? In Example 4, suppose it takes the kayaker 5 hours to travel 10 miles upstream and 2 hours to travel 10 miles downstream. The speed of the current remains constant during the trip. Find the average speed of the kayak in still water and the speed of the current. SOLUTION STEP 1 Write a system of equations. First find the speed of the kayakar going downstream.

GUIDED PRACTICE Upstream: d = rt 10 = r 5 2=r for Example 4 Downstream: d = rt 10 = r 2 5=r Use the speeds to write a linear system. Let x be the average speed of the kayakar in still water, and let y be the speed of the current.

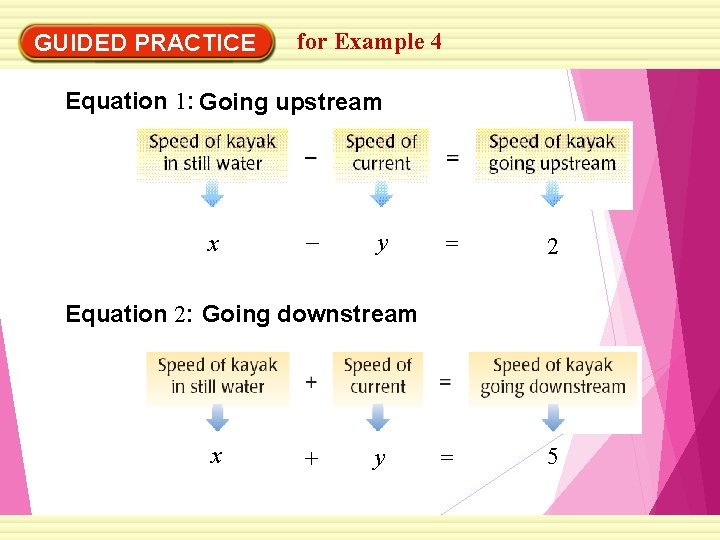
GUIDED PRACTICE for Example 4 Equation 1: Going upstream x – y = 2 = 5 Equation 2: Going downstream x + y

GUIDED PRACTICE for Example 4 STEP 2 Solve the system of equations. x – y= 2 Equation 1. x+y=5 Equation 2. 2 x =7 x = 3. 5 Add equations. Solve for x. Substitute 3. 5 for x in Equation 2 and solve for y.

GUIDED PRACTICE 3. 5 + y = 6 y = 1. 5 for Example 4 Substitute 3. 5 for x in Equation 2. Subtract 3. 5 from each side. ANSWER The average speed of the kayakar in still water is 3. 5 miles per hour, and the speed of the current is 1. 5 mile per hour.