7 3 Proving Triangles Similar Name the postulate

7. 3 Proving Triangles Similar Name the postulate or theorem you can use to prove the triangles congruent. 1. 2. 3. Objectives: To use the AA ∼ Postulate and the SAS ∼ and SSS ∼ Theorems To use similarity to find indirect measurements Click for next slide

Essential Understanding You can show that two triangles are similar when you know the relationships between only two or three pairs of corresponding parts. Click for next slide

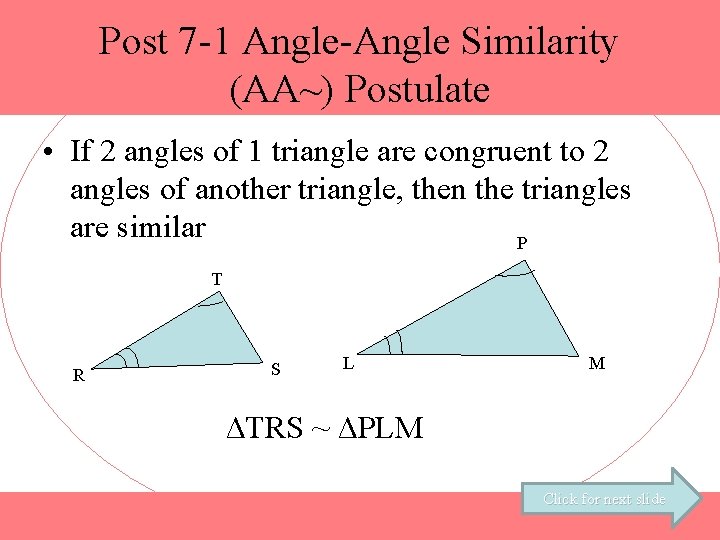
Post 7 -1 Angle-Angle Similarity (AA~) Postulate • If 2 angles of 1 triangle are congruent to 2 angles of another triangle, then the triangles are similar P T R S L M ΔTRS ~ ΔPLM Click for next slide

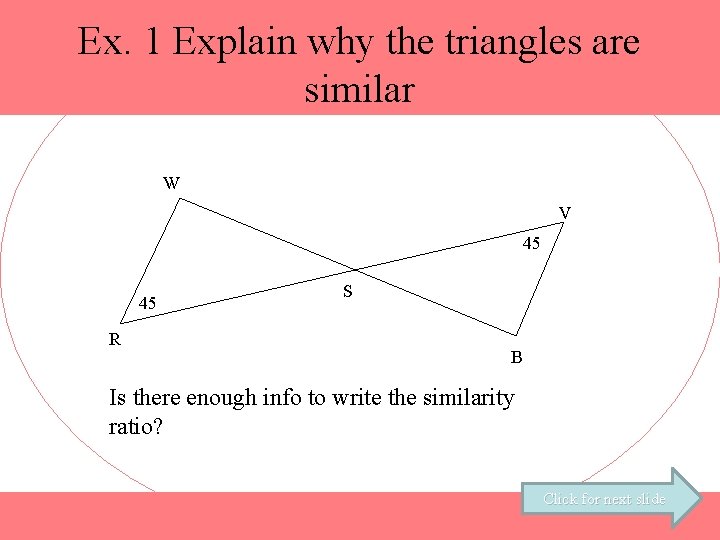
Ex. 1 Explain why the triangles are similar W V 45 45 R S B Is there enough info to write the similarity ratio? Click for next slide

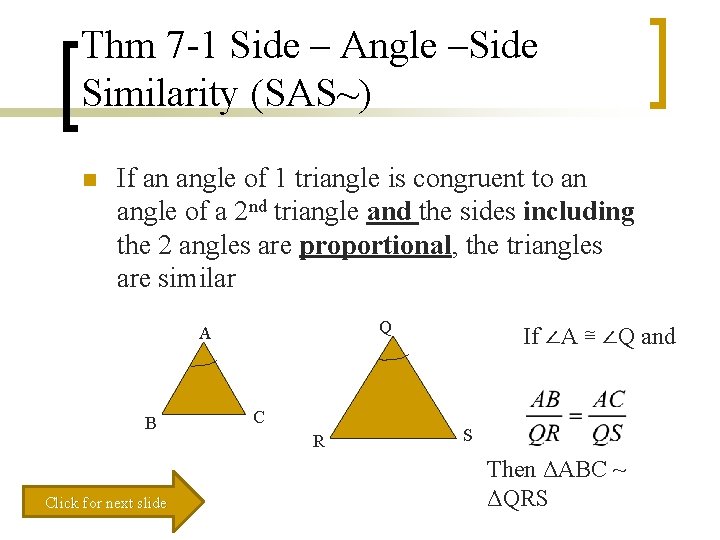
Thm 7 -1 Side – Angle –Side Similarity (SAS~) n If an angle of 1 triangle is congruent to an angle of a 2 nd triangle and the sides including the 2 angles are proportional, the triangles are similar Q A B Click for next slide C R If ∠A ≅ ∠Q and S Then ΔABC ~ ΔQRS

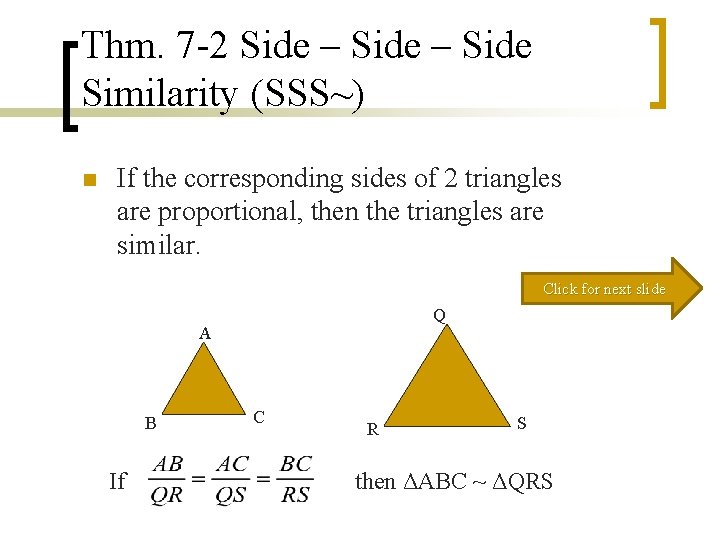
Thm. 7 -2 Side – Side Similarity (SSS~) n If the corresponding sides of 2 triangles are proportional, then the triangles are similar. Click for next slide Q A B If C R S then ΔABC ~ ΔQRS

Ex. 2 Explain why the following triangles are similar M a) b) Z P K 6 A 58 X 58 B Q 3 8 R X 4 Y Given: MX ⊥ AB Click for next slide

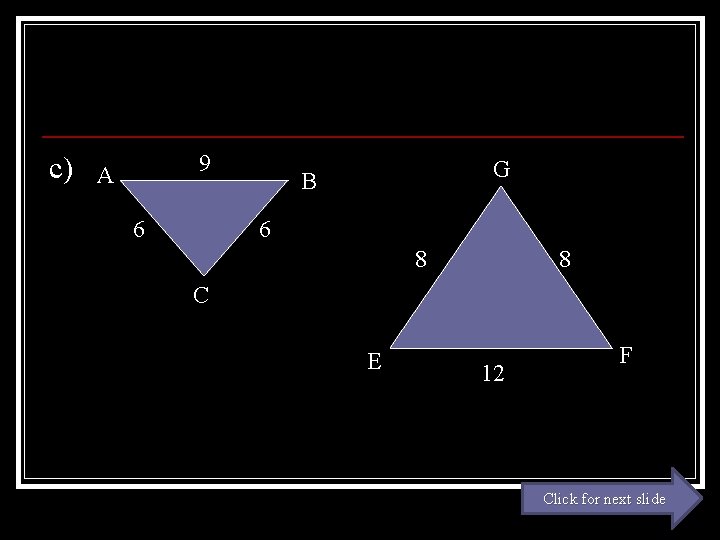
c) 9 A 6 G B 6 8 8 C E 12 F Click for next slide

• The lengths of the sides of similar triangles can be found by using Similar Theorems. Click for next slide

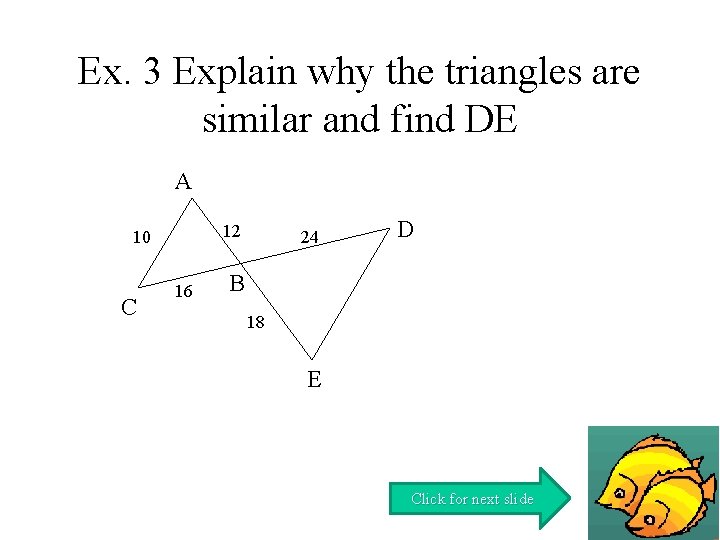
Ex. 3 Explain why the triangles are similar and find DE A 12 10 C 16 24 D B 18 E Click for next slide

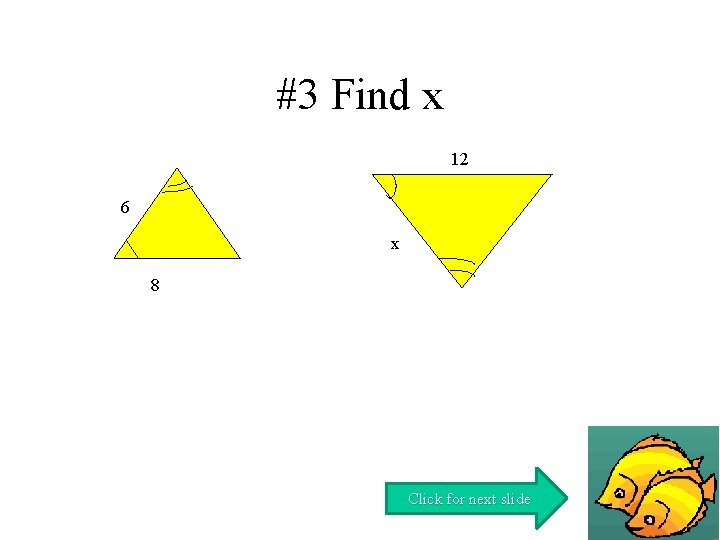
#3 Find x 12 6 x 8 Click for next slide

Indirect measurements • Measurement that would be hard to actually measure. • Can use similar triangles to find these measurements. Click for next slide

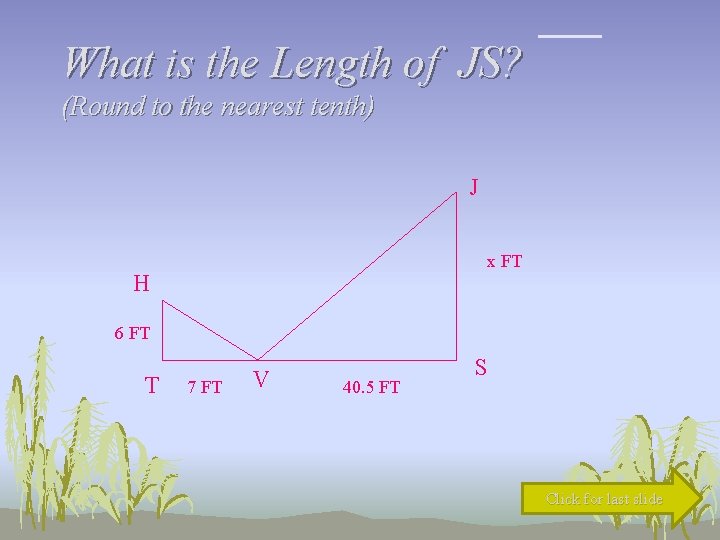
What is the Length of JS? (Round to the nearest tenth) J x FT H 6 FT T 7 FT V 40. 5 FT S Click for last slide

Classwork 7. 3 Review Worksheet LESSON OVER