7 2 Notes Similar Polygons Todays Objectives 1

7. 2 Notes Similar Polygons Today’s Objectives: 1. Students will be able to use proportions to identify similar polygons. 2. Students will be able to solve problems using the properties of similar polygons.

Similar Polygons - have the same shape but not necessarily the same size. - Two polygons are similar if and only if the angles are congruent and the side lengths are proportional. Similarity - Just like congruency statements, but with the Statements similar symbol.

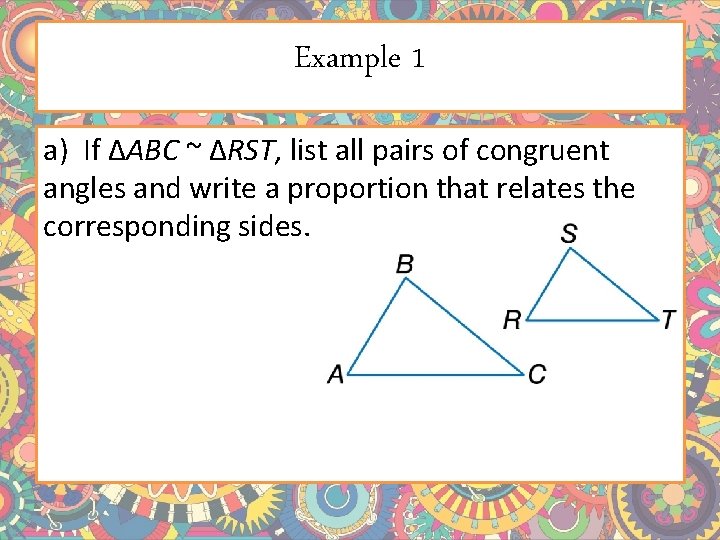
Example 1 a) If ΔABC ~ ΔRST, list all pairs of congruent angles and write a proportion that relates the corresponding sides.
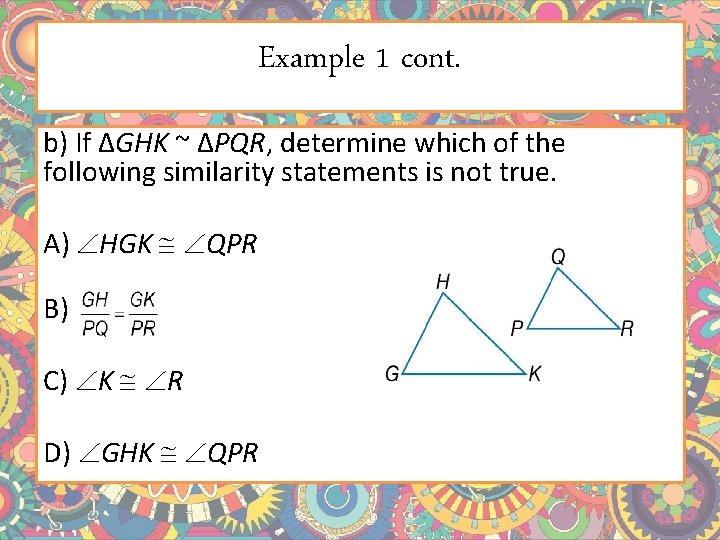
Example 1 cont. b) If ΔGHK ~ ΔPQR, determine which of the following similarity statements is not true. A) HGK QPR B) C) K R D) GHK QPR

Example 2: Determine whether each pair of figures is similar. Justify your answer.

Vocab! Scale Factor

Does it matter which polygon you start first when finding the scale factor? • Always start with first polygon mentioned!

Example 3: This is a miniature replica of a 1923 Checker Cab. The length of the model is 6. 5 inches long. If the length of the car is 13 feet, what is the scale factor of the model compared to the car?

Example 4: The height of the Alamo is 33 feet 6 inches. The height of a model is 3 feet. What is the scale factor of the model compared to the original?

Example 3 a) The two polygons are similar. Find the values of x and y.

You Try! b) The two polygons are similar. Solve for a and b.

Vocab Perimeters of Similar Polygons - If 2 polygons are similar, then their perimeters are proportional to the scale factor between them.
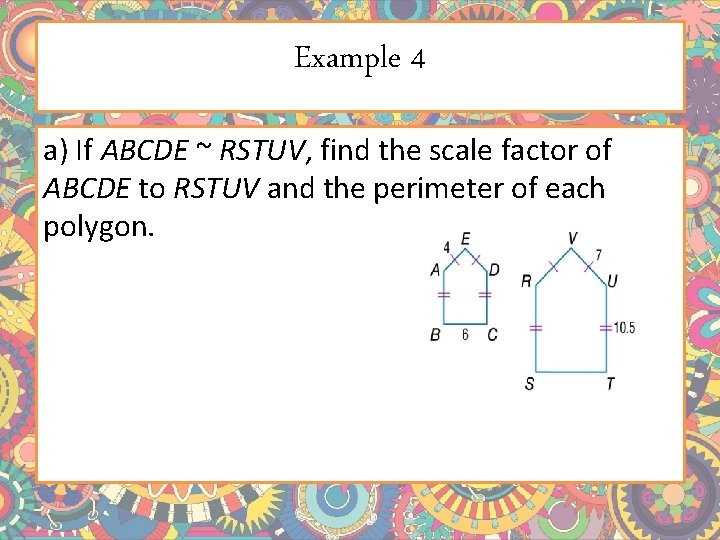
Example 4 a) If ABCDE ~ RSTUV, find the scale factor of ABCDE to RSTUV and the perimeter of each polygon.
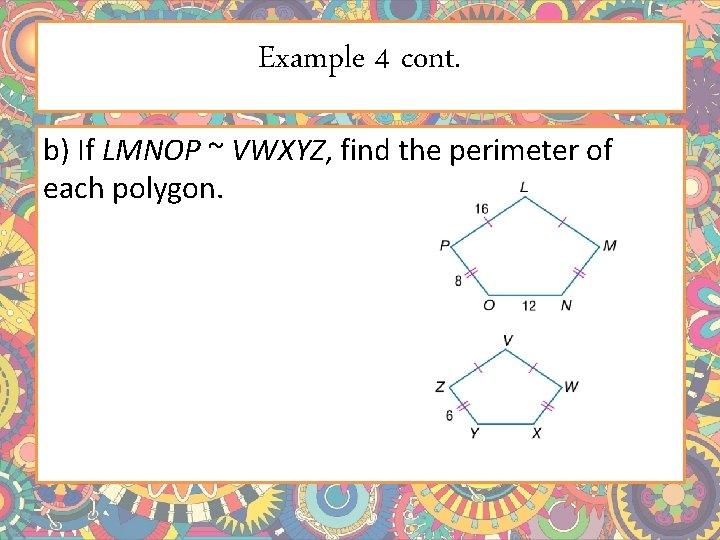
Example 4 cont. b) If LMNOP ~ VWXYZ, find the perimeter of each polygon.

You Try! •

Summary •

Summary •

Homework: pg. 473, #8, 12, 15, 18, 20, 23, 24, 28, 36
- Slides: 19