7 1 Geometric Mean Objectives Find the geometric

7. 1 Geometric Mean

Objectives � Find the geometric mean between two numbers � Solve problems involving relationships between parts of right triangles and the altitude to its hypotenuse

Geometric Mean � The geometric mean between two numbers is the positive square root of their products. � In other words, given two positive numbers such as a and b, the geometric mean is the positive number x such that a: x=x: b We can also write this as fractions, a/x=x/b or as cross products, x 2 = ab.

Example 1 a: Find the geometric mean between 2 and 50. Let x represent the geometric mean. Definition of geometric mean Cross products Take the positive square root of each side. Simplify. Answer: The geometric mean is 10.

Example 1 b: Find the geometric mean between 25 and 7. Let x represent the geometric mean. Definition of geometric mean Cross products Take the positive square root of each side. Simplify. Use a calculator. Answer: The geometric mean is about 13. 2.

Your Turn: a. Find the geometric mean between 3 and 12. Answer: 6 b. Find the geometric mean between 4 and 20. Answer: 8. 9
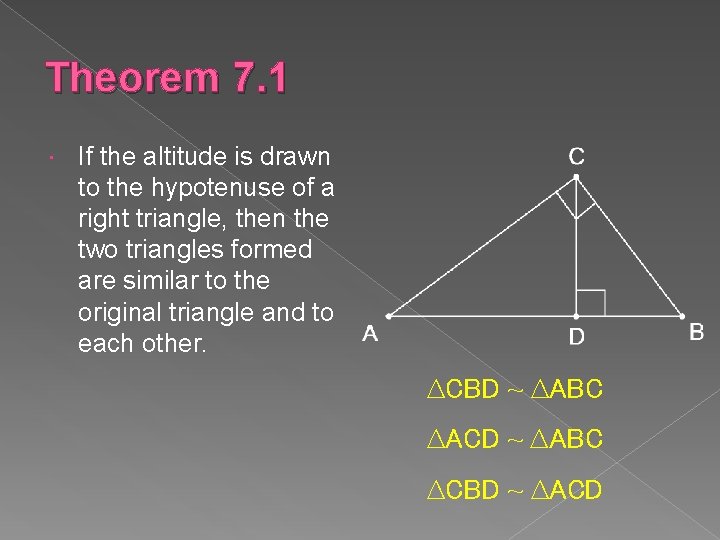
Theorem 7. 1 If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other. ∆CBD ~ ∆ABC ∆ACD ~ ∆ABC ∆CBD ~ ∆ACD

Geometric Mean Theorems Theorem 7. 2: In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The length of the altitude is the geometric mean of the lengths of the two segments. Theorem 7. 3: In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg. BD CD = CD AD AB CB = CB DB AB AC = AC AD

What does all this mean? 6 x √ 9 ∙ √ 2 = x 5+2 = y 7 = y 14 = y 2 3 √ 2 = x √ 14 = y x = 18 = x 2 √ 18 = x 3 y 2

Example 2:

Example 2: Cross products Take the positive square root of each side. Use a calculator. Answer: CD is about 12. 7.
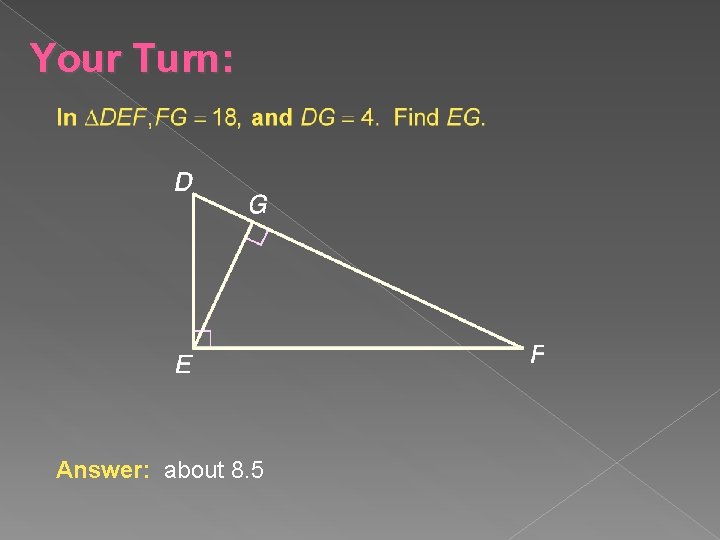
Your Turn: Answer: about 8. 5

Example 3: Cross products Divide each side by 7. 25. Answer: The length of the long rod is 7. 25 + 25. 2, or about 32. 4 inches long.
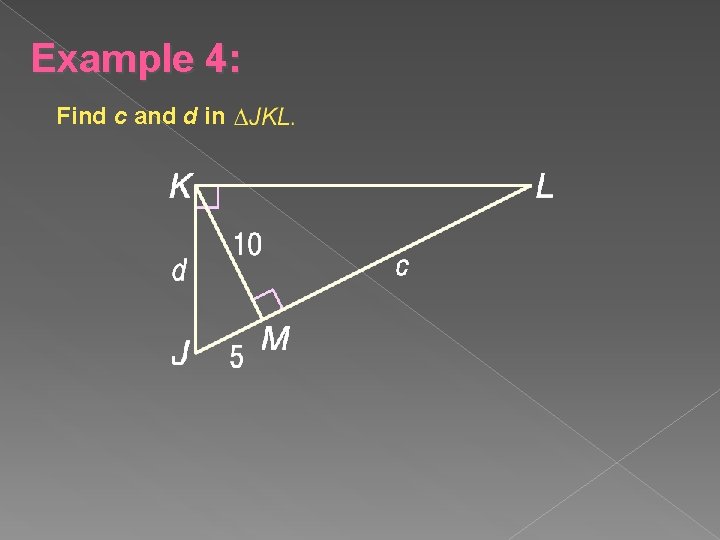
Example 4: Find c and d in

Example 4: is the altitude of right triangle JKL. Use Theorem 7. 2 to write a proportion. Cross products Divide each side by 5.

Example 4: is the leg of right triangle JKL. Use the Theorem 7. 3 to write a proportion. Cross products Take the square root. Simplify. Use a calculator. Answer:
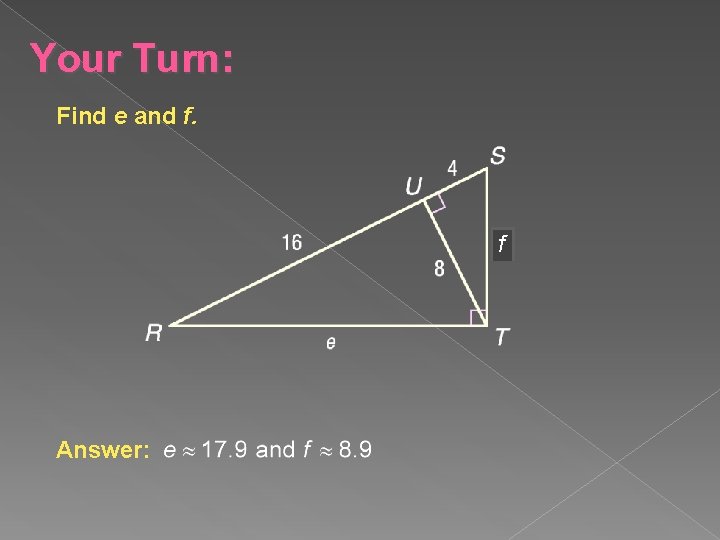
Your Turn: Find e and f. f Answer:
- Slides: 17