6162010 Parallel Patterns Reduce Scan PARALLEL PATTERNS REDUCE





























- Slides: 34

6/16/2010 Parallel Patterns - Reduce & Scan PARALLEL PATTERNS REDUCE & SCAN 1

6/16/2010 Parallel Patterns - Reduce & Scan 2 Programming Patterns For Parallelism • Some patterns repeat in many different contexts • e. g. Search an element in an array • Identifying such patterns important • Solve a problem once and reuse the solution • Split a hard problem into individual problems • Helps define interfaces

6/16/2010 Parallel Patterns - Reduce & Scan 3 We Have Already Seen Some Patterns

6/16/2010 Parallel Patterns - Reduce & Scan 4 We Have Already Seen Some Patterns • Divide and Conquer • Split a problem into n sub problems • Recursively solve the sub problems • And merge the solution • Data Parallelism • Apply the same function to all elements in a collection, array • Parallel. For, Parallel. For. Each • Also called as “map” in functional programming

6/16/2010 5 Parallel Patterns - Reduce & Scan Map • Given a function f : (A) => B • A collection a: A[] • Generates a collection b: B[], where B[i] = f( A[i] ) A f f f f B • Parallel. For, Paralle. For. Each • Where each loop iteration is independent f

6/16/2010 Parallel Patterns - Reduce & Scan 6 Reduce And Scan • In practice, parallel loops have to work together to generate an answer • Reduce and Scan patterns capture common cases of processing results of Map

6/16/2010 Parallel Patterns - Reduce & Scan 7 Reduce And Scan • In practice, parallel loops have to work together to generate an answer • Reduce and Scan patterns capture common cases of processing results of Map • Note: Map and Reduce are similar to but not the same as Map. Reduce • Map. Reduce is a framework for distributed computing

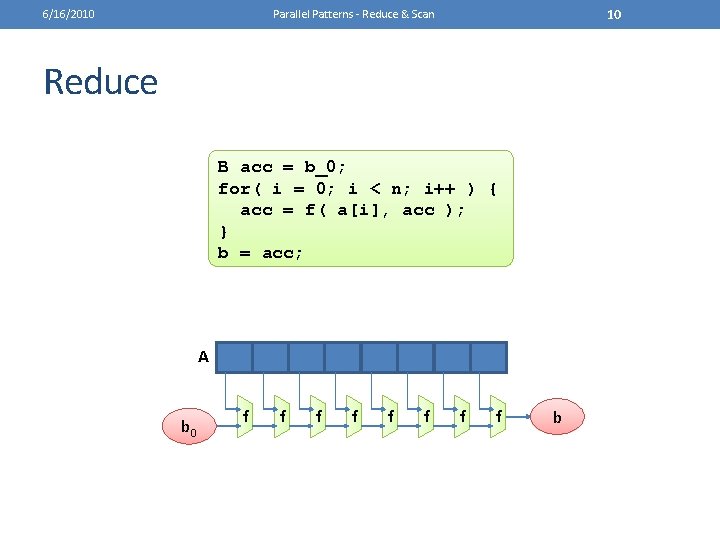
6/16/2010 8 Parallel Patterns - Reduce & Scan Reduce • Given a function f: (A, B) => B • A collection a: A[] • An initial value b 0: B • Generate a final value b: B • Where b = f(A[n-1], … f(A[1], f(A[0], b 0)) ) A b 0 f f f f b

6/16/2010 9 Parallel Patterns - Reduce & Scan Reduce • Given a function f: (A, B) => B • A collection a: A[] • An initial value b 0: B • Generate a final value b: B • Where b = f(A[n-1], … f(A[1], f(A[0], b 0)) ) A b 0 f f f f b • Only consider where A and B are the same type

6/16/2010 10 Parallel Patterns - Reduce & Scan Reduce B acc = b_0; for( i = 0; i < n; i++ ) { acc = f( a[i], acc ); } b = acc; A b 0 f f f f b

6/16/2010 Parallel Patterns - Reduce & Scan Associativity of the Reduce function • Reduce is parallelizable if f is associative f(a, f(b, c)) = f(f(a, b), c) • E. g. Addition : (a + b) + c = a + (b + c) • Where + is integer addition (with modulo arithmetic) • But not when + is floating point addition 11

6/16/2010 Parallel Patterns - Reduce & Scan Associativity of the Reduce function • Reduce is parallelizable if f is associative f(a, f(b, c)) = f(f(a, b), c) • E. g. Addition : (a + b) + c = a + (b + c) • Where + is integer addition (with modulo arithmetic) • But not when + is floating point addition • Max, min, multiply, … • Set union, intersection, 12

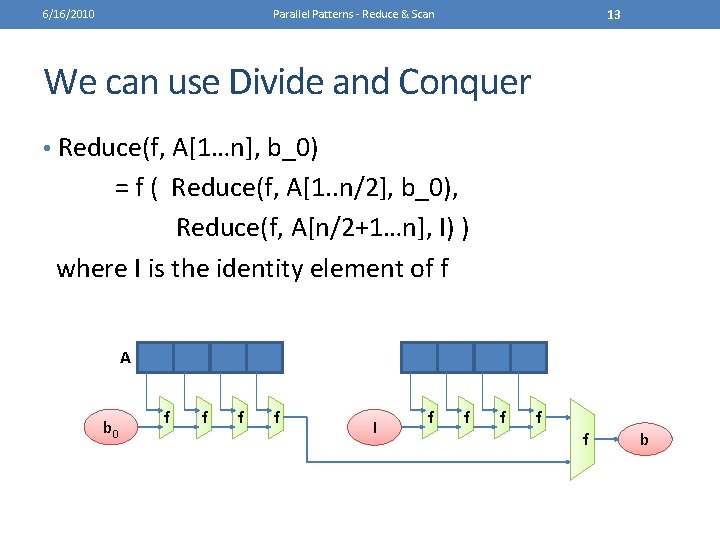
6/16/2010 13 Parallel Patterns - Reduce & Scan We can use Divide and Conquer • Reduce(f, A[1…n], b_0) = f ( Reduce(f, A[1. . n/2], b_0), Reduce(f, A[n/2+1…n], I) ) where I is the identity element of f A b 0 f f I f f f b

6/16/2010 Parallel Patterns - Reduce & Scan 14 Implementation Optimizations • Switch to sequential Reduce for the base k elements • Do k way splits instead of two way splits • Maintain a thread-local accumulated value • A task updates the value of the thread it executes in

6/16/2010 Parallel Patterns - Reduce & Scan 15 Implementation Optimizations • Switch to sequential Reduce for the base k elements • Do k way splits instead of two way splits • Maintain a thread-local accumulated value • A task updates the value of the thread it executes in • Requires that the reduce function is also commutative f(a, b) = f(b, a)

6/16/2010 Parallel Patterns - Reduce & Scan 16 Implementation Optimizations • Switch to sequential Reduce for the base k elements • Do k way splits instead of two way splits • Maintain a thread-local accumulated value • A task updates the value of the thread it executes in • Requires that the reduce function is also commutative f(a, b) = f(b, a) • Thread local values are then merged in a separate pass

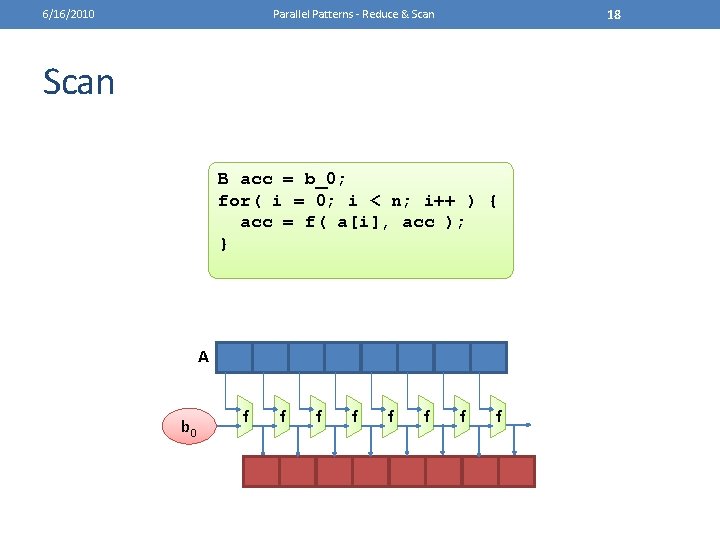
6/16/2010 17 Parallel Patterns - Reduce & Scan • Given a function f: (A, B) => B • A collection a: A[] • An initial value b 0: B • Generate a collection b: B[] • Where b[i] = f(A[i-1], … f(A[1], f(A[0], b 0)) ) A b 0 f f f f

6/16/2010 18 Parallel Patterns - Reduce & Scan B acc = b_0; for( i = 0; i < n; i++ ) { acc = f( a[i], acc ); } A b 0 f f f f

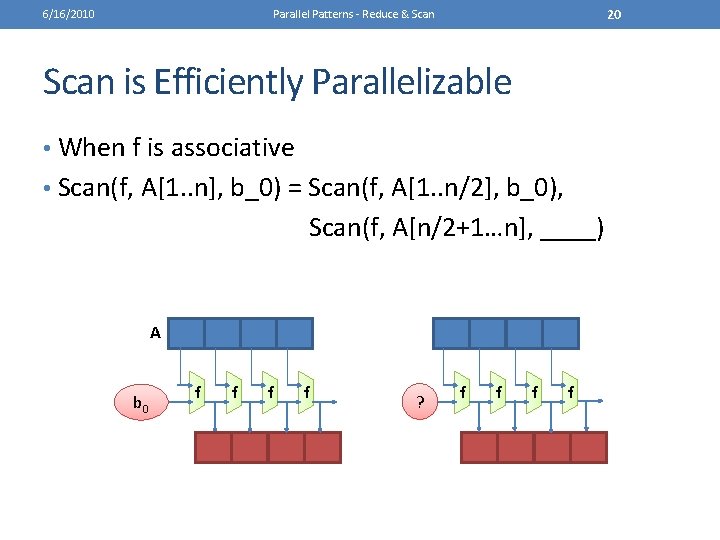
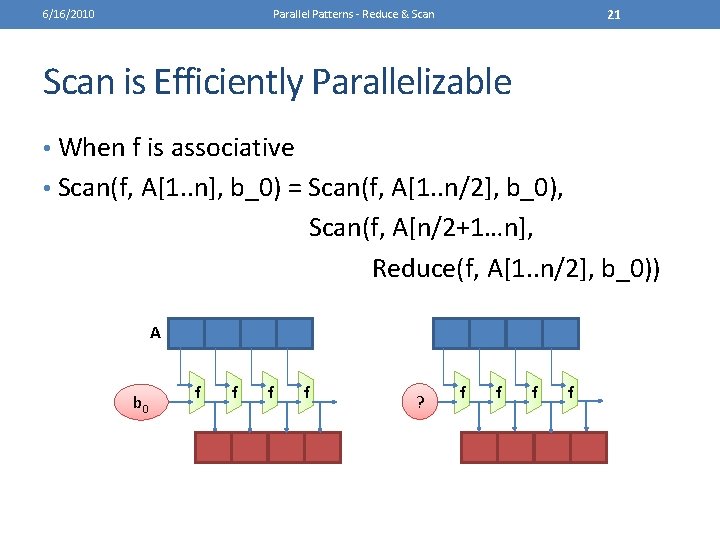
6/16/2010 Parallel Patterns - Reduce & Scan is Efficiently Parallelizable • When f is associative 19

6/16/2010 20 Parallel Patterns - Reduce & Scan is Efficiently Parallelizable • When f is associative • Scan(f, A[1. . n], b_0) = Scan(f, A[1. . n/2], b_0), Scan(f, A[n/2+1…n], ____) A b 0 f f ? f f

6/16/2010 21 Parallel Patterns - Reduce & Scan is Efficiently Parallelizable • When f is associative • Scan(f, A[1. . n], b_0) = Scan(f, A[1. . n/2], b_0), Scan(f, A[n/2+1…n], Reduce(f, A[1. . n/2], b_0)) A b 0 f f ? f f

6/16/2010 Parallel Patterns - Reduce & Scan is useful in many places • Radix Sort • Ray Tracing • … 22

6/16/2010 Parallel Patterns - Reduce & Scan is useful in many places • Radix Sort ( ) • Ray Tracing • … 23

6/16/2010 Parallel Patterns - Reduce & Scan Computing Line of Sight • Given x 1, … xn with altitudes a[1], …a[n] • Which of the points are visible from x 0 24

6/16/2010 Parallel Patterns - Reduce & Scan 25 Computing Line of Sight • Given x 0, … xn with altitudes alt[0], …alt[n] • Which of the points are visible from x 0 • angle[i] = arctan( (alt[i] – alt[0]) / i ) • xi is visible from x 0 if all points between them have lesser angle than angle[i]

6/16/2010 Solution Parallel Patterns - Reduce & Scan 26

6/16/2010 Radix Sort 5 = 101 7 = 111 2 = 010 4 = 100 5 = 101 3 = 011 1 = 001 Parallel Patterns - Reduce & Scan 27

6/16/2010 Parallel Patterns - Reduce & Scan Radix Sort 5 = 101 2 = 010 7 = 111 4 = 100 2 = 010 5 = 101 4 = 100 7 = 111 5 = 101 3 = 011 1 = 001 28

6/16/2010 Parallel Patterns - Reduce & Scan Radix Sort 5 = 101 2 = 010 4 = 100 7 = 111 4 = 100 5 = 101 2 = 010 5 = 101 4 = 100 7 = 111 1 = 001 5 = 101 2 = 010 3 = 011 7 = 111 1 = 001 3 = 011 29

6/16/2010 30 Parallel Patterns - Reduce & Scan Radix Sort 5 = 101 2 = 010 4 = 100 1 = 001 7 = 111 4 = 100 5 = 101 2 = 010 5 = 101 3 = 011 4 = 100 7 = 111 1 = 001 4 = 100 5 = 101 2 = 010 5 = 101 3 = 011 7 = 111 5 = 101 1 = 001 3 = 011 7 = 111

6/16/2010 Parallel Patterns - Reduce & Scan 31 Basic Primitive: Pack • Given an array A and an array F of flags • A = [5 7 2 4 5 3 1] • F = [1 1 0 0 1 1 1] • Pack all elements with flag = 0 before elements with flag = 1 • A’ = [2 4 5 7 5 3 1]

6/16/2010 Solution Parallel Patterns - Reduce & Scan 32

6/16/2010 Parallel Patterns - Reduce & Scan Other Applications of Scan • Radix Sort • Computing Line of Sight • Adding multi-precision numbers • Quick Sort • To search for regular expressions • Parallel grep • … 33

6/16/2010 Parallel Patterns - Reduce & Scan High Level Points • Minimize dependence between parallel loops • Unintended dependences = data races • Next lecture • Carefully analyze remaining dependences • Use Reduce and Scan patterns where applicable 34