6 Work Energy Power 1 2 3 4

6. Work, Energy & Power 1. 2. 3. 4. Work Forces that Vary Kinetic Energy Power

Does the work of climbing a mountain depend on the route chosen? No Direct application of Newton’s law can be infeasible. What’s the speed of these skiers at the bottom of the slope? simple complicated Energy conservation to the rescue (Chap 7).

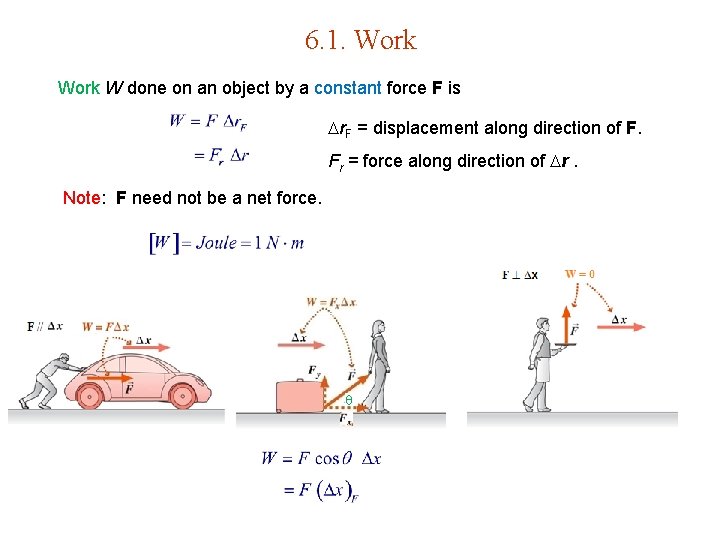
6. 1. Work W done on an object by a constant force F is r. F = displacement along direction of F. Fr = force along direction of r. Note: F need not be a net force.

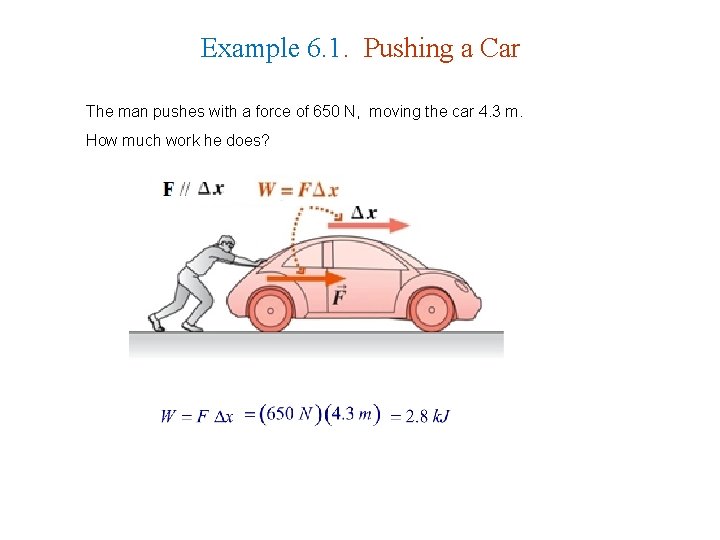
Example 6. 1. Pushing a Car The man pushes with a force of 650 N, moving the car 4. 3 m. How much work he does?

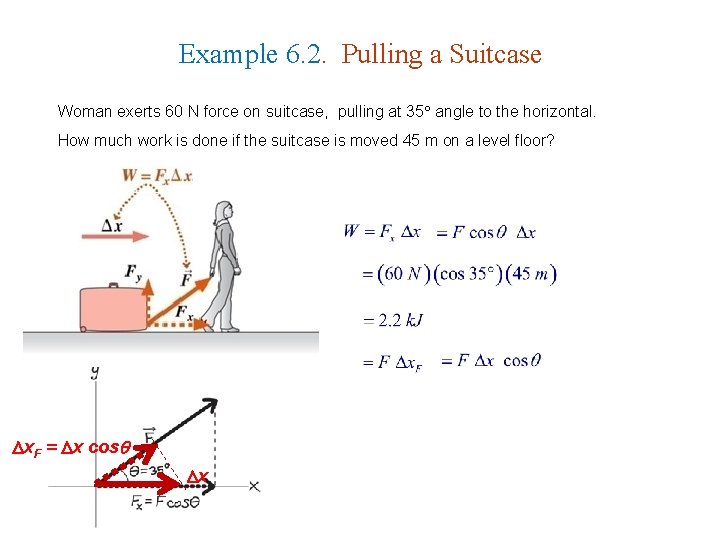
Example 6. 2. Pulling a Suitcase Woman exerts 60 N force on suitcase, pulling at 35 angle to the horizontal. How much work is done if the suitcase is moved 45 m on a level floor? x. F = x cos x

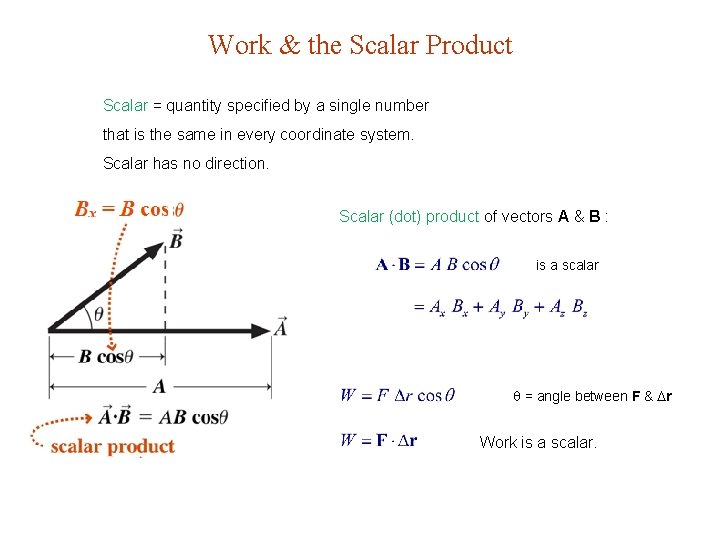
Work & the Scalar Product Scalar = quantity specified by a single number that is the same in every coordinate system. Scalar has no direction. Scalar (dot) product of vectors A & B : is a scalar = angle between F & r Work is a scalar.

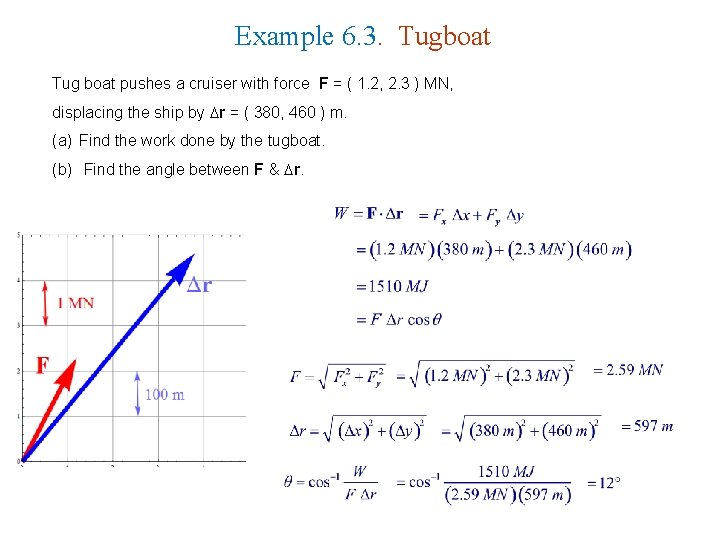
Example 6. 3. Tugboat Tug boat pushes a cruiser with force F = ( 1. 2, 2. 3 ) MN, displacing the ship by r = ( 380, 460 ) m. (a) Find the work done by the tugboat. (b) Find the angle between F & r.

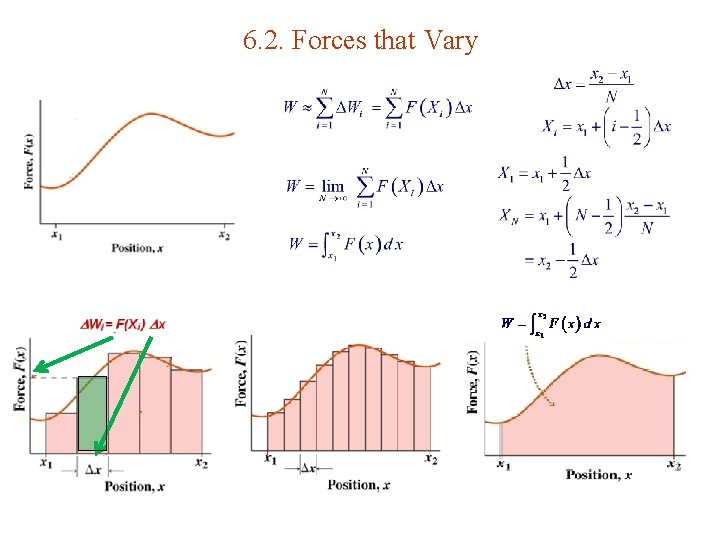
6. 2. Forces that Vary

Tactics 6. 1. Integrating Example: Since we have See Appendix A for integral table.

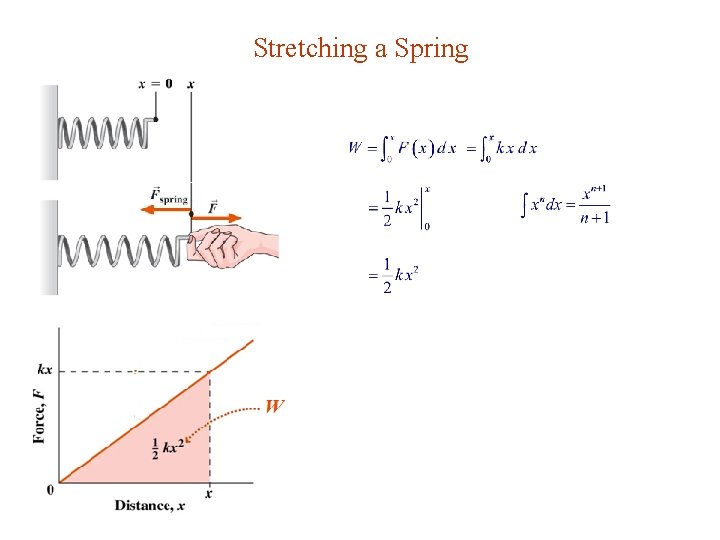
Stretching a Spring

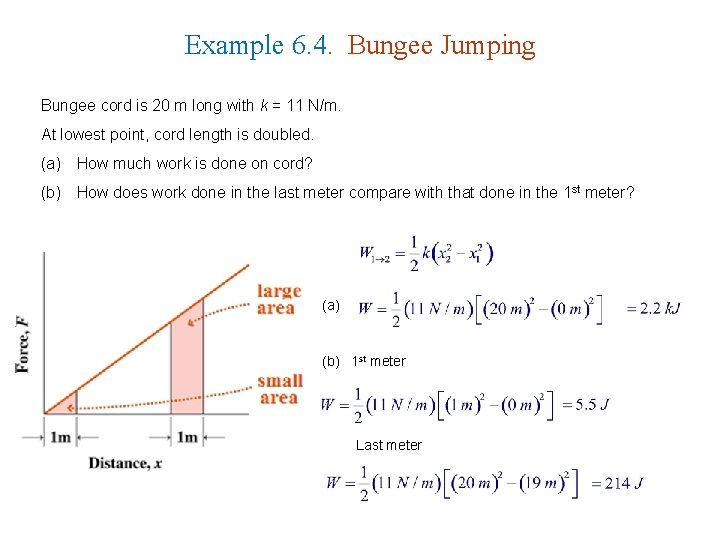
Example 6. 4. Bungee Jumping Bungee cord is 20 m long with k = 11 N/m. At lowest point, cord length is doubled. (a) How much work is done on cord? (b) How does work done in the last meter compare with that done in the 1 st meter? (a) (b) 1 st meter Last meter

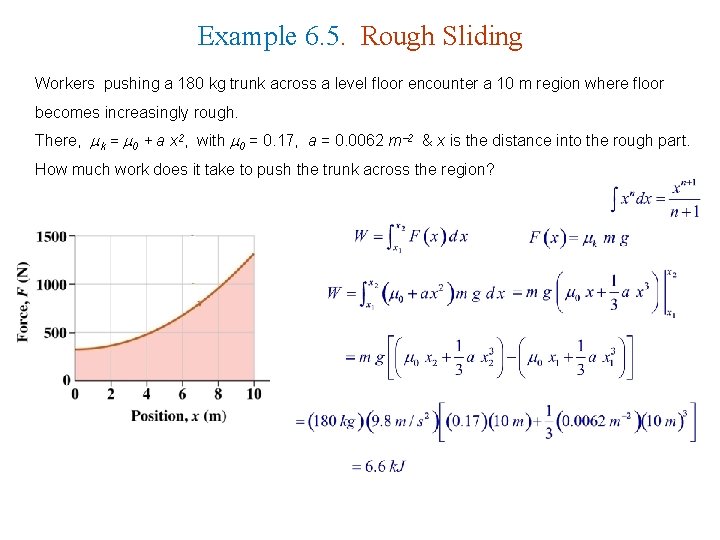
Example 6. 5. Rough Sliding Workers pushing a 180 kg trunk across a level floor encounter a 10 m region where floor becomes increasingly rough. There, k = 0 + a x 2, with 0 = 0. 17, a = 0. 0062 m 2 & x is the distance into the rough part. How much work does it take to push the trunk across the region?

Force & Work in 2 - & 3 - D Line integral

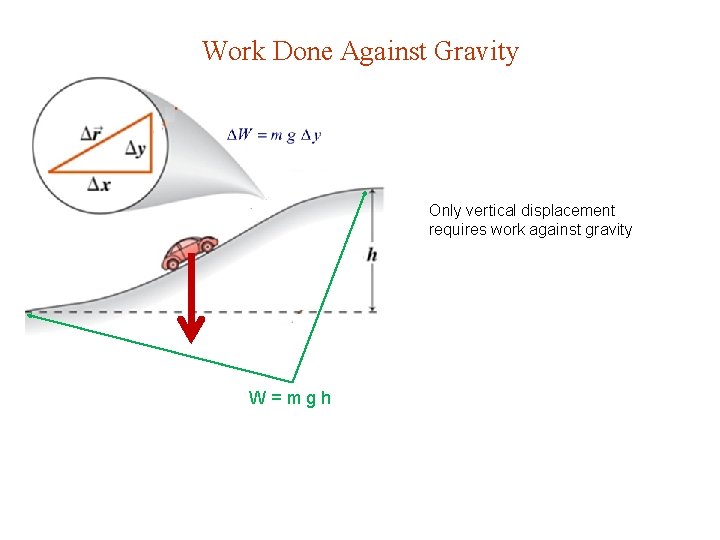
Work Done Against Gravity Only vertical displacement requires work against gravity W=mgh

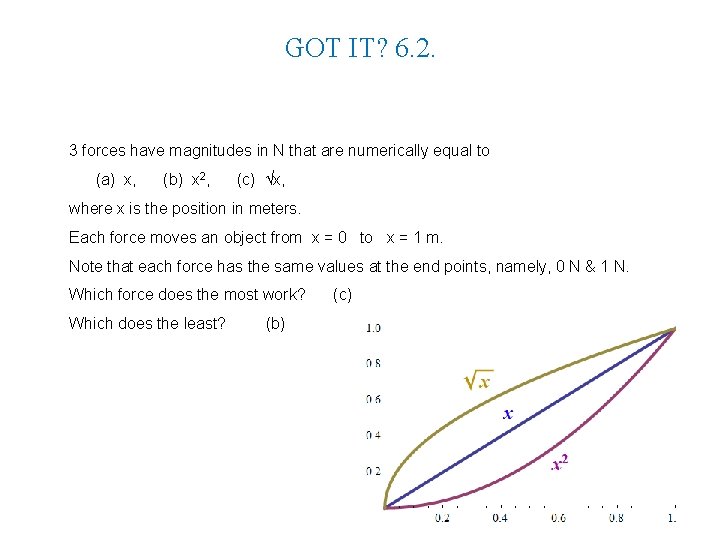
GOT IT? 6. 2. 3 forces have magnitudes in N that are numerically equal to (a) x, (b) x 2, (c) x, where x is the position in meters. Each force moves an object from x = 0 to x = 1 m. Note that each force has the same values at the end points, namely, 0 N & 1 N. Which force does the most work? Which does the least? (b) (c)

6. 3. Kinetic Energy Kinetic energy: K is relative (depends on reference frame). K is a scalar. Work-energy theorem:

Example 6. 6. Passing Zone A 1400 kg car enters a passing zone & accelerates from 70 to 95 km/h. (a) How much work is done on the car? (b) If the car then brakes to stop, how much work is done on it? (a) b)

GOT IT? 6. 3. For each situation, tell whether the net work done on a soccer ball is positive, negative, or zero. Justify your answer using the work-energy theorem. (a) You carry the ball to the field, walking at constant speed. zero ( K=0) (b) You kick the stationary ball, starting it flying through the air. positive ( K>0) (c) negative ( K<0) The ball rolls along the filed, gradually coming to a halt.

Energy Units [energy] = [work] = J (SI) CGS: Other energy units: e. V (electron-volt): used in nuclear, atomic, molecular, solid state physics. cal (calorie), BTU (British Thermal Unit): used in thermodynamics. k. W-h (kilowatt-hours): used in engineering. See Appendix C

6. 4. Power Average power: (Instantaneous) power: Example 6. 7. Climbing Mount Washington A 55 kg hiker makes the vertical rise of 1300 m in 2 h. A 1500 kg car takes ½ h to go there. Neglecting loss to friction, what is the average power output for each. Hiker: Car:

for constant power P general case Example 6. 8. Yankee Stadium Each of the 500 floodlights at Yankee stadium uses 1. 0 k. W power. How much do they cost for a 4 h night game, if electricity costs 9. 5 ₵ / k. W-h ?

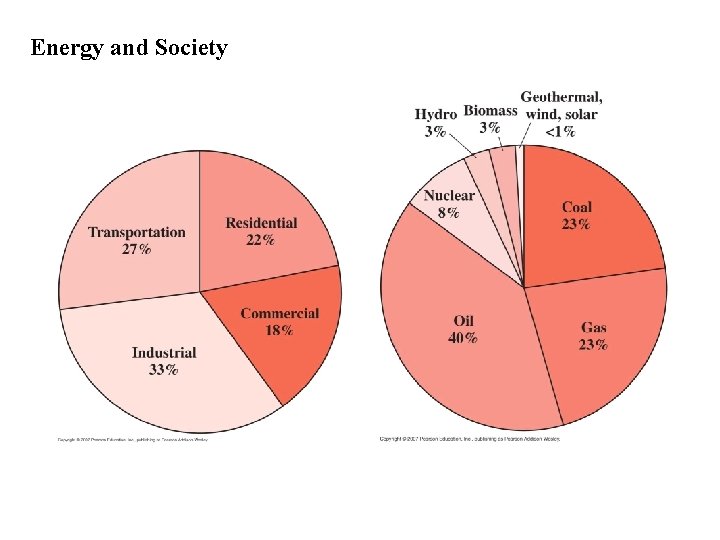
Energy and Society

Power & Velocity Example 6. 9. Bicycling Fair v Riding a 14 kg bicycle at a steady 18 km/h (5. 0 m/s), you experience a 30 N force from air resistance. If you mass 68 kg, what power must you supply (a) on level ground. Fair v (b) up a 5 slope. (a) (b) Fg