6 Trigonometry Copyright Cengage Learning All rights reserved

6 Trigonometry Copyright © Cengage Learning. All rights reserved.

6. 1 Angles and Their Measures Copyright © Cengage Learning. All rights reserved.

Objectives Describe angles. Use degree measure. Use radian measure. Convert between degrees and radians. Use angles to model and solve real-life problems. 3

Angles 4

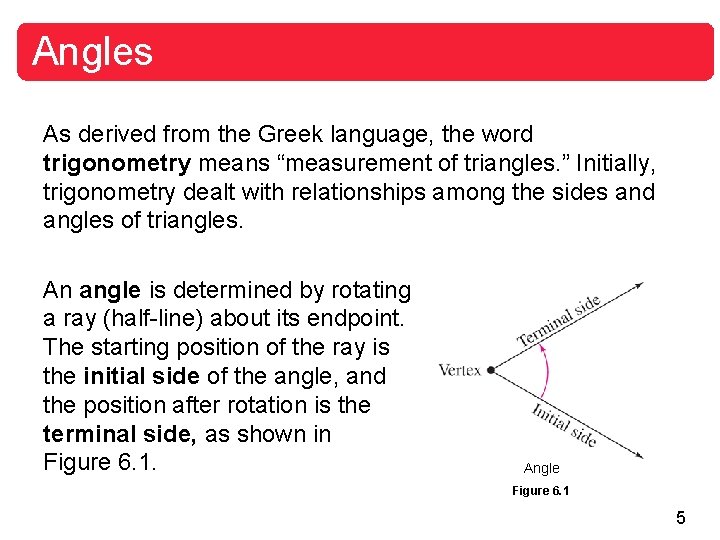
Angles As derived from the Greek language, the word trigonometry means “measurement of triangles. ” Initially, trigonometry dealt with relationships among the sides and angles of triangles. An angle is determined by rotating a ray (half-line) about its endpoint. The starting position of the ray is the initial side of the angle, and the position after rotation is the terminal side, as shown in Figure 6. 1. Angle Figure 6. 1 5

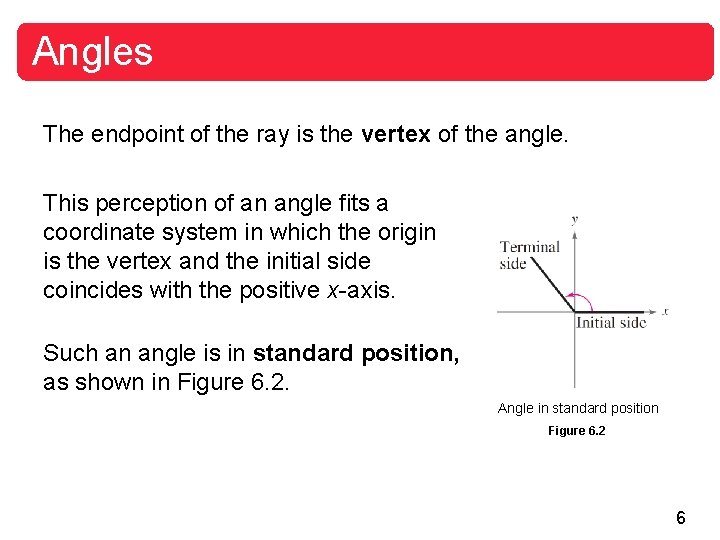
Angles The endpoint of the ray is the vertex of the angle. This perception of an angle fits a coordinate system in which the origin is the vertex and the initial side coincides with the positive x-axis. Such an angle is in standard position, as shown in Figure 6. 2. Angle in standard position Figure 6. 2 6

Angles Positive angles are generated by counterclockwise rotation, and negative angles by clockwise rotation, as shown in Figure 6. 3 Angles are labeled with Greek letters (alpha), (beta), and (theta), as well as uppercase letters A, B, and C. 7

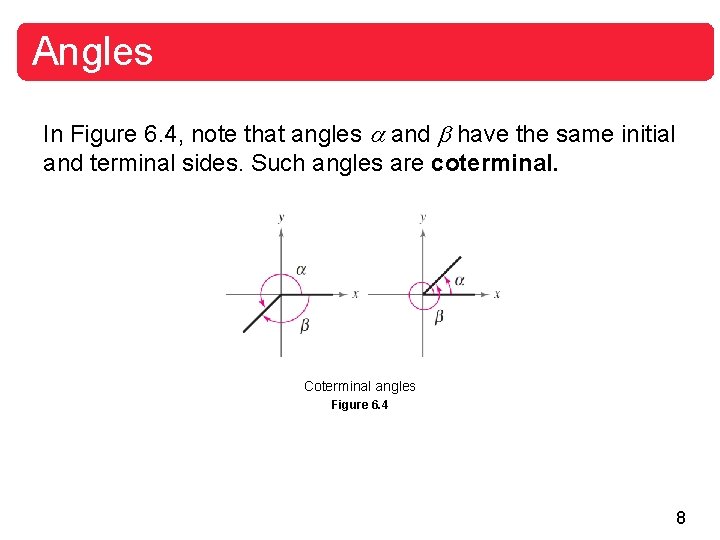
Angles In Figure 6. 4, note that angles and have the same initial and terminal sides. Such angles are coterminal. Coterminal angles Figure 6. 4 8

Degree Measure 9

Degree Measure The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. The most common unit of angle measure is the degree, denoted by the symbol . A measure of one degree (1 ) is equivalent to a rotation of of a complete revolution about the vertex. To measure angles, it is convenient to mark degrees on the circumference of a circle, as shown in Figure 6. 5 10

Degree Measure So, a full revolution (counterclockwise) corresponds to 360 , a half revolution to 180 , a quarter revolution to 90 , and so on. Recall that the four quadrants in a coordinate system are numbered I, III, and IV. Figure 6. 6 shows which angles between 0 and 360 lie in each of the four quadrants. Figure 6. 6 11

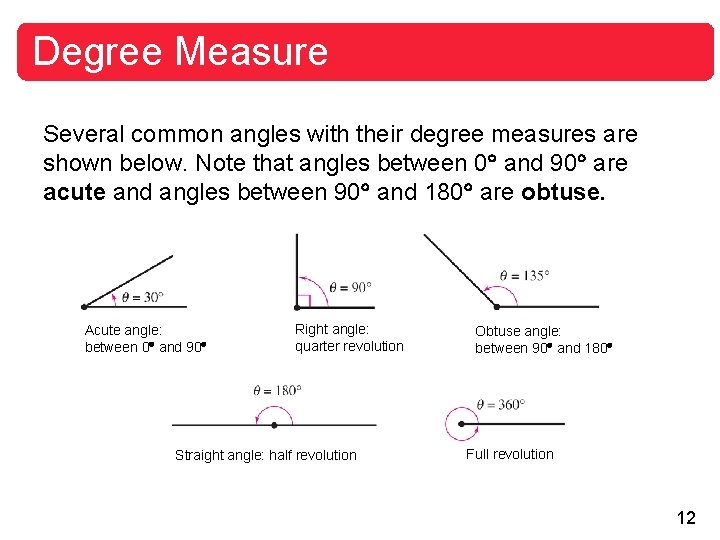
Degree Measure Several common angles with their degree measures are shown below. Note that angles between 0 and 90 are acute and angles between 90 and 180 are obtuse. Acute angle: between 0 and 90 Right angle: quarter revolution Straight angle: half revolution Obtuse angle: between 90 and 180 Full revolution 12

Degree Measure Two angles are coterminal if they have the same initial and terminal sides. For instance, the angles 0 and 360 are coterminal, as are the angles 30 and 390. You can find an angle that is coterminal to a given angle by adding or subtracting 360 (one revolution), as demonstrated in Example 1. A given angle has infinitely many coterminal angles. For instance, = 30 is coterminal with 30 + n(360 ), where n is an integer. 13

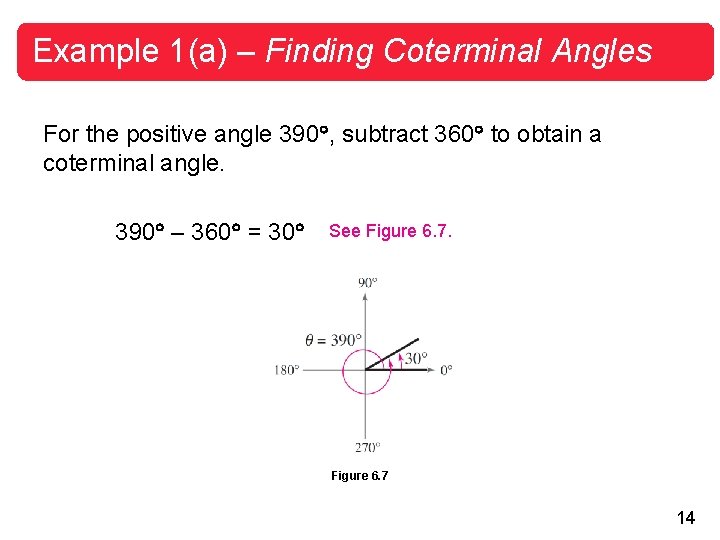
Example 1(a) – Finding Coterminal Angles For the positive angle 390 , subtract 360 to obtain a coterminal angle. 390 – 360 = 30 See Figure 6. 7 14

Example 1(b) – Finding Coterminal Angles cont’d For the positive angle 135 , subtract 360 to obtain a coterminal angle. 135 – 360 = – 225 See Figure 6. 8 15

Example 1(c) – Finding Coterminal Angles cont’d For the negative angle – 120 , add 360 to obtain a coterminal angle. – 120 + 360 = 240 See Figure 6. 9 16

Degree Measure Two positive angles and are complementary (complements of each other) when their sum is 90. Two positive angles are supplementary (supplements of each other) when their sum is 180. (See below. ) Complementary angles Supplementary angles 17

Radian Measure 18

Radian Measure A second way to measure angles is in radians. This type of measure is especially useful in calculus. To define a radian, you can use a central angle of a circle, one whose vertex is the center of the circle, as shown in Figure 6. 10. Arc length = radius when = 1 radian Figure 6. 10 19

Radian Measure Because the circumference of a circle is 2 r units, it follows that a central angle of one full revolution (counterclockwise) corresponds to an arc length of s = 2 r. 20

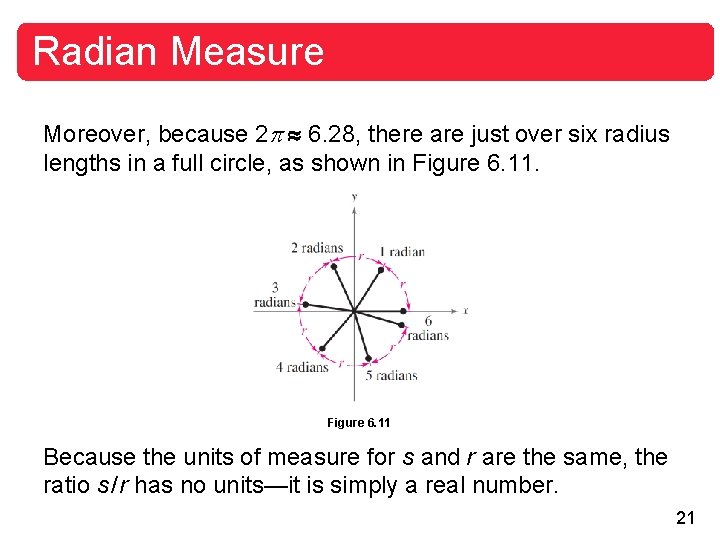
Radian Measure Moreover, because 2 6. 28, there are just over six radius lengths in a full circle, as shown in Figure 6. 11 Because the units of measure for s and r are the same, the ratio s / r has no units—it is simply a real number. 21

Example 3 – Finding Angles Find a. the complement of = / 12, b. the supplement of = 5 / 6, and c. a coterminal angle to = 17 / 6. 22

Example 3(a) – Solution In radian measure, the complement of an angle is found by subtracting the angle from / 2, which is equivalent to 90. So, the complement of = / 12 is ( / 2) – ( / 12) = (6 / 12) – ( / 12) = 5 / 12. See Figure 6. 12 23

Example 3(b) – Solution cont’d In radian measure, the supplement of an angle is found by subtracting the angle from , which is equivalent to 180. So, the supplement of = 5 / 6 is – (5 / 6) = (6 / 6) – (5 / 6) = / 6. See Figure 6. 13 24

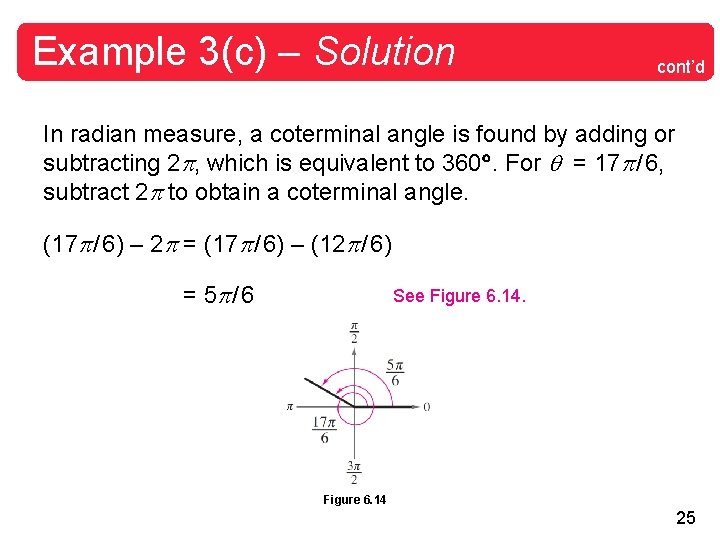
Example 3(c) – Solution cont’d In radian measure, a coterminal angle is found by adding or subtracting 2 , which is equivalent to 360. For = 17 / 6, subtract 2 to obtain a coterminal angle. (17 / 6) – 2 = (17 / 6) – (12 / 6) = 5 / 6 See Figure 6. 14 25

Conversion of Angle Measure 26

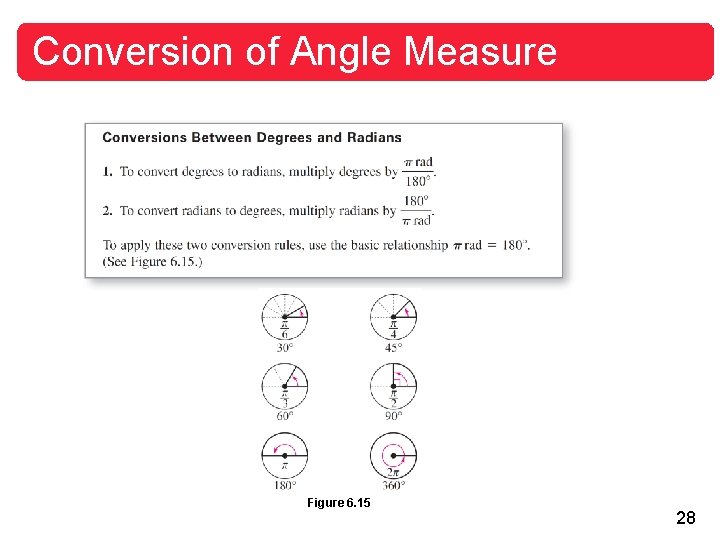
Conversion of Angle Measure Because 2 radians corresponds to one complete revolution, degrees and radians are related by the equations 360 = 2 rad and 180 = rad. From the latter equation, you obtain and which lead to the following conversion rules. 27

Conversion of Angle Measure Figure 6. 15 28

Conversion of Angle Measure When no units of angle measure are specified, radian measure is implied. For instance, = 2 implies that = 2 radians. 29

Example 4 – Converting from Degrees to Radians a. b. Multiply by 30

Applications 31

Applications The radian measure formula, = s / r, can be used to measure arc length along a circle. 32

Applications The formula for the length of a circular arc can be used to analyze the motion of a particle moving at a constant speed along a circular path. 33

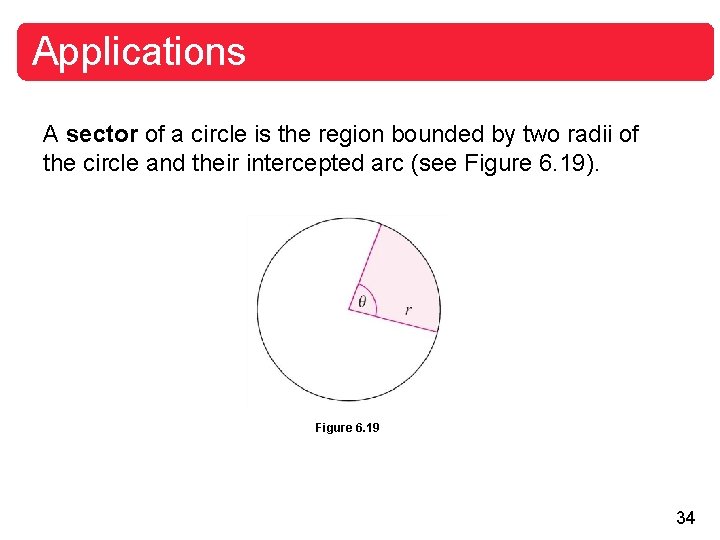
Applications A sector of a circle is the region bounded by two radii of the circle and their intercepted arc (see Figure 6. 19). Figure 6. 19 34

Applications 35

Example 9 – Area of a Sector of a Circle A sprinkler on a golf course fairway sprays water over a distance of 70 feet and rotates through an angle of 120 (see Figure 6. 20). Find the area of the fairway watered by the sprinkler. Figure 6. 20 36

Example 9 – Solution First convert 120 to radian measure as follows. = 120 Multiply by Then, using = 2 /3 and r = 70, the area is Formula for the area of a sector of a circle. 37

Example 9 – Solution cont’d Substitute for r and . Multiply. Simplify. 38