6 Symmetry 6 A The Translation Operator Definition

6. Symmetry 6 A. The Translation Operator Definition and Simple Properties • The translation operator T(a) is defined as • Easy things to prove: • We previously showed that it is unitary • It also follows that • What does it do to wave functions?

Translation of Position and Momentum • Do P or R commute with T(a)? • Multiply on the left by T†(a) • Translation shifts R but leaves P unchanged • We can figure out how translation affects any combination of R and P – Insert 1 = T (a)T† (a) as needed

Sample Problem Suppose we have What is T†(a)HT(a)? • Generalizing:

Problems Related by Translation Suppose two Hamiltonians are related by a translation operation, . Then they will have the same eigenvalues and their eigenvectors are related by. • The | ’n ’s are eigenstates of H’: • We therefore have: • In general, • Use this to make problems easier

Sample Problem • Complete the square: What are the eigenvalues and eigenstates of • Now shift the potential: • H’ is Harmonic oscillator plus energy shift • Same energies, but shifted eigenstates:

6 B. The Rotation Operator Rotation Matrices • A rotation is a linear mapping of the position coordinates that preserves the distance from the origin: • Distance from origin stays the same: • is an orthogonal matrix (real and unitary) • Take determinant of 1 = T : • Proper rotations have det( ) =1 and can be physically performed – Like rotation about an axis • Improper rotations have det( ) = -1 and can’t be physically performed – Like reflection in a mirror • We’ll focus only on proper rotations for now

Rotations in 2 D and 3 D • It is impossible to have a proper rotation in 1 D • In 2 D, you can only rotate in the XY- plane – Parameterized by a single angle • In 3 D, you can rotate around any axis – Parameterized by a direction and an angle • We will concentrate on rotations around one of the three axes x, y, z • In 4 D and higher, it gets worse – We won’t go there – You’re welcome

Definition of Rotation Operator, and Properties • For any rotation operator , define the rotation operator R( ) as: • Easy things to prove: • Let’s prove one: • It’s also unitary: • It also follows that • It rotates wave functions

Rotation of Position and Momentum • Do P or R commute with R( )? • Multiply on the left by R†( ) • Rotations rotates both R and P • We can figure out how translation affects any combination of R and P – Insert 1 = R ( )R† ( ) as needed

Problems Related by Rotation Suppose two Hamiltonians are related by a rotation operation, . Then they will have the same eigenvalues and their eigenvectors are related by. • The | ’n ’s are eigenstates of H’: • We therefore have: • The kinetic term is unaffected by rotation: • The potential term becomes: • We therefore have

Sample Problem • Allowed region: • Rotate by 45 Find the eigenstates and eigenenergies of a particle of mass m in a 2 D potential • Our rotated coordinates are • Allowed region becomes • The modified Hamiltonian is • This is just a shifted 2 D infinite square well

Sample Problem (2) Find the eigenstates and eigenenergies of a particle of mass m in a 2 D potential • Now shift: • Eigenstate and energies for this are well known • The original problem has same energies, and eigenstates

Parity • • Define parity, at least for an odd number of dimensions, as In an odd number of dimensions, this is an improper rotation All improper rotations are a combination of parity and a proper rotation Easy to show that: • Do all vector quantities work like this? Consider angular momentum: • Vectors that behave like R or P are sometimes called true vectors • Those that behave like L called pseudovectors or axial vectors • You can similarly distinguish between true scalars and pseudoscalars • Under parity, the Hamiltonian transforms to

6 C. Solving Problems Using Parity Helps Find Eigenstates • We note that for the Harmonic oscillator: – Is this something special about the H. O. ? • Note that • We therefore have • Two operators that commute can be simultaneously diagonalized: • Parity, like all symmetries, is a unitary operator – It therefore has eigenvalues of magnitude 1 • For the case of parity, we can simplify it even further: • When parity is a symmetry of H, eigenstates will have either

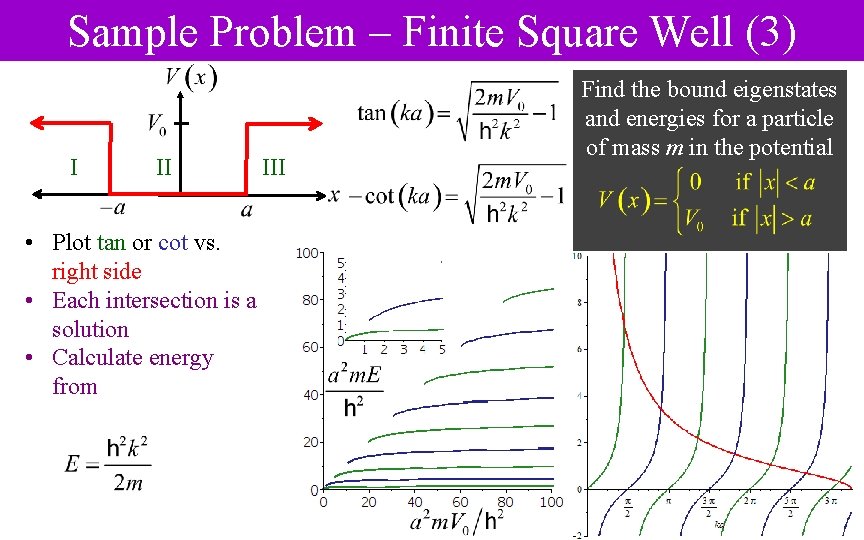
Sample Problem – Finite Square Well I II III Find the bound eigenstates and energies for a particle of mass m in the potential • Bound states have E < V 0 but will have E > 0 • Need to solve Schrödinger separately in each of three regions • To keep the solutions well-behaved, most general solution is then • By parity, eigenstates can be chosen odd or even

Sample Problem – Finite Square Well (2) I II III Find the bound eigenstates and energies for a particle of mass m in the potential Even case: (–x) = (x) • This relates region I to region III and region II to itself • Match wave function and its derivative at x = a: • Substitute the first equation in the second Odd case: (–x) = – (x) • Assign as a homework problem

Sample Problem – Finite Square Well (3) I II • Plot tan or cot vs. right side • Each intersection is a solution • Calculate energy from III Find the bound eigenstates and energies for a particle of mass m in the potential

6 D. Discrete Rotations and Eigenvalues • • • Say our Hamiltonian is given by P 2 is automatically invariant under rotations Suppose V(R) is also invariant under rotation : Then H commutes with R( ) It follows that our eigenstates are like • As always, eigenvalues of unitary operators have magnitude one • If m = 1 for some integer m, then: • The m’th roots of unity are given by:

Example of Discrete Rotation: • Consider a particle of mass m in 2 D in potential • Consider rotations by 90 : • Easy to see that • It follows that eigenstates of H will also be eigenstates of R( ) • Note that 4 = 1, so we must have 4 = 1 • Some example states: • Corresponding energies – note the degeneracy of the i eigenstates

Complex Eigenvalues and Degeneracy • Note that we got some degenerate energies – Is this a general feature? • Suppose we have a Hamiltonian that is real – Note that P 2 has two factors of i that cancel • Suppose we have an Eigenstate of R and H • Take the complex conjugate (not Hermitian conjugate) of these equations – Note that rotation involves no complex numbers • We see that | * is also an eigenstate of H and R( ), with the same energy but a different rotation eigenvalue (if is not real) • It follows that we have distinct states with the same energy (degeneracy) • Common feature: Symmetries lead to degenerate states

Which Rotation? • The problem we solved had four rotations that all work: • Can’t we write it as an eigenstate of each? • 0 rotation is the identity operator • Suppose it has eigenvalue under 90 rotation • We can deduce the eigenvalue under other rotations • In contrast, you can’t figure out the 90 rotation eigenvalue from the 180 rotation eigenvalue, because complex numbers have two square roots • Always use the smallest non-zero rotation

6 E. Discrete Translations The Kronig-Penney Model • Crystals consist of regular repeating patterns • Let’s study a simple 1 D example – Called the Kronig-Penney Model* • It is invariant under translation by an amount a: • Eigenstates are also eigenstates of T(a): • Because [T(a)]m 1 for any m, is unrestricted *Different things are called the Kronig-Penney model. This one’s marginally simpler than the usual versions.

The Crystal Momentum • • Instead of given the phase in terms of , we write The quantity k is then called the crystal momentum Note that ka is 2 ambiguous – we normally choose The crystal momentum allows us to translate the wave function • Substitute x x + a, then iterate • This allows us to deduce the wave function everywhere if we know it on [0, a)

Kronig-Penney Model – Within Regions • We need to solve Schrödinger’s Equation • Within region I, there is no potential: • We can use periodicity to get it in any other region: • In particular, letting x = a, we can see that • It remains to solve Schrödinger at the boundaries

Kronig-Penney Model – At the Boundary • • Integrate Schrödinger across x = a: In limit of small , left side vanishes First term on right is integral of a derivative Second term on right gets contribution only from x = a • Finite discontinuity in derivative implies continuous function • We use periodicity to rewrite these expressions

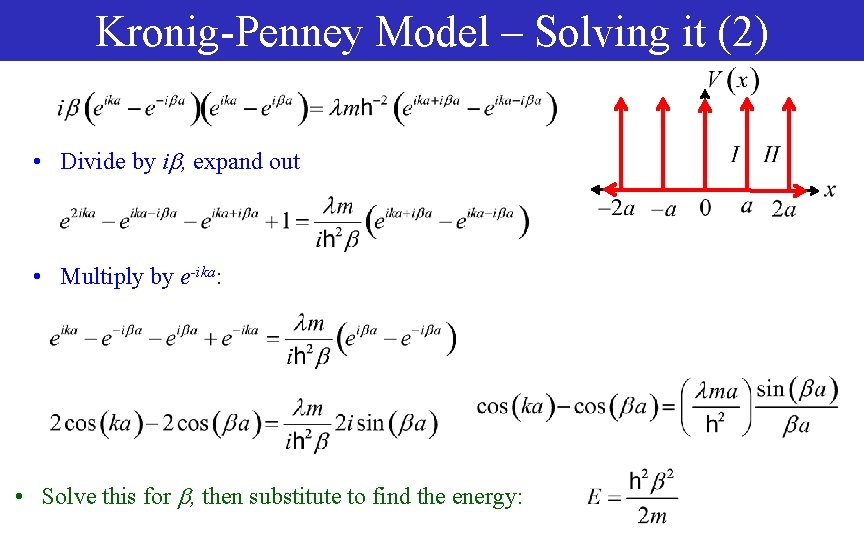
Kronig-Penney Model – Solving it (1) • Substitute in: • In each expression, gather A on one side and B on the other • Multiply these expressions together (cancel AB) • Cancel terms, divide by 2

Kronig-Penney Model – Solving it (2) • Divide by i , expand out • Multiply by e-ika: • Solve this for , then substitute to find the energy:

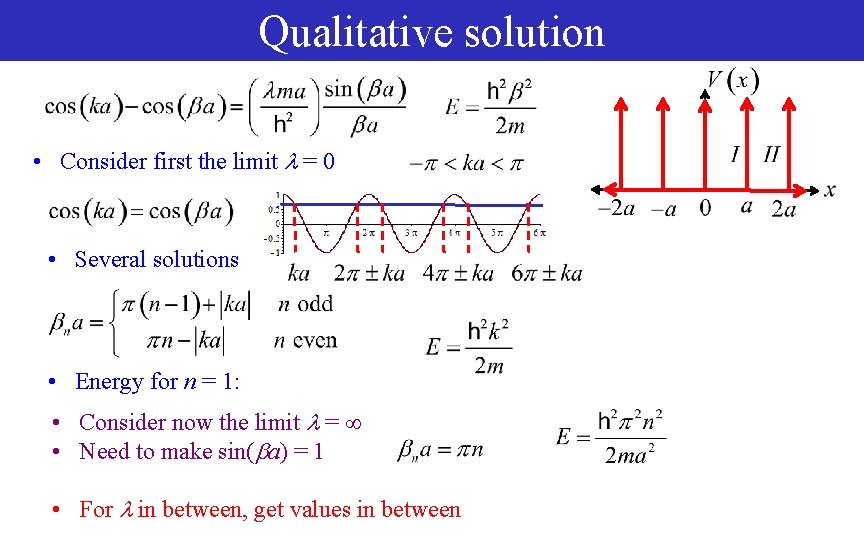
Qualitative solution • Consider first the limit = 0 • Several solutions • Energy for n = 1: • Consider now the limit = • Need to make sin( a) = 1 • For in between, get values in between

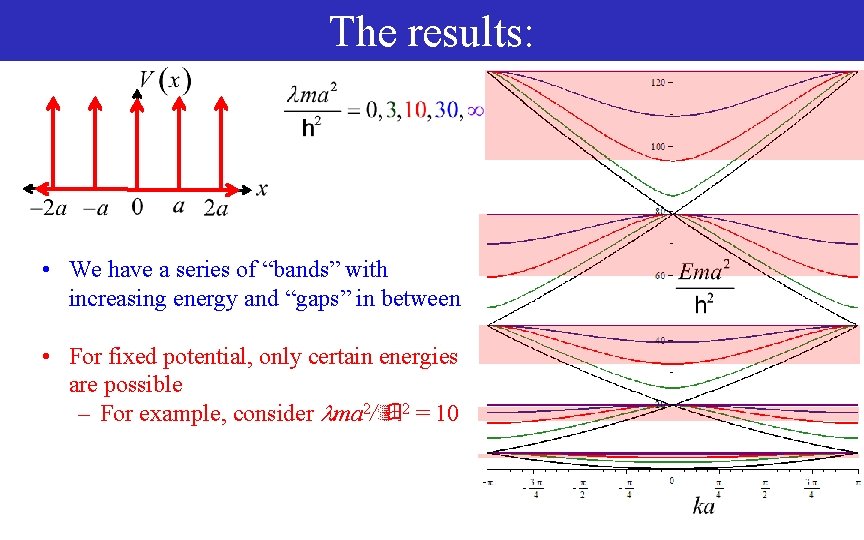
The results: • We have a series of “bands” with increasing energy and “gaps” in between • For fixed potential, only certain energies are possible – For example, consider ma 2/ 2 = 10

6 F. Continuous Symmetries and Generators Continuous Translations • Suppose a Hamiltonian invariant under arbitrary translations • We want to consider the smallest possible non-zero translation • Taylor expand T(a) for small a – Recall T(0) = 1 • Let us define, somewhat arbitrarily: • We know T is unitary • So this operator is Hermitian • What exactly is this operator?

P is the Generator of Translations • For small translations, we can approximate • Large translations can be made from many small ones: • Expand this out • Now take limit N • This can be generalized to 3 D • We say that P is the generator of translations

Continuous Rotations in 2 D • Suppose a 2 D Hamiltonian invariant under arbitrary rotations • Taylor expand R( ( )) for small • Let us define, somewhat arbitrarily: • As before, we can prove Lz is Hermitian • What exactly is this operator?

L is the Generator of Rotations • For small rotations, we can approximate • Large translations can be made from many small ones: • Now take limit N • We say that Lz is the generator of rotations

Angular Momentum in 3 D • In three dimensions we have to define three angular momentum operators: • These operators work out to • For small rotations, can show • For large rotations, this can then be generalized to • Later, we will realize this must be modified when you include spin • In more than 3 D, it is more complicated

6 G. Solving Continuous Symmetry Problems Continuous Translations • Consider the following potential in 3 D: • Note that V does not depend on Z • H must commute with the generator Pz • We can diagonalize Pz and H simultaneously

Reducing a 3 D Problem to a 2 D Problem • This helps you find wave functions: • The “proportionality constant” may depend on x and y: • Substitute into Schrödinger’s equation: • We have reduced a 3 D problem to a 2 D problem

Multiple Translation Symmetries • What if we have more than one translation? • Most extreme case: Three translation symmetries • We then find our functions: • Substitute into Schrödinger’s equation:

Lz in Polar Coordinates • Consider a 2 D potential that is rotationally symmetric • It follows that Hamiltonian invariant under rotations • The Hamiltonian commutes with Lz • We can choose our eigenstates to be eigenstates of Lz • It will be helpful to work in polar coordinates • Let’s try to write Lz in polar coordinates

Solving Problems with Rotational Symmetry • We write our wave function in polar coordinates • We now use the Lz equation to help find the wave function • Recall, the angle is 2 ambiguous • You can then substitute this into the Schrödinger equation • But you have to write the 2 D Laplacian in polar coordinates

Sample Problem: Bessel Functions A particle of mass in 2 D is in the circular infinite square well. Find the eigenstates and eigenvalues. • The problem is rotationally symmetric so • Write out Schrödinger’s equation – In allowed region, no potential • We now define a new variable x that is rescaled • This equation is called Bessel’s equations

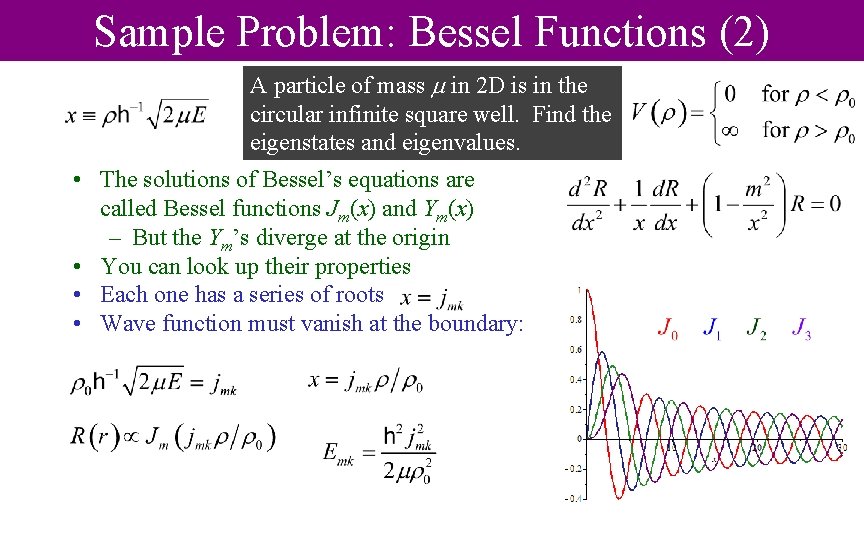
Sample Problem: Bessel Functions (2) A particle of mass in 2 D is in the circular infinite square well. Find the eigenstates and eigenvalues. • The solutions of Bessel’s equations are called Bessel functions Jm(x) and Ym(x) – But the Ym’s diverge at the origin • You can look up their properties • Each one has a series of roots • Wave function must vanish at the boundary:

Problems with 2 or 3 rotation symmetries? • Recall • Suppose H commutes with two rotation generators in 3 D • It must automatically commute with the third: • Can we diagonalize all three operators, along with the Hamiltonian? • No: all the operators must commute with each other