6 Sampling Distributions Lesson 6 3 The Sampling

6 Sampling Distributions Lesson 6. 3 The Sampling Distribution of a Sample Count (The Normal Approximation to the Binomial) Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

The Sampling Distribution of a Sample Count Learning Targets After this lesson, you should be able to: ü Calculate the mean and the standard deviation of the sampling distribution of a sample count and interpret the standard deviation. ü Determine if the sampling distribution of a sample count is approximately normal. ü If appropriate, use the normal approximation to the binomial distribution to calculate probabilities involving a sample count. Statistics and Probability with Applications, 3 rd Edition 2

The Sampling Distribution of a Sample Count In many cases, we are interested in the number of successes X in a random sample from some population. To do probability calculations involving X, we want an understanding of the sampling distribution of the sample count X. Sampling Distribution of the Sample Count X The sampling distribution of the sample count X describes the distribution of values taken by the sample count X in all possible samples of the same size from the same population. The sampling distribution of X is closely related to the binomial distributions that you learned about in Lessons 5. 3 and 5. 4. Statistics and Probability with Applications, 3 rd Edition 3

The Sampling Distribution of a Sample Count Because the sampling distribution of a sample count X is approximately binomial when the sample is a small fraction of the population, we can use the formulas from Lesson 5. 4 to calculate the mean and standard deviation of X. How to Calculate µX and σX for a Binomial Distribution Suppose X is the number of successes in a random sample of size n from a large population with proportion of successes p. Then: • The mean of the sampling distribution of X is • The standard deviation of the sampling distribution of X is Statistics and Probability with Applications, 3 rd Edition 4

Rubber ducky, are you the one? Mean and SD of the sampling distribution of X • Statistics and Probability with Applications, 3 rd Edition 5

The Sampling Distribution of a Sample Count The shape of a binomial distribution can be skewed to the right, skewed to the left, or roughly symmetric. The shape of the sampling distribution of X will be approximately normal when the sample size is large enough. “Large enough” depends on the value of p. The farther p is from 0. 5, the larger the sample size needs to be. The Large Counts Condition Suppose X is the number of successes in a random sample of size n from a population with proportion of successes p. The Large Counts condition says that the distribution of X will be approximately normal when np ≥ 10 and n(1 - p) ≥ 10 When the Large Counts condition is met, we can use a normal distribution to calculate probabilities involving X = the number of successes in a random sample of size n. Statistics and Probability with Applications, 3 rd Edition 6

Spend or save? Shape of the sampling distribution of a sample count • Statistics and Probability with Applications, 3 rd Edition 7

The most romantic dinner? Probabilities involving X • Statistics and Probability with Applications, 3 rd Edition 8
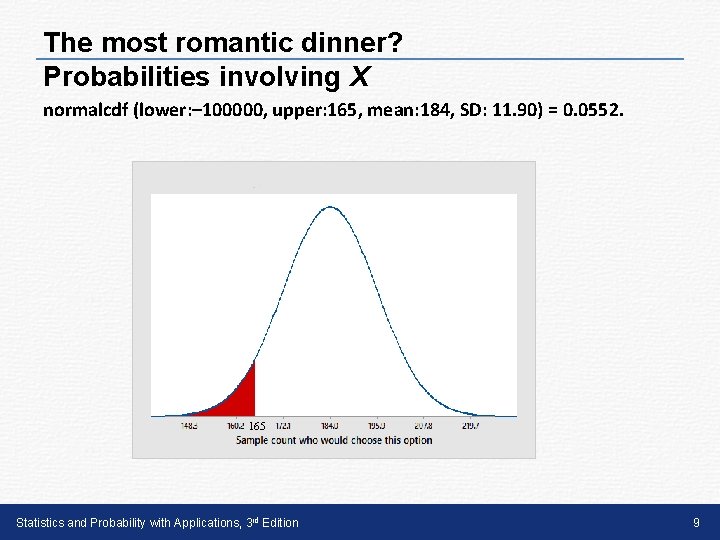
The most romantic dinner? Probabilities involving X normalcdf (lower: – 100000, upper: 165, mean: 184, SD: 11. 90) = 0. 0552. 165 Statistics and Probability with Applications, 3 rd Edition 9

LESSON APP 6. 3 How can we check for bias in a survey? One way of checking the effect of undercoverage, nonresponse, and other sources of bias in a sample survey is to compare the sample with known facts about the population. About 12% of American adults identify themselves as black. Suppose we take an SRS of 1500 American adults and let X be the number of blacks in the sample. 1. Calculate the mean and standard deviation of the sampling distribution of X. Interpret the standard deviation. 2. Justify that the sampling distribution of X is approximately normal. Statistics and Probability with Applications, 3 rd Edition 10
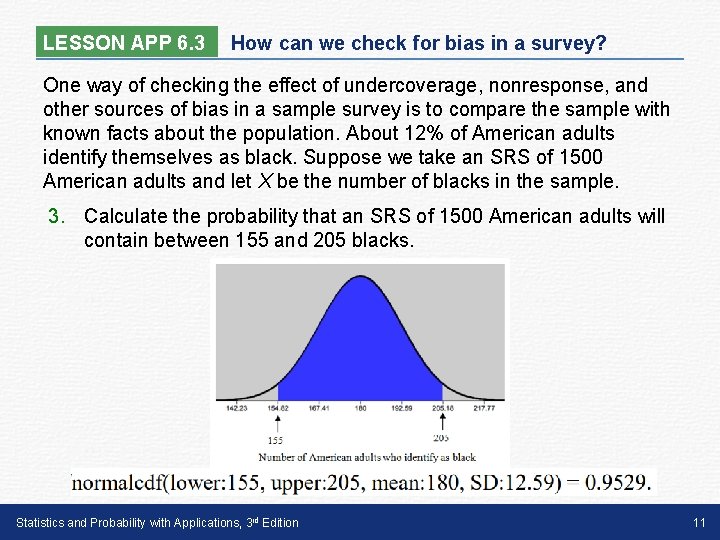
LESSON APP 6. 3 How can we check for bias in a survey? One way of checking the effect of undercoverage, nonresponse, and other sources of bias in a sample survey is to compare the sample with known facts about the population. About 12% of American adults identify themselves as black. Suppose we take an SRS of 1500 American adults and let X be the number of blacks in the sample. 3. Calculate the probability that an SRS of 1500 American adults will contain between 155 and 205 blacks. Statistics and Probability with Applications, 3 rd Edition 11

LESSON APP 6. 3 How can we check for bias in a survey? One way of checking the effect of undercoverage, nonresponse, and other sources of bias in a sample survey is to compare the sample with known facts about the population. About 12% of American adults identify themselves as black. Suppose we take an SRS of 1500 American adults and let X be the number of blacks in the sample. 4. Explain how a polling organization could use the results from the previous question to check for undercoverage and other sources of bias. Statistics and Probability with Applications, 3 rd Edition 12

The Sampling Distribution of a Sample Count Learning Targets After this lesson, you should be able to: ü Calculate the mean and the standard deviation of the sampling distribution of a sample count and interpret the standard deviation. ü Determine if the sampling distribution of a sample count is approximately normal. ü If appropriate, use the normal approximation to the binomial distribution to calculate probabilities involving a sample count. Statistics and Probability with Applications, 3 rd Edition 13
- Slides: 13