6 Sampling Distributions Lesson 6 1 What is

6 Sampling Distributions Lesson 6. 1 What is a Sampling Distribution? Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

What is a Sampling Distribution? Learning Targets After this lesson, you should be able to: ü Distinguish between a parameter and a statistic. ü Create a sampling distribution using all possible samples from a small population. ü Use the sampling distribution of a statistic to evaluate a claim about a parameter. Statistics and Probability with Applications, 3 rd Edition 2

What is a Sampling Distribution? As we begin to use sample data to draw conclusions about a wider population, we must be clear about whether a number describes a sample or a population. Statistic, Parameter A statistic is a number that describes some characteristic of a sample. A parameter is a number that describes some characteristic of the population. Remember s and p: statistics come from samples and parameters come from populations Statistics and Probability with Applications, 3 rd Edition 3

Pictures of co-workers? Parameters and statistics • Statistics and Probability with Applications, 3 rd Edition 4

Pictures of co-workers? Parameters and statistics • Statistics and Probability with Applications, 3 rd Edition 5

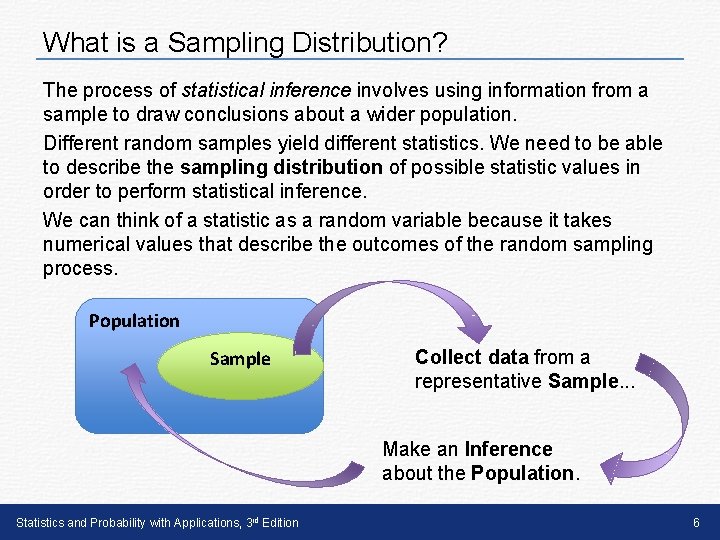
What is a Sampling Distribution? The process of statistical inference involves using information from a sample to draw conclusions about a wider population. Different random samples yield different statistics. We need to be able to describe the sampling distribution of possible statistic values in order to perform statistical inference. We can think of a statistic as a random variable because it takes numerical values that describe the outcomes of the random sampling process. Population Sample Collect data from a representative Sample. . . Make an Inference about the Population. Statistics and Probability with Applications, 3 rd Edition 6

What is a Sampling Distribution? Sampling Distribution The sampling distribution of a statistic is the distribution of values taken by the statistic in all possible samples of the same size from the same population. Remember that a distribution describes the possible values of a variable and how often these values occur. The easiest way to picture a distribution is with a graph, such as a dotplot or histogram. Every statistic has its own sampling distribution. Statistics and Probability with Applications, 3 rd Edition 7

Disproportionate males? Sampling distributions PROBLEM: There are six employees in a small company, Atsuko, Bernadette, Carlos, Dandre, Easton, and Freddie. Atsuko and Bernadette are female and the others are male. List all 15 possible SRSs of size n = 4, calculate the proportion of males for each sample, and display the sampling distribution of the sample proportions on a dotplot. Statistics and Probability with Applications, 3 rd Edition 8

What is a Sampling Distribution? Caution: Be specific when you use the word “distribution. ” There can be multiple distributions for a given setting. See the example on p. 402. 1. The distribution of height in the population (the four heights): 2. The distribution of heights in a particular sample (two of the heights): 3. The sampling distribution of the sample range for all possible samples (the six sample ranges): Statistics and Probability with Applications, 3 rd Edition 9

What’s in the box? Evaluating a claim • Statistics and Probability with Applications, 3 rd Edition 10

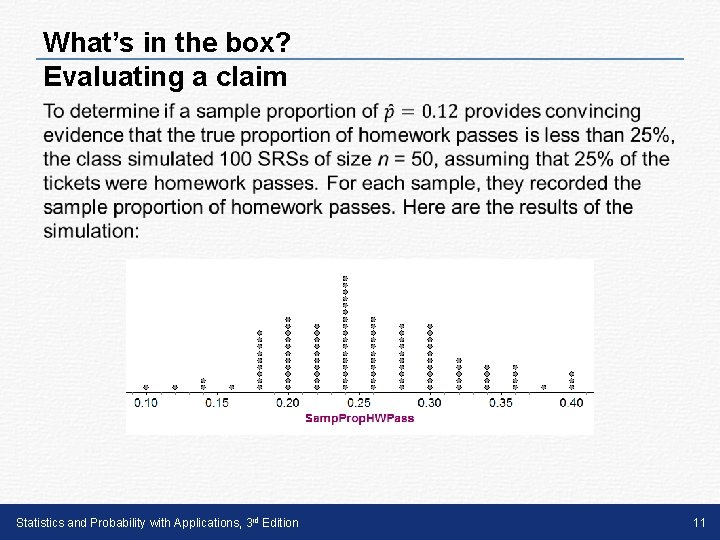
What’s in the box? Evaluating a claim • Statistics and Probability with Applications, 3 rd Edition 11

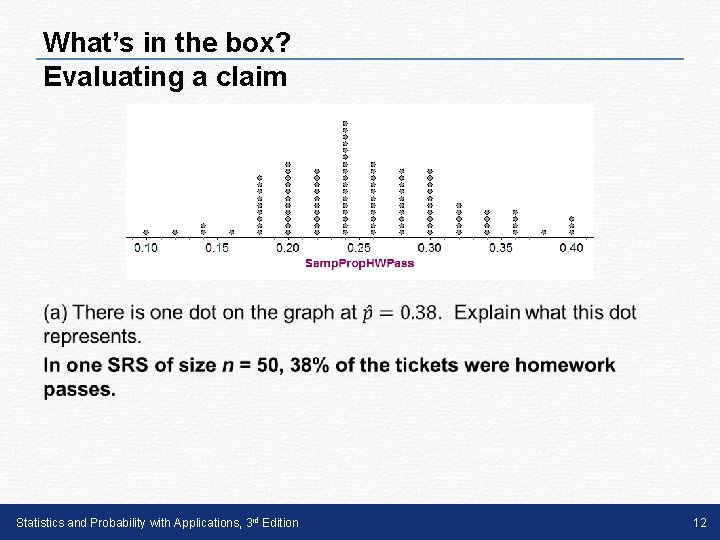
What’s in the box? Evaluating a claim • Statistics and Probability with Applications, 3 rd Edition 12

What’s in the box? Evaluating a claim (b) Would it be unusual to get a sample proportion of 0. 12 or less in a sample of size 50 when p = 0. 25? Explain. Yes. In the 100 trials of the simulation, only 2 of the SRSs included 12% or fewer homework passes. Statistics and Probability with Applications, 3 rd Edition 13

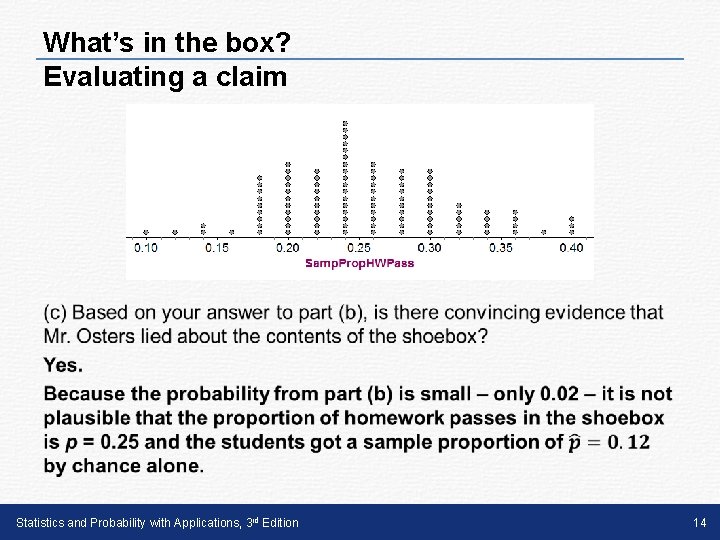
What’s in the box? Evaluating a claim • Statistics and Probability with Applications, 3 rd Edition 14

LESSON APP 6. 1 How cold is it inside the cabin? During the winter months, outside temperatures at the Starneses' cabin in Colorado can stay well below freezing (32°F, or 0°C) for weeks at a time. To prevent the pipes from freezing, Mrs. Starnes sets thermostat at 50°F. The manufacturer claims that thermostat allows variation in home temperature that follows a normal distribution with σ = 3°F. To test this claim, Mrs. Starnes programs her digital thermostat to take an SRS of n =10 readings during a 24 -hour period. The standard deviation of the results is sx = 5°F. 1. Identify the population, the parameter, the sample, and the statistic in this context. Statistics and Probability with Applications, 3 rd Edition 15

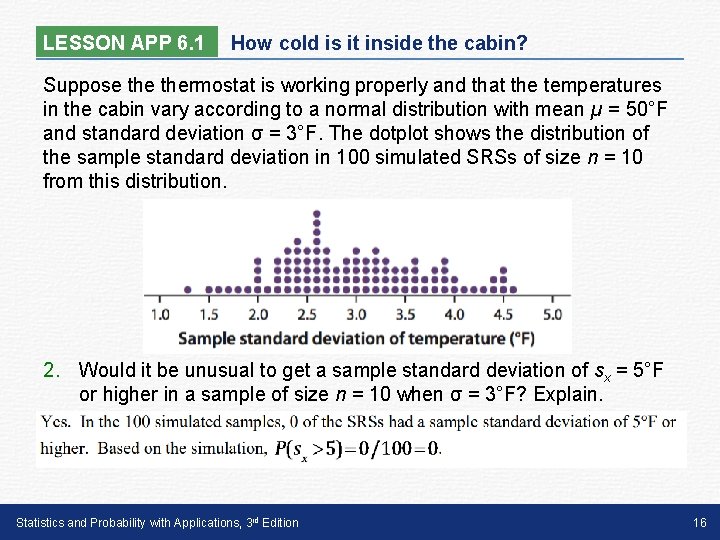
LESSON APP 6. 1 How cold is it inside the cabin? Suppose thermostat is working properly and that the temperatures in the cabin vary according to a normal distribution with mean µ = 50°F and standard deviation σ = 3°F. The dotplot shows the distribution of the sample standard deviation in 100 simulated SRSs of size n = 10 from this distribution. 2. Would it be unusual to get a sample standard deviation of sx = 5°F or higher in a sample of size n = 10 when σ = 3°F? Explain. Statistics and Probability with Applications, 3 rd Edition 16

LESSON APP 6. 1 How cold is it inside the cabin? Suppose thermostat is working properly and that the temperatures in the cabin vary according to a normal distribution with mean µ = 50°F and standard deviation σ = 3°F. The dotplot shows the distribution of the sample standard deviation in 100 simulated SRSs of size n = 10 from this distribution. 3. Based on your answer to Question 2, is there convincing evidence that thermometer is more variable than the manufacturer claims? Explain. Statistics and Probability with Applications, 3 rd Edition 17

What is a Sampling Distribution? Learning Targets After this lesson, you should be able to: ü Distinguish between a parameter and a statistic. ü Create a sampling distribution using all possible samples from a small population. ü Use the sampling distribution of a statistic to evaluate a claim about a parameter. Statistics and Probability with Applications, 3 rd Edition 18