6 s1 Linear Programming Operations Management OPERATIONS RESEARCH

6 s-1 Linear Programming Operations Management OPERATIONS RESEARCH William J. Stevenson 8 th edition

6 s-2 Linear Programming MASALAH PENUGASAN (ASSIGMENT PROBLEM) Masalah yang berhubungan dengan penugasan optimal dari bermacam-macam sumber yang produktif atau personalia yang mempunyai tingkat efisiensi yang berbeda-beda untuk tugas-tugas yang berbeda-beda pula

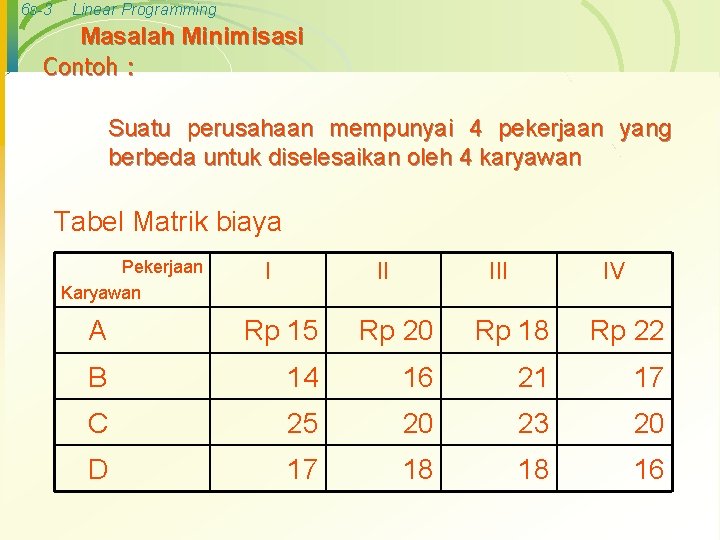
6 s-3 Linear Programming Masalah Minimisasi Contoh : Suatu perusahaan mempunyai 4 pekerjaan yang berbeda untuk diselesaikan oleh 4 karyawan Tabel Matrik biaya Pekerjaan Karyawan I II IV A Rp 15 Rp 20 Rp 18 Rp 22 B 14 16 21 17 C 25 20 23 20 D 17 18 18 16

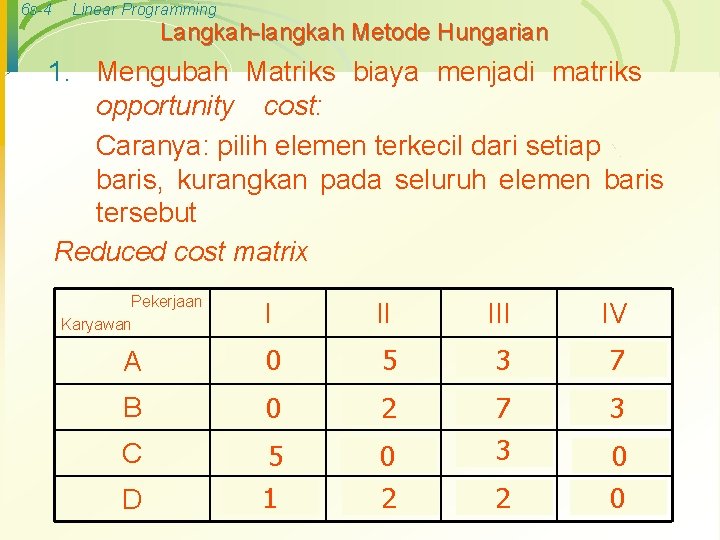
6 s-4 Linear Programming Langkah-langkah Metode Hungarian 1. Mengubah Matriks biaya menjadi matriks opportunity cost: Caranya: pilih elemen terkecil dari setiap baris, kurangkan pada seluruh elemen baris tersebut Reduced cost matrix Pekerjaan Karyawan I II IV A Rp 0 15 Rp 5 20 3 18 Rp 7 22 Rp B 0 14 2 16 3 17 C 5 25 1 17 0 20 2 18 7 21 3 23 D 2 18 0 20 0 16

6 s-5 Linear Programming 2. Reduced-cost matrix terus dikurangi untuk mendapatkan totalopportunity-cost matrix. pilih elemen terkecil dari setiap kolom pada RCM yang tidak mempunyai nilai nol, kurangkan pada seluruh elemen dalam kolom tersebut. Reduced cost matrix Total opportunity cost matrix Pekerjaan Karyawan I II IV A 0 5 31 7 B 0 2 3 C 5 0 75 31 D 1 2 20 0 0

6 s-6 Linear Programming 3. Melakukan test optimalisasi dengan menarik sejumlah minimum garis horisontal dan/atau vertikal untuk meliput seluruh elemen bernilai nol Penugasan optimal adalah feasible jika : jumlah garis = min(jumlah baris atau kolom) Test of optimality Pekerjaan I Karyawan II IV A 0 5 1 7 B 0 2 5 3 C 5 0 1 0 D 1 2 0 0

6 s-7 Linear Programming 4. Untuk merevisi total-opportunity matrix, pilih elemen terkecil yang belum terliput garis (1) untuk mengurangi seluruh elemen yang belum terliput Tambahkan jumlah yang sama pada seluruh elemen yang mempunyai dua garis yang saling bersilangan Ulangi langkah 3 Revised matrix dan Test of optimality Pekerjaan I II III Karyawan A 0 B C 0 6 5 D 2 1 IV 45 12 10 4 5 7 6 2 3 0 1 0 2 0 0

6 s-8 Linear Programming Melakukan test optimalisasi dengan menarik sejumlah minimum garis horisontal dan/atau vertikal untuk meliput seluruh elemen bernilai nol Karena jumlah garis = min( jumlah baris atau kolom) maka matrik penugasan optimal telah tercapai Revised matrix dan Test of optimality Pekerjaan Karyawan I II IV A 0 B 10 4 5 7 6 2 3 C 0 6 5 45 12 0 1 0 D 2 1 2 0 0

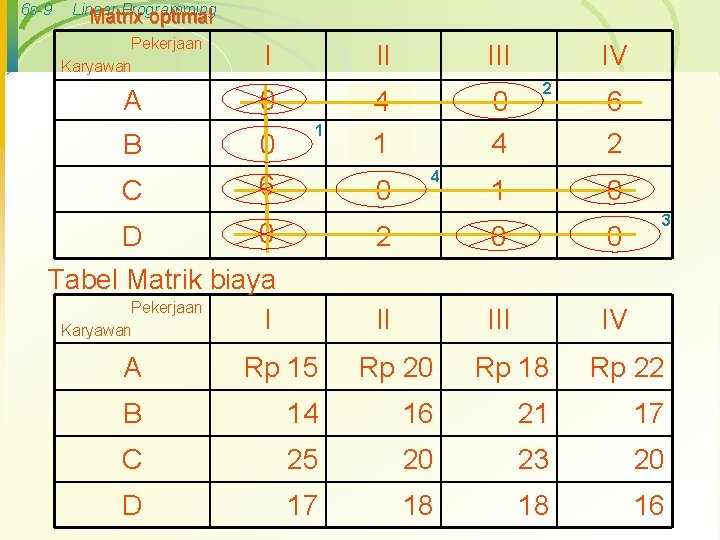
6 s-9 Linear Programming Matrix optimal Pekerjaan Karyawan A B C I II 0 0 6 5 1 III 45 12 0 10 4 5 4 IV 2 1 7 6 2 3 0 0 1 2 0 0 Tabel Matrik biaya Pekerjaan I Karyawan II IV D 3 A Rp 15 Rp 20 Rp 18 Rp 22 B 14 16 21 17 C 25 20 23 20 D 17 18 18 16

6 s-10 Linear Programming Skedul penugasan optimal Skedul penugasan A - III Rp 18 B -I 14 C - II 20 D - IV 16 Rp 68 Karyawan B ditugaskan untuk pekerjaan satu karena baris B hanya mempunyai satu nilai nol

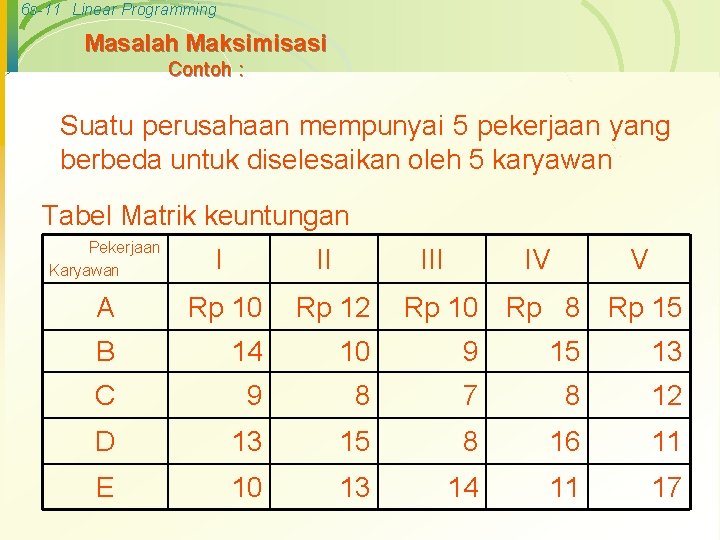
6 s-11 Linear Programming Masalah Maksimisasi Contoh : Suatu perusahaan mempunyai 5 pekerjaan yang berbeda untuk diselesaikan oleh 5 karyawan Tabel Matrik keuntungan Pekerjaan Karyawan I II IV V A Rp 10 Rp 12 Rp 10 Rp 8 Rp 15 B 14 10 9 15 13 C 9 8 7 8 12 D 13 15 8 16 11 E 10 13 14 11 17

6 s-12 Linear Programming Langkah-langkah Metode Hungarian 1. Mengubah Matriks biaya menjadi matriks opportunity-loss: Caranya: pilih elemen terbesar dari setiap baris, kurangkan pada seluruh elemen baris tersebut Opportunity-loss matrix Pekerjaan Karyawan I II IV V B Rp 5 10 1 14 Rp 3 12 5 10 C 3 9 4 8 5 7 4 8 0 12 D 3 13 7 10 1 15 4 13 8 8 3 14 0 16 6 11 5 11 0 17 A E Rp 5 10 Rp 7 8 Rp 0 15 6 9 0 15 2 13

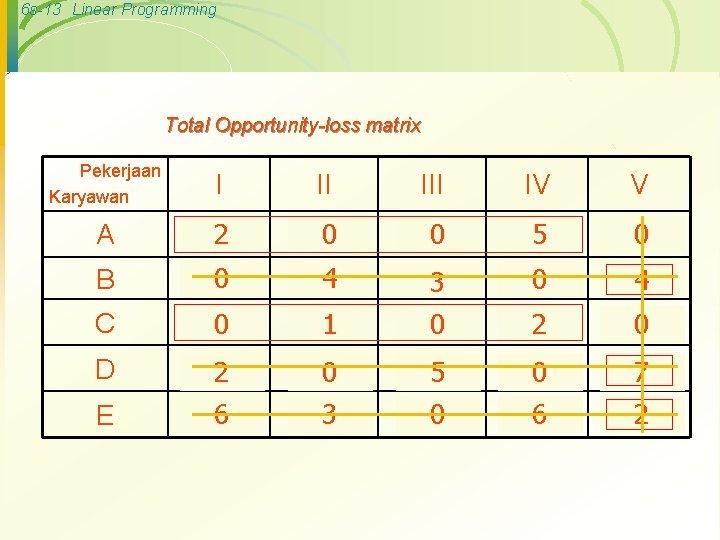
6 s-13 Linear Programming Total Opportunity-loss matrix Pekerjaan Karyawan I II A 5 10 2 Rp 4 3 0 12 Rp 2 B 0 1 14 4 5 10 C 2 0 3 9 D 3 13 2 7 10 6 E III IV V 5 10 Rp 7 0 5 8 Rp 0 15 Rp 2 0 15 2 4 13 4 3 1 8 6 9 3 2 0 5 7 4 2 8 0 12 1 15 0 4 13 3 8 8 5 3 14 0 0 16 6 11 5 7 11 0 2 17

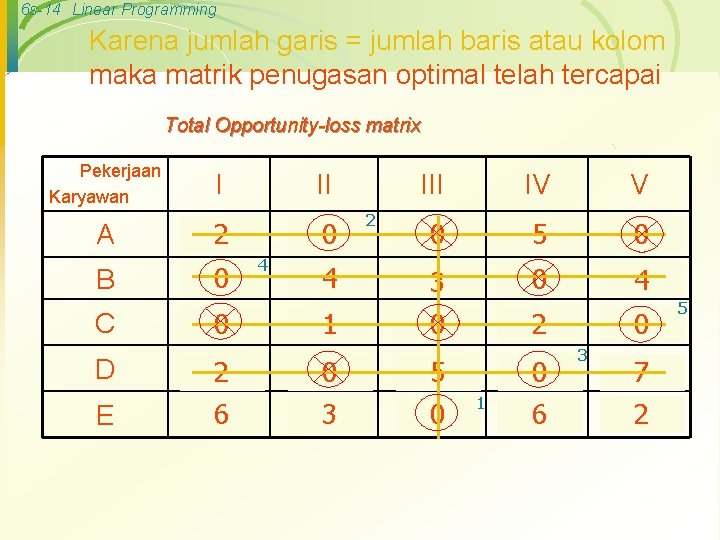
6 s-14 Linear Programming Karena jumlah garis = jumlah baris atau kolom maka matrik penugasan optimal telah tercapai Total Opportunity-loss matrix Pekerjaan Karyawan A B C D E I II 5 4 10 Rp 2 4 0 14 1 0 3 2 9 3 2 13 6 10 7 III 2 3 0 12 Rp 2 4 5 10 4 3 1 8 1 15 0 3 4 13 IV V 5 0 10 Rp 7 5 8 Rp 0 15 Rp 2 6 9 3 5 2 0 7 8 8 5 1 0 3 14 0 15 4 2 8 3 0 16 6 11 2 4 13 5 0 12 5 7 11 2 17 0

6 s-15 Linear Programming SEKIAN