6 s1 Linear Programming Operations Management OPERATIONS RESEARCH

6 s-1 Linear Programming Operations Management OPERATIONS RESEARCH LINIER PROGRAMMING William J. Stevenson Rosihan Asmara http: //lecture. brawijaya. ac. id/rosihan http: //rosihan. com 8 th edition

6 s-2 Linear Programming LINEAR PROGRAMMING suatu model umum yang dapat digunakan dalam pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal. Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau menentukan tingkat setiap kegiatan yang akan dilakukannya, dimana masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas

6 s-3 Linear Programming Dalam model LP dikenal 2 (dua) macam “fungsi”, 1. 2. Fungsi tujuan adalah fungsi yang menggambarkan tujuan sasaran di dalam permasalahan LP yang berkaitan dengan pengaturan secara optimal sumberdaya, untuk memperoleh keuntungan maksimal atau biaya minimal. Pada umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z. Fungsi batasan merupakan bentuk penyajian secara matematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.

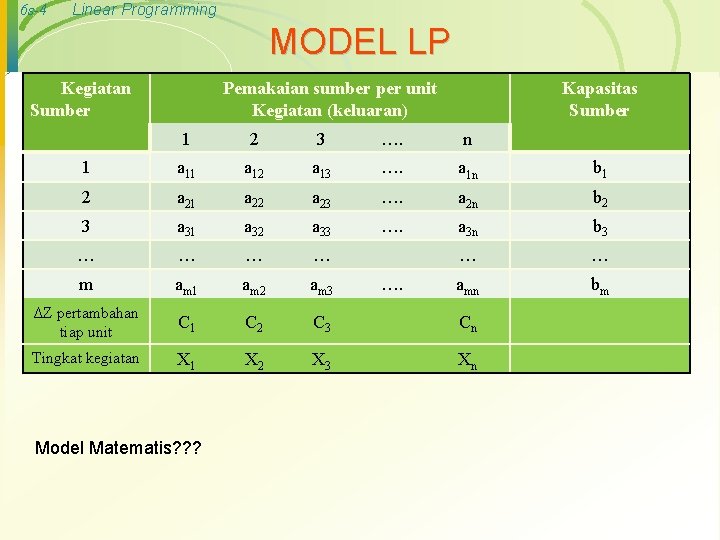
6 s-4 Linear Programming MODEL LP Kegiatan Sumber Pemakaian sumber per unit Kegiatan (keluaran) Kapasitas Sumber 1 2 3 …. n 1 a 12 a 13 …. a 1 n b 1 2 a 21 a 22 a 23 …. a 2 n b 2 3 a 31 a 32 a 33 …. a 3 n b 3 … … … m am 1 am 2 am 3 amn bm ΔZ pertambahan tiap unit C 1 C 2 C 3 Cn Tingkat kegiatan X 1 X 2 X 3 Xn Model Matematis? ? ? ….

6 s-5 Linear Programming Model Matematis · Fungsi tujuan: · · Maksimumkan Z = C 1 X 1+ C 2 X 2+ C 3 X 3+ …. + Cn. Xn Batasan : 1. a 11 X 11+ a 12 X 2 + a 13 X 3 + …. + a 1 n. Xn 2. a 21 X 11+ a 22 X 2 + a 33 X 3 + …. + a 2 n. Xn ≤ b 1 …. . m. am 1 X 11+ am 2 X 2 + am 3 X 3 + …. + amn. Xn dan X 1 ≥ 0, X 2 ≥ 0, ………. Xn ≥ 0 ≤ bm

6 s-6 Linear Programming Asumsi-asumsi Dasar Linear Programming 1. Proportionality naik turunnya nilai Z dan penggunaan sumber atau fasilitas yang tersedia akan berubah secara sebanding (proportional) dengan perubahan tingkat kegiatan 2. Additivity nilai tujuan tiap kegiatan tidak saling mempengaruhi, atau dalam LP dianggap bahwa kenaikan dari nilai tujuan (Z) yang diakibatkan oleh kenaikan suatu kegiatan dapat ditambahkan tanpa mempengaruhi bagian nilai Z yang diperoleh dari kegiatan lain

6 s-7 Linear Programming Asumsi-asumsi Dasar Linear Programming 3. Divisibility keluaran (output) yang dihasilkan oleh setiap kegiatan dapat berupa bilangan pecahan. Demikian pula dengan nilai Z yang dihasilkan 4. Deterministic (Certainty) Asumsi ini menyatakan bahwa semua parameter yang terdapat dalam model LP (aij, bi Cj) dapat diperkirakan dengan pasti, meskipun jarang dengan tepat

6 s-8 Linear Programming LINEAR PROGRAMMING DENGAN METODE GRAFIK Contoh Perusahaan sepatu membuat 2 macam sepatu. Yang pertama merek I 1, dgn sol karet, dan merek I 2 dgn sol kulit. Diperlukan 3 macam mesin. Mesin 1 membuat sol karet, mesin 2 membuat sol kulit, dan mesin 3 membuat bagian atas sepatu dan melakukan assembling bagian atas dengan sol. Setiap lusin sepatu merek I 1 mula-mula dikerjakan di mesin 1 selama 2 jam, kemudian tanpa melalui mesin 2 terus dikerjakan di mesin 3 selama 6 jam. Sedang untuk sepatu merek I 2 tidak diproses di mesin 1, tetapi pertama kali dikerjakan di mesin 2 selama 3 jam kemudian di mesin 3 selama 5 jam. Jam kerja maksimum setiap hari mesin 1 adalah 8 jam, mesin 2 adalah 15 jam, dan mesin 3 adalah 30 jam. Sumbangan terhadap laba setiap lusin sepatu merek I 1 = Rp 30. 000, 00 sedang merek I 2 = Rp 50. 000, 00. Masalahnya adalah menentukan berapa lusin sebaiknya sepatu merek I 1 dan merek I 2 yang dibuat agar bisa memaksimumkan laba.

6 s-9 Linear Programming Bentuk Tabel Merek Mesin 1 2 3 Sumbangan laba I 1 (X 1) 2 0 6 I 2 (X 2) 0 3 5 Kapasitas Maksimum 8 15 30

6 s-10 Linear Programming Bentuk Matematis Maksimumkan Z = 3 X 1 + 5 X 2 · Batasan (constrain) (1) 2 X 1 8 (2) 3 X 2 15 (3) 6 X 1 + 5 X 2 30 ·

6 s-11 Linear Programming Fungsi batasan pertama (2 X 1 8) X 2 2 X 1 = 8 2 X 1 8 dan X 1 0, X 2 0 0 4 X 1 Gambar di atas merupakan bagian yang memenuhi batasan-batasan: X 1 0, X 2 0 dan 2 X 1 8

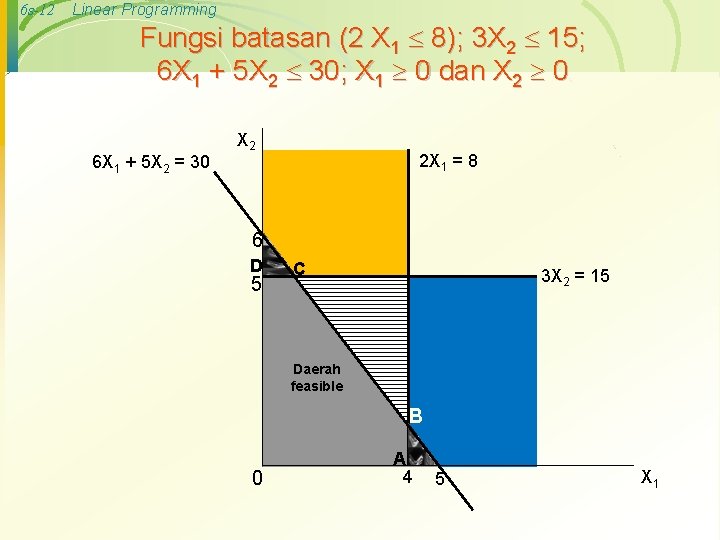
6 s-12 Linear Programming Fungsi batasan (2 X 1 8); 3 X 2 15; 6 X 1 + 5 X 2 30; X 1 0 dan X 2 0 6 X 1 + 5 X 2 = 30 X 2 2 X 1 = 8 6 D 5 C 3 X 2 = 15 Daerah feasible B 0 A 4 5 X 1

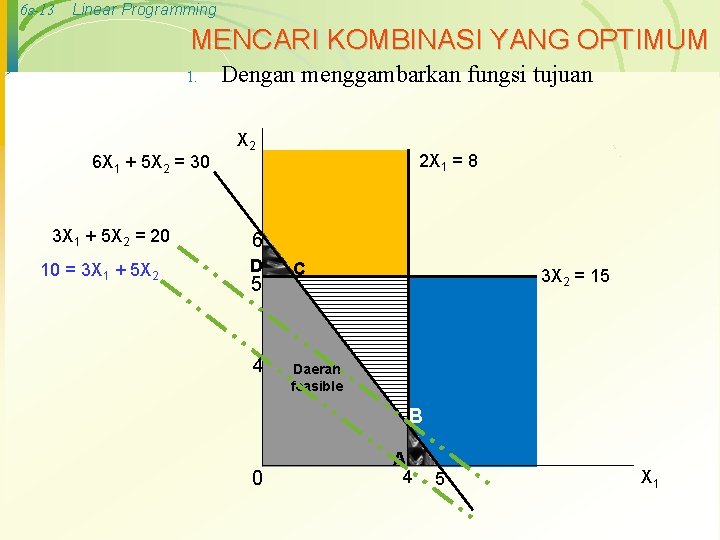
6 s-13 Linear Programming MENCARI KOMBINASI YANG OPTIMUM 1. 6 X 1 + 5 X 2 = 30 3 X 1 + 5 X 2 = 20 10 = 3 X 1 + 5 X 2 Dengan menggambarkan fungsi tujuan X 2 2 X 1 = 8 6 D 5 4 C 3 X 2 = 15 Daerah feasible B 0 A 4 5 X 1

6 s-14 Linear Programming MENCARI KOMBINASI YANG OPTIMUM 2. Dengan membandingkan nilai Z pada tiap-tiap alternatif Z = 3 X 1 + 5 X 2 6 X 1 + 5 X 2 = 30 X 2 2 X 1 = 8 Titik C: Titik D: Pada titik ini nilai X 2 = 5; X 1 = 0 Nilai Z = 3(0) + 5(5) = 25 X 2 = 5. Substitusikan batasan (3), maka 6 X 1 + 5(5) = 30. Jadi nilai X 1 = (30 – 25)/6 = 5/6. Nilai Z = 3(5/6) + 5(5) = 27, 5 6 D 5 Titik B: C 3 X 2 = 15 Titik A: Daerah feasible X 1 = 4. Substitusikan batasan (3), maka 6(4) + 5 X 2 = 30. Jadi nilai X 2 = (30 – 24)/5 = 6/5. Nilai Z = 3(4) + 5(6/5) =18 Pada titik ini nilai X 1 = 4; X 2 = 0 Nilai Z = 3(4) + 0 = 12 B 0 A 4 5 X 1

6 s-15 Linear Programming Fungsi batasan bertanda “lebih besar atau sama dengan ( ) Contoh : Batasan ketiga (6 X 1 + 5 X 2 30) diubah ketidaksamaannya menjadi 6 X 1 + 5 X 2 30 X 2 2 X 2 = 8 6 X 1 + 5 X 2 = 30 6 5 3 X 2 = 15 B C Daerah feasible A 0 4 5 X 1

6 s-16 Linear Programming Fungsi batasan bertanda “sama dengan” ( = ) X 2 2 X 2 = 8 6 X 1 + 5 X 2 = 30 6 C B 3 X 2 = 15 4 2 A 0 4 5 X 1