6 Reliability Modeling Reliable System Design 2010 by

6. Reliability Modeling Reliable System Design 2010 by: Amir M. Rahmani

Concepts in Probability l Let X denote the lifetime for a component. F (t) = P ( X ≤ t ) Distribution function R (t) = 1 – F (t) = P (X > t ) Reliability function f (t ) = d F (t )/d t Probability density function matlab 1. ir

The exponential distribution F (t) = 1 -e -λt R (t) = e -λt f (t) = λe -λt l Distribution function Reliability function Probability density function λ is the failure rate for the component and t is the time matlab 1. ir

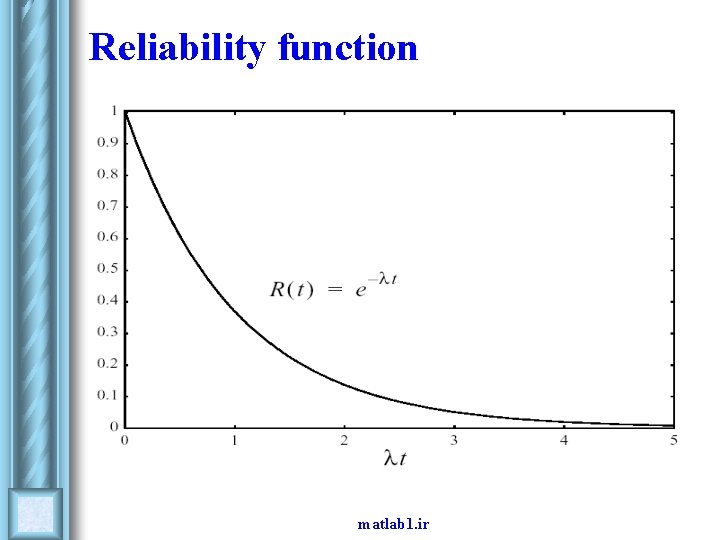
Reliability function matlab 1. ir

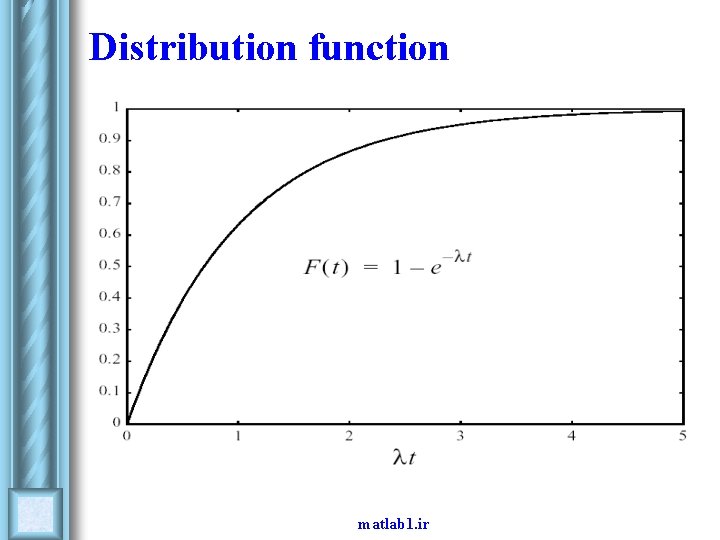
Distribution function matlab 1. ir

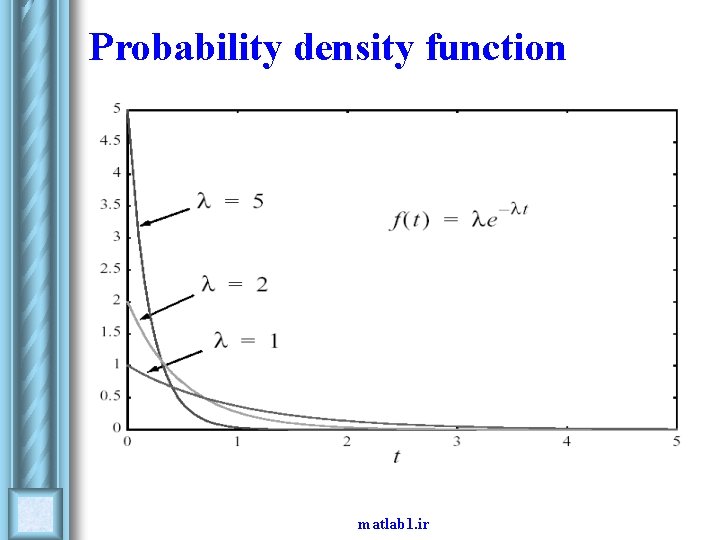
Probability density function matlab 1. ir

Failure rate function The exponential distribution has a constant failure rate: f (t)/R(t)= λe -λt /e -λt = λ l l Failure rate: • l - Fraction of “units_failing/(Total_unit× time)” Ex: 1000 units, 3 failed in 2 hours - Failure rate = 3/(1000× 2) = 1. 5× 10 -3 failure per hour matlab 1. ir •

Mean Time To Failure (MTTF) l Expected time to failure = - Corresponds to inverse of failure rate l Proof: Let X denote the lifetime for the component matlab 1. ir

MTTF for the exponential distribution , matlab 1. ir

Example MTTF l l What is the probability that a component with an exponentially distributed lifetime will survive the expected lifetime? Only 37% of the components survive the expected lifetime. matlab 1. ir

Reliability Block Diagrams l l Series systems Parallel systems m-of-n systems Combinational systems matlab 1. ir

Series system with n components l The reliability of the series system is l Iff the component failures are independent. matlab 1. ir

Series system of components with exponentially distributed lifetimes l The failure rate of the series system is equal to the sum of the component failure rates. matlab 1. ir

MTTF for a series system l The failure rate for the series system is l MTTF is matlab 1. ir

Example 1 - Series system l The reliability of the system is: matlab 1. ir

Parallel system with n components l l The reliability of the parallel system is: where Fpar is the failure probability (distribution function) for the parallel system and Fi the failure probability for component i matlab 1. ir

Examples l The reliability for parallel systems consisting of 2 or 3 identical components matlab 1. ir

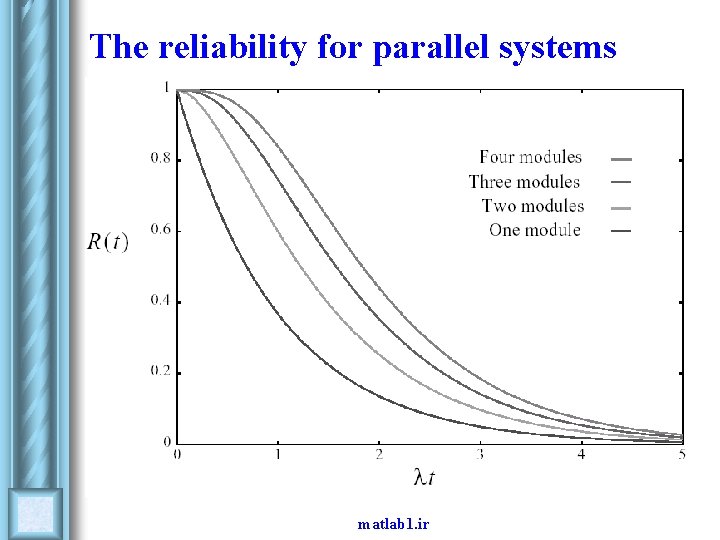
The reliability for parallel systems matlab 1. ir

MTTF for a parallel system with n components l Let X denote the lifetime of the system Make the substitution We then obtain: l Note that MTTF increases slowly with the number components in the system matlab 1. ir

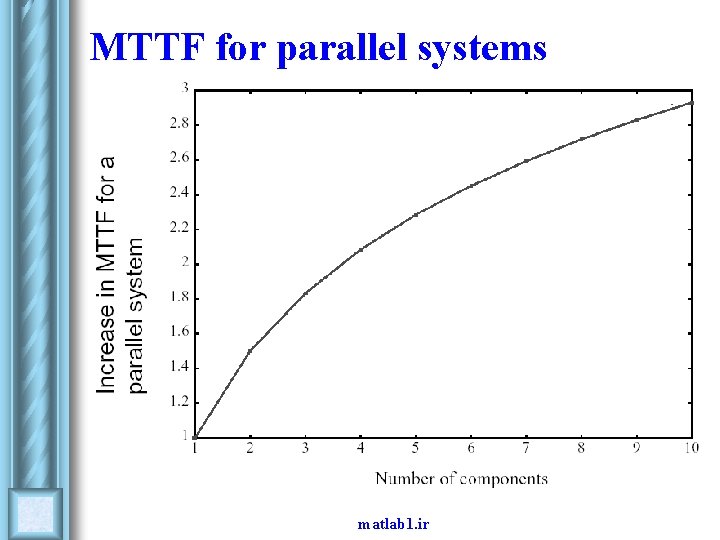
MTTF for parallel systems matlab 1. ir

Example - MTTF for parallel systems l What is the MTTF for a parallel system consisting of 4 components if the MTTF for one component is 1/λ? matlab 1. ir

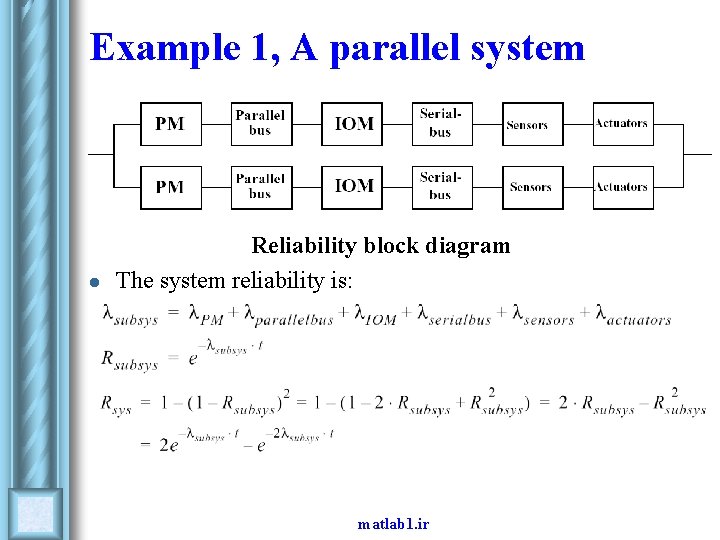
Example 1, A parallel system l Reliability block diagram The system reliability is: matlab 1. ir

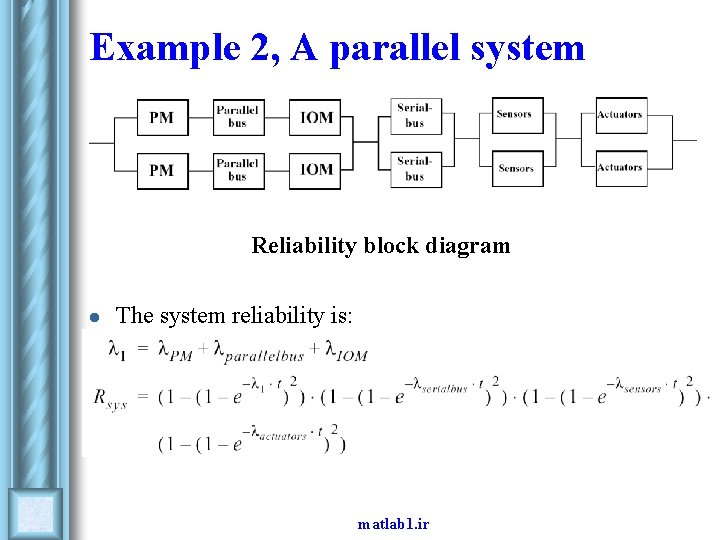
Example 2, A parallel system Reliability block diagram l The system reliability is: matlab 1. ir

Coverage l Failure detection: requires concurrent detection. • l Need redundancy. Switchover: • • good state loaded in U 2. Process restarted matlab 1. ir

Imperfect Coverage matlab 1. ir

Example m-of-n systems l l Obtain the reliability for a TMR system ( 2 -of-3 system). Let R denote the reliability for one module. RTMR = P (all modules are functioning) + P (two modules are functioning) = R 3 + 3 R 2 · (1 – R ) = 3 R 2 – 2 R 3 l If the lifetimes of the modules are exponentially distributed, we obtain: R = e-λt => RTMR =3 e-2λt – 2 e-3λt matlab 1. ir

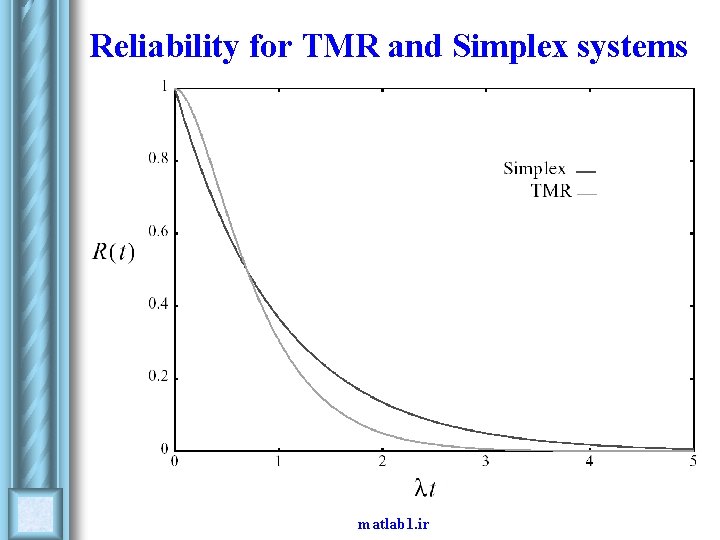
Reliability for TMR and Simplex systems matlab 1. ir

MTTF for a TMR-system l The MTTF for the TMR-system is only 5/6 of the MTTF for the simplex System! matlab 1. ir

m-of-n systems l In general, the reliability for an m-of-n system is: Example 1: 2 -of-3 system Example 2: 2 -of-4 system matlab 1. ir

Reliability Block Diagram l Series Parallel Graph • • • – a graph that is recursively composed of series and parallel structures. – therefore it can be “collapsed” by applying series and/or parallel reduction – Let Ci denote the condition that component i is operable • 1 = up, 0 = down • – Let S denote the condition that the system is operable • 1 = up, 0 = down • – S is a logic function of C’s matlab 1. ir

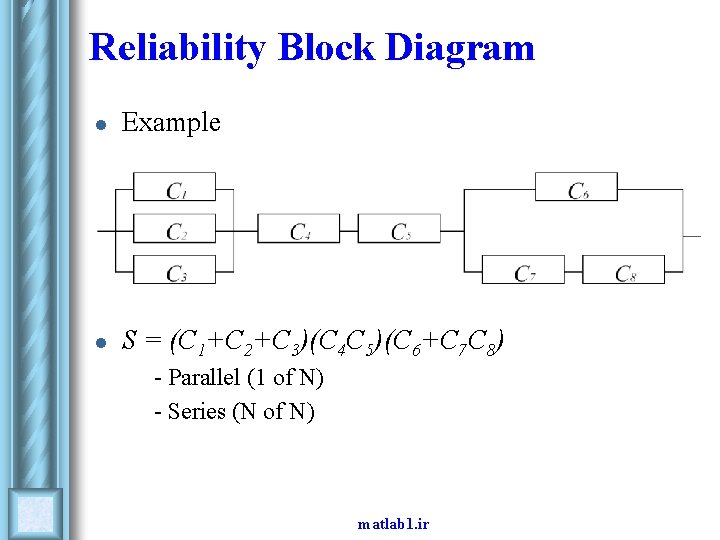
Reliability Block Diagram l Example l S = (C 1+C 2+C 3)(C 4 C 5)(C 6+C 7 C 8) • • - Parallel (1 of N) - Series (N of N) matlab 1. ir

Combinational systems l Example • Consider component or components that eliminating or considering the default mode of graph , could be changed into series or parallel combinations. matlab 1. ir

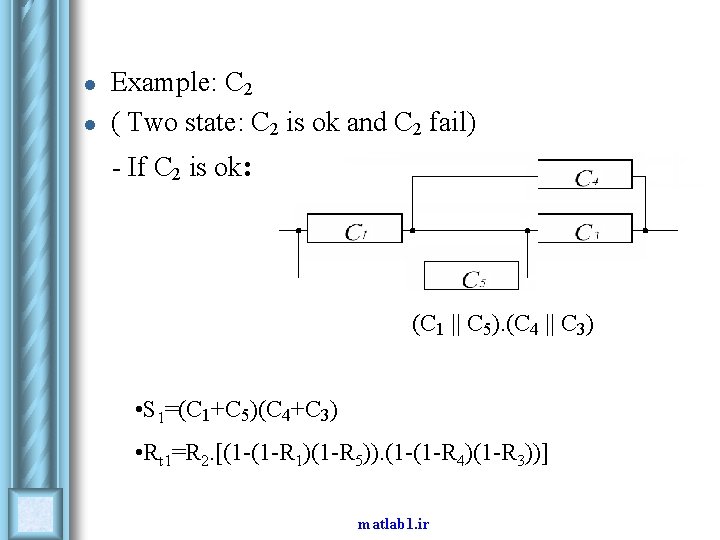
l l Example: C 2 ( Two state: C 2 is ok and C 2 fail) - If C 2 is ok: (C 1 || C 5). (C 4 || C 3) • S 1=(C 1+C 5)(C 4+C 3) • Rt 1=R 2. [(1 -(1 -R 1)(1 -R 5)). (1 -(1 -R 4)(1 -R 3))] matlab 1. ir

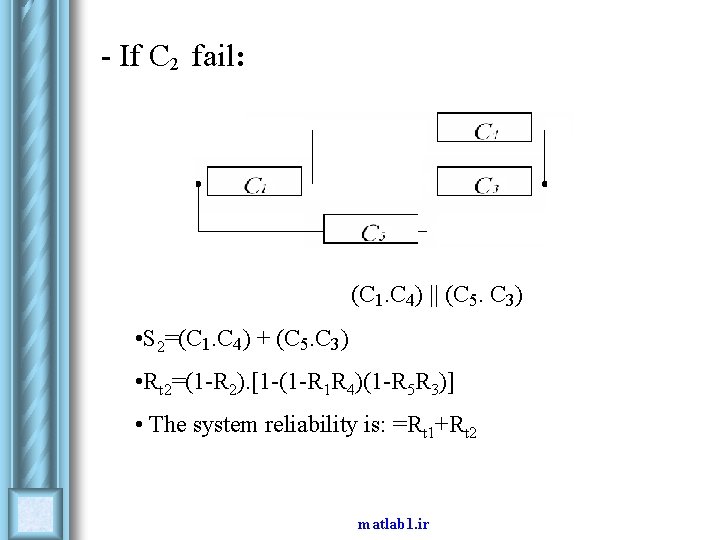
- If C 2 fail: (C 1. C 4) || (C 5. C 3) • S 2=(C 1. C 4) + (C 5. C 3) • Rt 2=(1 -R 2). [1 -(1 -R 1 R 4)(1 -R 5 R 3)] • The system reliability is: =Rt 1+Rt 2 matlab 1. ir

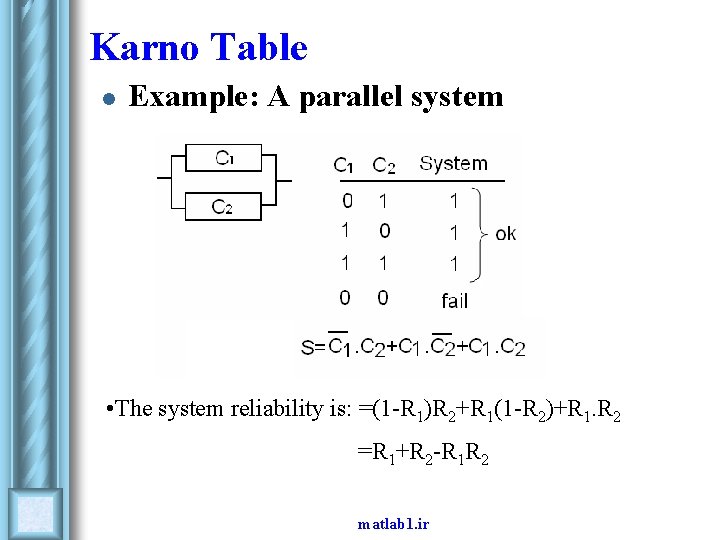
Karno Table l Example: A parallel system • The system reliability is: =(1 -R 1)R 2+R 1(1 -R 2)+R 1. R 2 =R 1+R 2 -R 1 R 2 matlab 1. ir