6 Reliability computations Objectives Learn how to compute

6. Reliability computations Objectives • Learn how to compute reliability of a component given the probability distributions on the stress, S , and the strength, Su. • Given the probability distributions of all input random variables, find the failure probability of a component • Learn how to estimate failure probability of components or systems using standard Monte-Carlo simulation and Monte -Carlo simulation with variance reduction techniques – Generate sample random numbers given their probability distributions – Estimate failure probability and quantify accuracy of the estimate 1

Finding probability of failure of component given the probability distributions of strength and stress • Definition: Performance function, z: – z>0 survival – z<0 failure – z=limit state Su z=0 z>0 z<0 (failure region) S 2
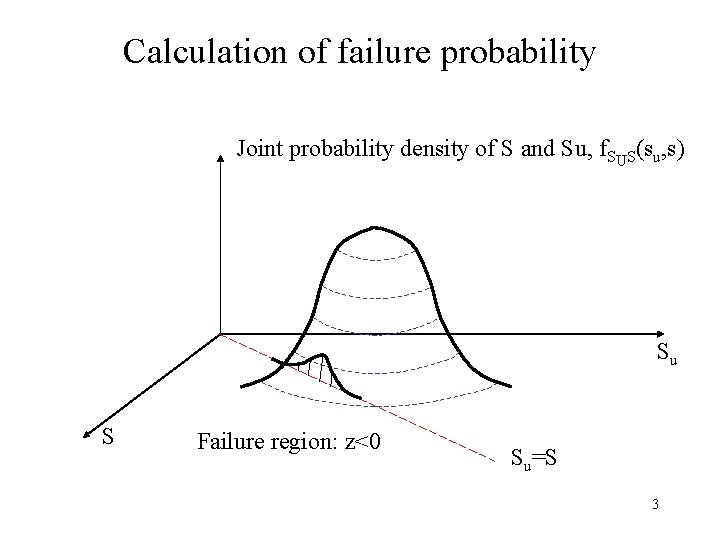
Calculation of failure probability Joint probability density of S and Su, f. SUS(su, s) Su S Failure region: z<0 Su=S 3

Calculation of failure probability 4
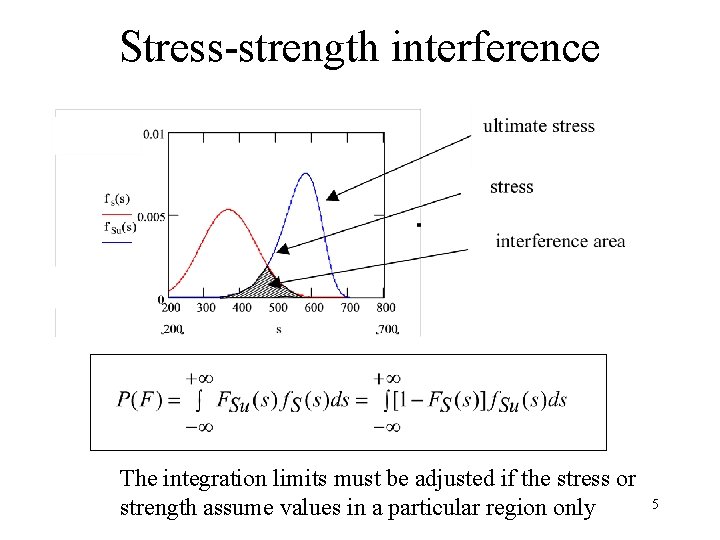
Stress-strength interference The integration limits must be adjusted if the stress or strength assume values in a particular region only 5
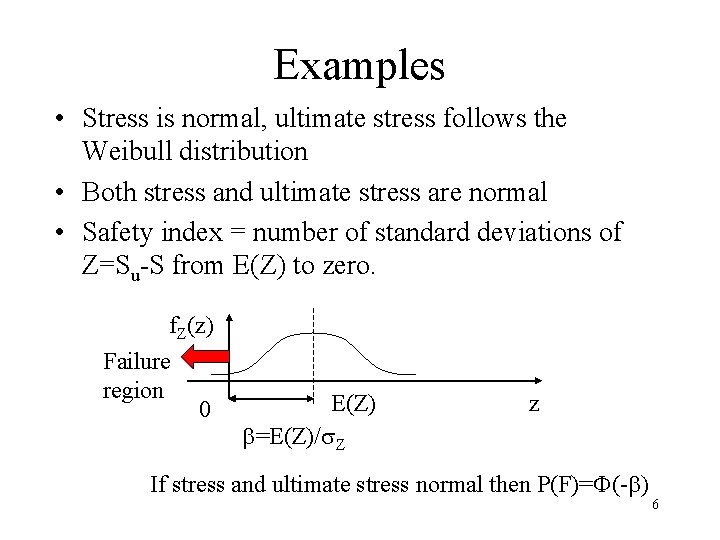
Examples • Stress is normal, ultimate stress follows the Weibull distribution • Both stress and ultimate stress are normal • Safety index = number of standard deviations of Z=Su-S from E(Z) to zero. f. Z(z) Failure region 0 E(Z) =E(Z)/ Z z If stress and ultimate stress normal then P(F)= (- ) 6

General method for calculation of failure probability Failure probability = integral of joint probability density function of random variables over failure region 7

Monte-Carlo simulation • Key idea: generate sample values of the uncertain variables on the computer, test if the system fails for each sample and approximate the probability of failure by the relative frequency of failure. 8

Standard Monte-Carlo simulation Define problem Estimate probability distribution of random variables Generate N sets of sample values of the random variables Calculate the performance function for each set P(F) = number of failures/N 9
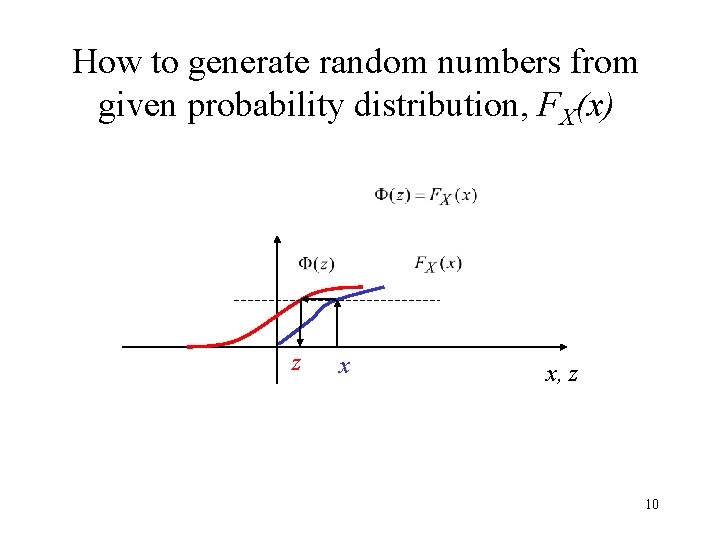
How to generate random numbers from given probability distribution, FX(x) z x x, z 10

Comments on standard Monte-Carlo simulation • Expensive, especially when failure probability is small (i. e. , 10 -6) • Often used to validate approximation of failure probability or to validate optimum design selected using approximate methods 11

Importance sampling • Reduces sample size required to estimate P(F) with given accuracy • Idea: generate random numbers from sampling density, f s, instead of true density, f • Sampling distribution is selected so as to generate many failures • Discount each failure according to ratio of true probability of occurrence to probability of occurrence based on sampling distribution 12

Importance sampling Define problem Estimate probability distribution of random variables, f Generate N sets of sample values random variables from sampling distribution f s Calculate the performance function for each set *Ii failure index function, 1 if failure occurs, 0 otherwise 13

Suggested reading • Ghiocel, D. , M. , “Stochastic Simulation Methods for Engineering Predictions, ” Engineering Design Reliability Handbook, CRC press, 2004, p. 20 -1. 14
- Slides: 14