6 QUANTUM MECHANICS AND ATOMIC STRUCTURE CHAPTER 6

6 QUANTUM MECHANICS AND ATOMIC STRUCTURE CHAPTER 6. 1 Quantum Picture of the Chemical Bond 6. 2 Exact Molecular Orbital for the Simplest Molecule: H 2+ 6. 3 Molecular Orbital Theory and the Linear Combination of Atomic Orbitals Approximation for H 2+ 6. 4 Homonuclear Diatomic Molecules: First-Period Atoms 6. 5 Homonuclear Diatomic Molecules: Second-Period Atoms 6. 6 Heteronuclear Diatomic Molecules 6. 7 Summary Comments for the LCAO Method and Diatomic Molecules General Chemistry I

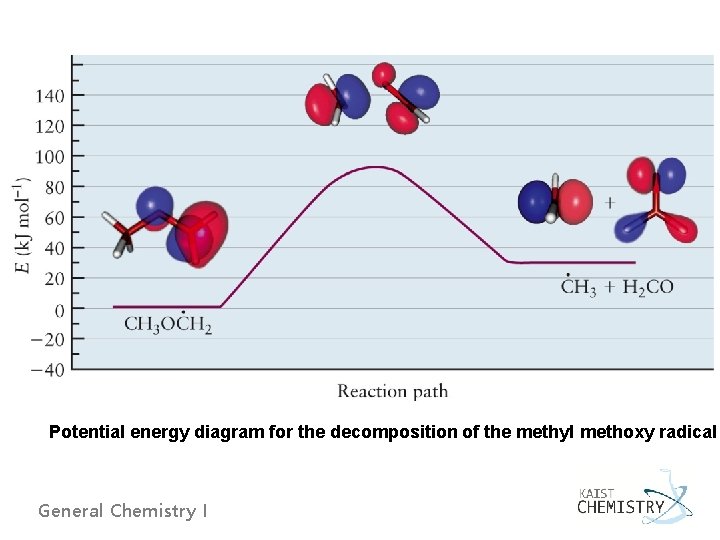
Potential energy diagram for the decomposition of the methyl methoxy radical General Chemistry I

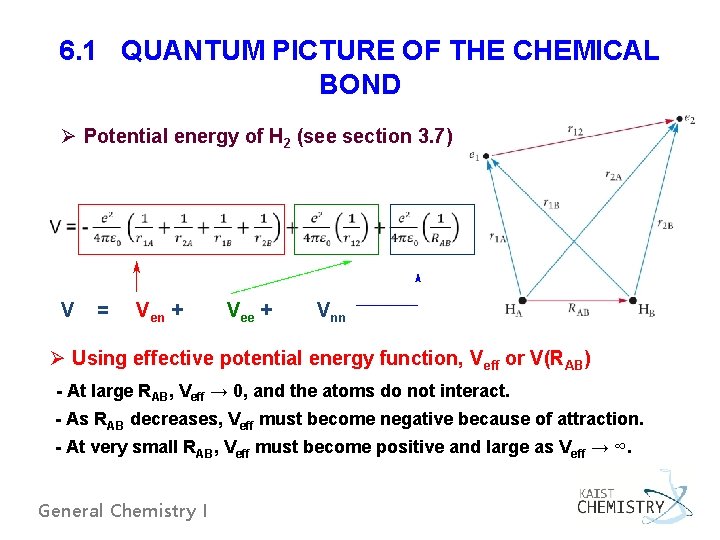
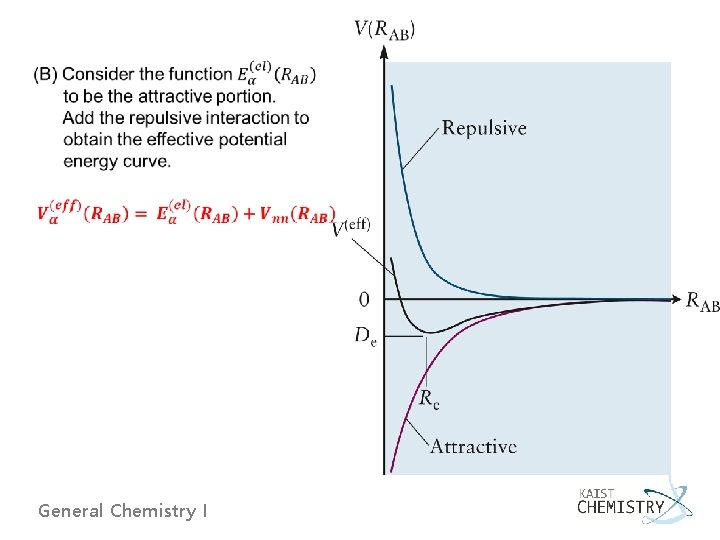
6. 1 QUANTUM PICTURE OF THE CHEMICAL BOND Ø Potential energy of H 2 (see section 3. 7) V = Ven + Vee + Vnn Ø Using effective potential energy function, Veff or V(RAB) - At large RAB, Veff → 0, and the atoms do not interact. - As RAB decreases, Veff must become negative because of attraction. - At very small RAB, Veff must become positive and large as Veff → ∞. General Chemistry I

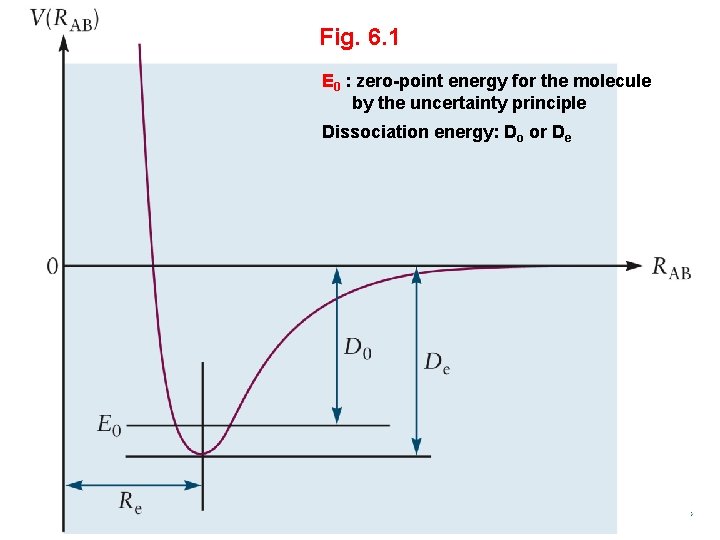
Fig. 6. 1 E 0 : zero-point energy for the molecule by the uncertainty principle Dissociation energy: Do or De General Chemistry I

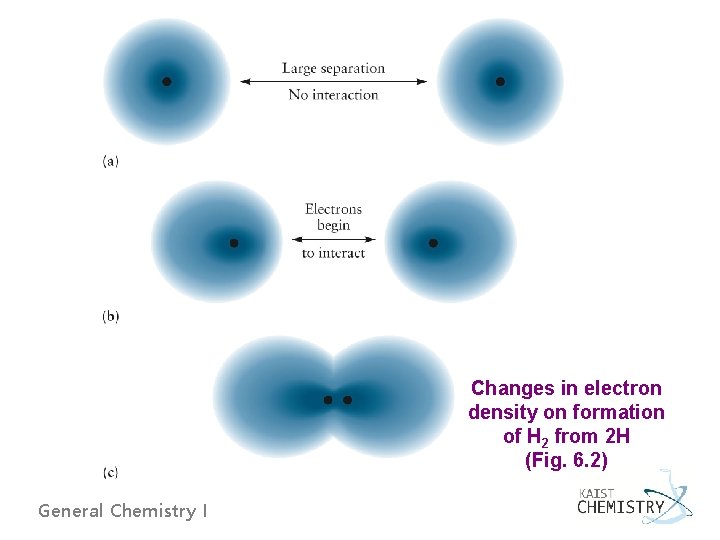
Changes in electron density on formation of H 2 from 2 H (Fig. 6. 2) General Chemistry I

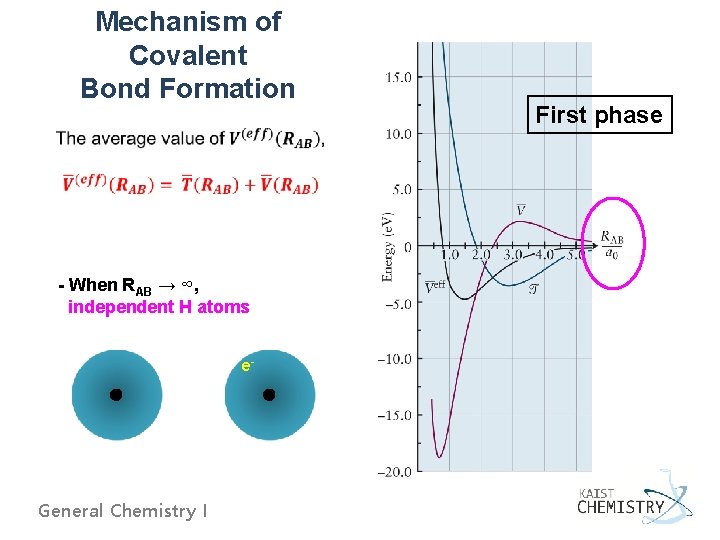
Born-Oppenheimer Approximation: Slow Nuclei, Fast Electrons - Nuclei are much more massive than the electrons, the nuclei in the molecules will move much more slowly than the electrons. → decoupling of the motions of the nuclei and the electrons (A) Consider the nuclei to be fixed at a specific set of positions. Then solve Schrödinger’s equation for the electrons moving around and obtain the energy levels and wave functions. Next, move the nuclei a bit, and repeat the calculation. Continue this procedure in steps. Each electronic energy level (E(el)a) is related to the nuclear coordinates, RAB. (a: the proper set of quantum numbers) General Chemistry I

General Chemistry I

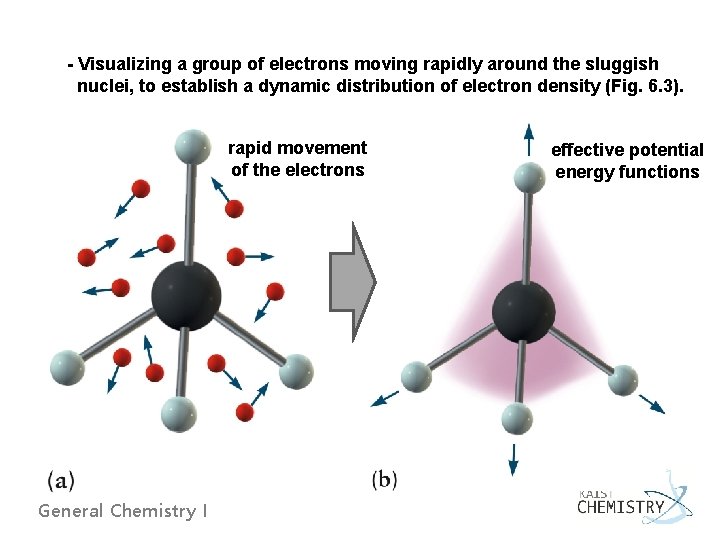
- Visualizing a group of electrons moving rapidly around the sluggish nuclei, to establish a dynamic distribution of electron density (Fig. 6. 3). rapid movement of the electrons General Chemistry I effective potential energy functions

Mechanism of Covalent Bond Formation - When RAB → ∞, independent H atoms e- General Chemistry I First phase

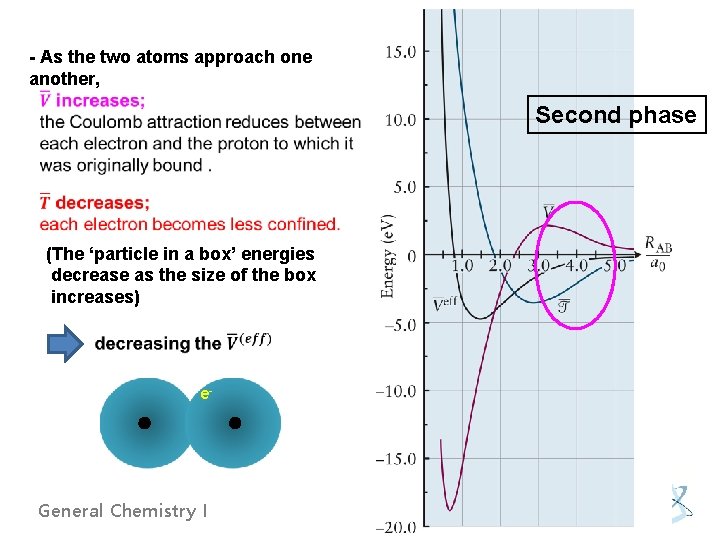
- As the two atoms approach one another, (The ‘particle in a box’ energies decrease as the size of the box increases) e- General Chemistry I Second phase

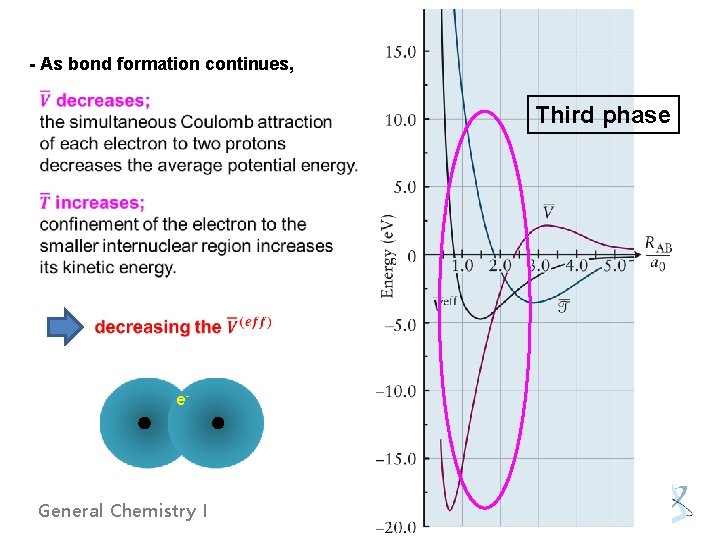
- As bond formation continues, Third phase e- General Chemistry I

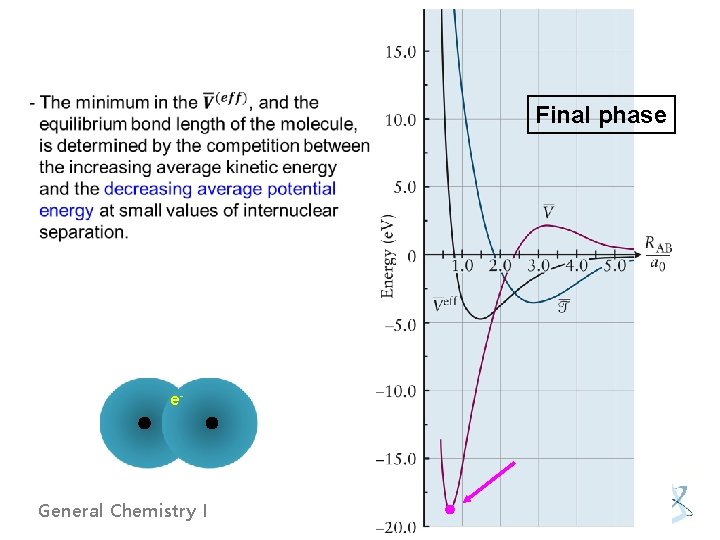
Final phase e- General Chemistry I

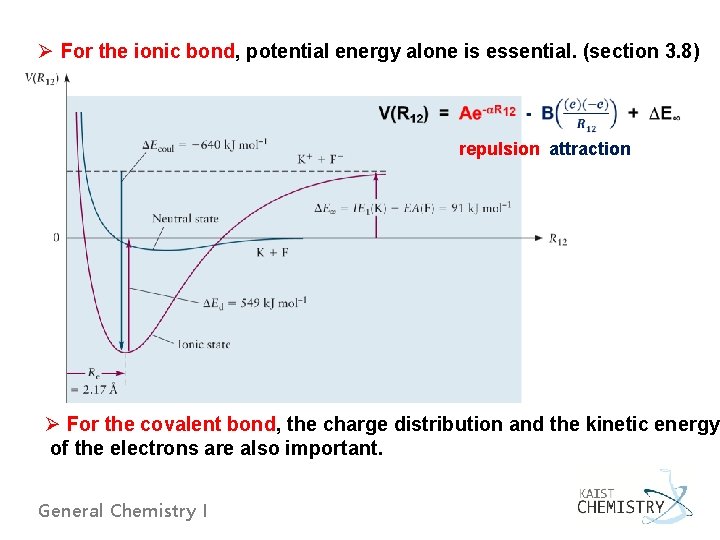
Ø For the ionic bond, potential energy alone is essential. (section 3. 8) repulsion attraction Ø For the covalent bond, the charge distribution and the kinetic energy of the electrons are also important. General Chemistry I

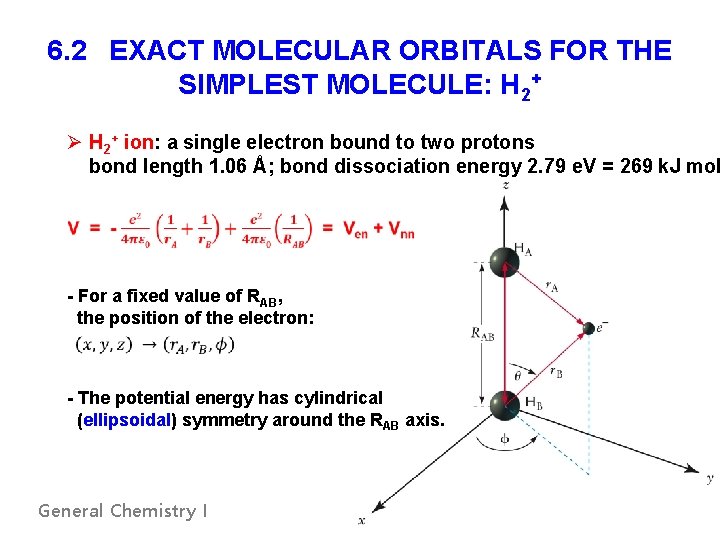
6. 2 EXACT MOLECULAR ORBITALS FOR THE SIMPLEST MOLECULE: H 2+ Ø H 2+ ion: a single electron bound to two protons bond length 1. 06 Å; bond dissociation energy 2. 79 e. V = 269 k. J mol - For a fixed value of RAB, the position of the electron: - The potential energy has cylindrical (ellipsoidal) symmetry around the RAB axis. General Chemistry I

Ø By the Born-Oppenheimer approximation, - RAB : holding at the equilibrium bond length of 1. 06 Å Omitting f due to the same potential energy for all values of f Ø The solution of the Schrödinger equation: - smooth, single-valued, and finite in all regions of space to define a probability density function of its square Solutions exists when the total energy and angular momentum are quantized. General Chemistry I

Electronic Wave Functions for H 2+ - isosurface comprising the wave function with 0. 1 of its maximum value. - red: + amplitude; blue: - amplitude - molecular orbital: each of exact one-electron wave functions General Chemistry I

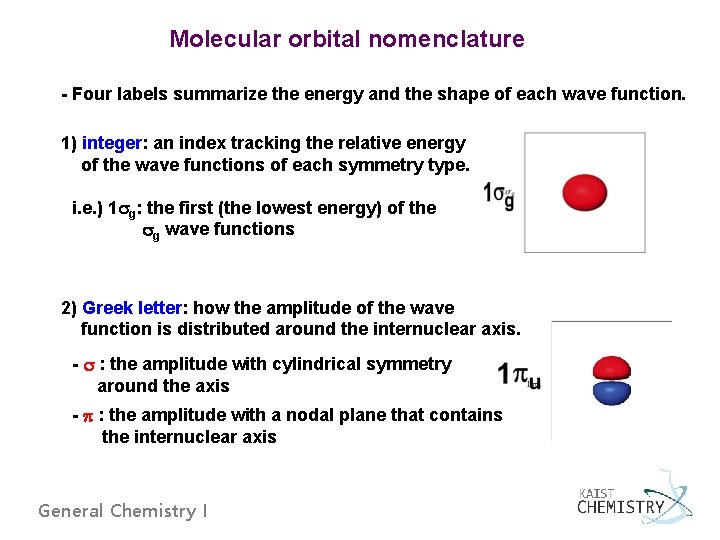
Molecular orbital nomenclature - Four labels summarize the energy and the shape of each wave function. 1) integer: an index tracking the relative energy of the wave functions of each symmetry type. i. e. ) 1 g: the first (the lowest energy) of the g wave functions 2) Greek letter: how the amplitude of the wave function is distributed around the internuclear axis. - : the amplitude with cylindrical symmetry around the axis - : the amplitude with a nodal plane that contains the internuclear axis General Chemistry I

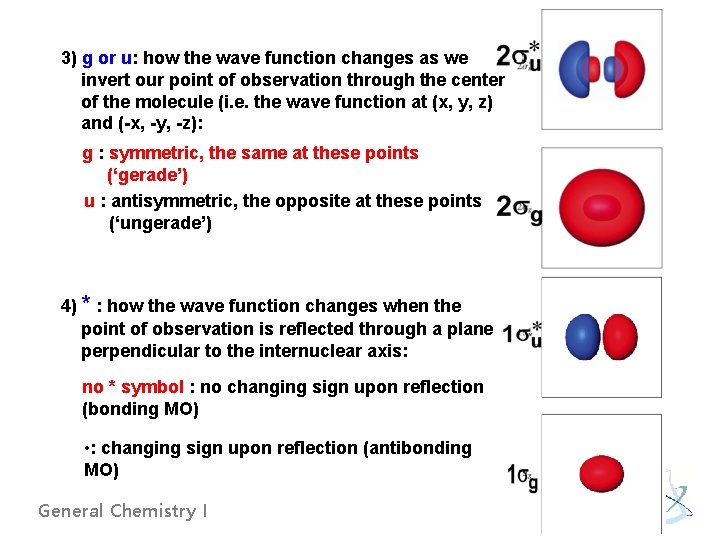
3) g or u: how the wave function changes as we invert our point of observation through the center of the molecule (i. e. the wave function at (x, y, z) and (-x, -y, -z): g : symmetric, the same at these points (‘gerade’) u : antisymmetric, the opposite at these points (‘ungerade’) 4) * : how the wave function changes when the point of observation is reflected through a plane perpendicular to the internuclear axis: no * symbol : no changing sign upon reflection (bonding MO) • : changing sign upon reflection (antibonding MO) General Chemistry I

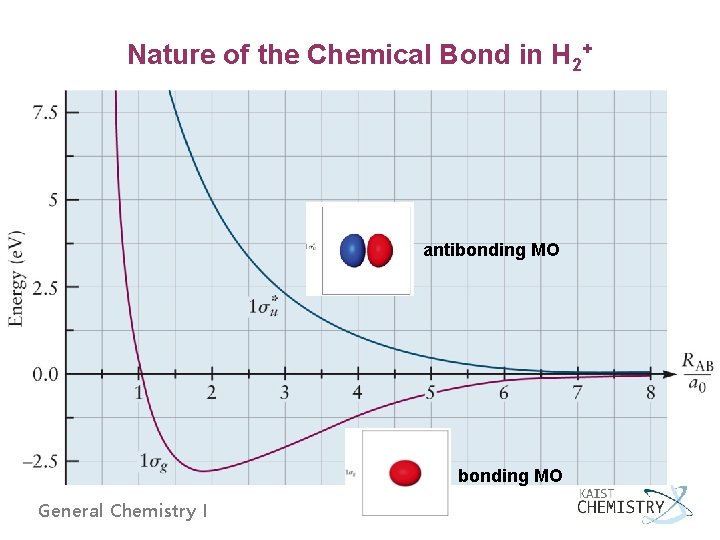
Nature of the Chemical Bond in H 2+ antibonding MO General Chemistry I

Summary of the Quantum Picture of Chemical Bonding for H 2+ 1. The Born-Oppenheimer approximation: fixing the nuclei positions 2. Molecular orbital: one-electron wave function, its square describes the distribution of electron density 3. Bonding MO: increased e density between the nuclei, decreased effective potential energy 4. Antibonding MO: a node on the internuclear axis, increased effective potential energy 5. orbital: cylindrical symmetry; cross-sections perpendicular to the internuclear axis are discs. 6. orbital: has a nodal plane containing the internuclear axis General Chemistry I

6. 3 MOLECULAR ORBITAL THEORY AND THE LINEAR COMBINATION OF ATOMIC ORBITALS APPROXIMATION FOR H 2+ Ø LCAO method: selecting sums and differences (linear combinations) of atomic orbital wave functions to generate the best approximation to each type of molecular orbital wave function - The general form for H 2+ General Chemistry I

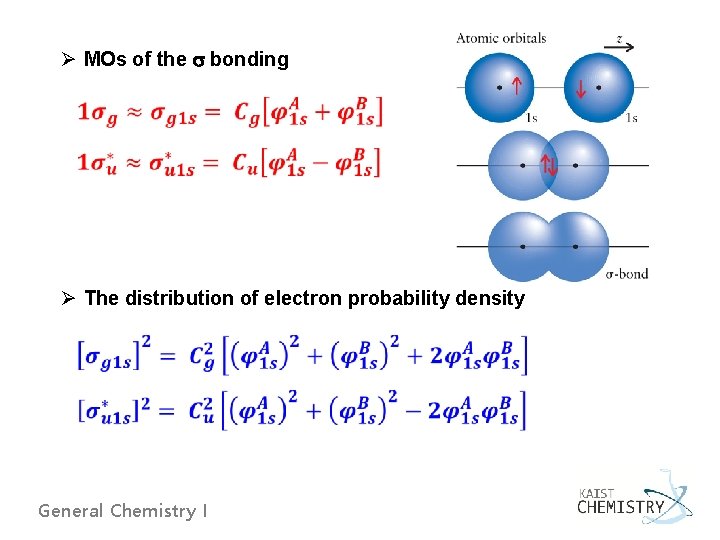
Ø MOs of the bonding Ø The distribution of electron probability density General Chemistry I

General Chemistry I

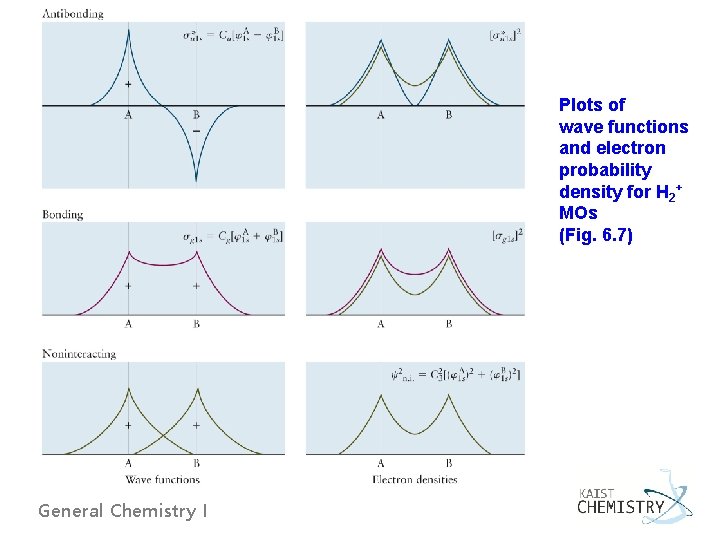
Plots of wave functions and electron probability density for H 2+ MOs (Fig. 6. 7) General Chemistry I

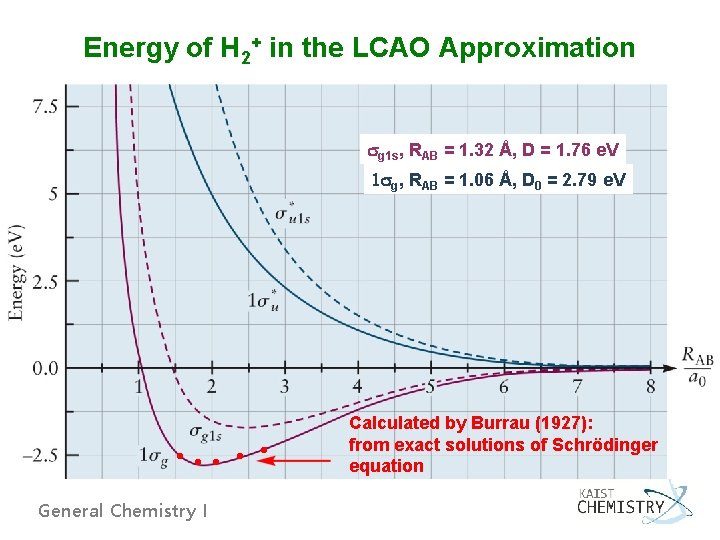
Energy of H 2+ in the LCAO Approximation g 1 s, RAB = 1. 32 Å, D = 1. 76 e. V 1 g, RAB = 1. 06 Å, D 0 = 2. 79 e. V Calculated by Burrau (1927): from exact solutions of Schrödinger equation General Chemistry I

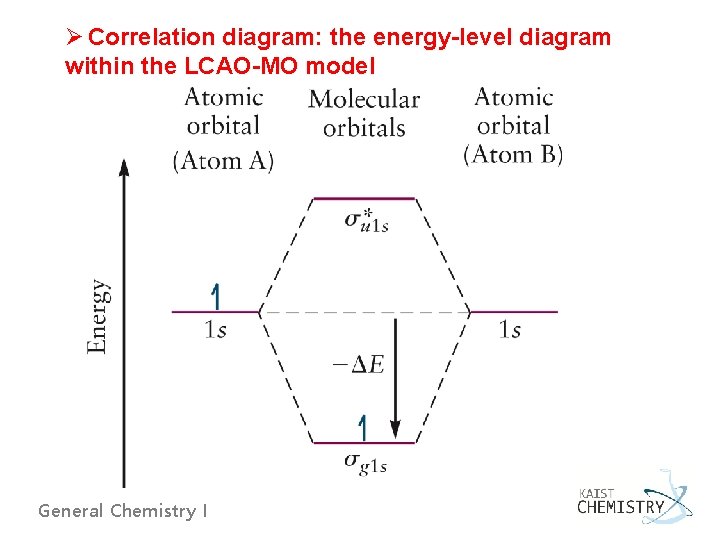
Ø Correlation diagram: the energy-level diagram within the LCAO-MO model General Chemistry I

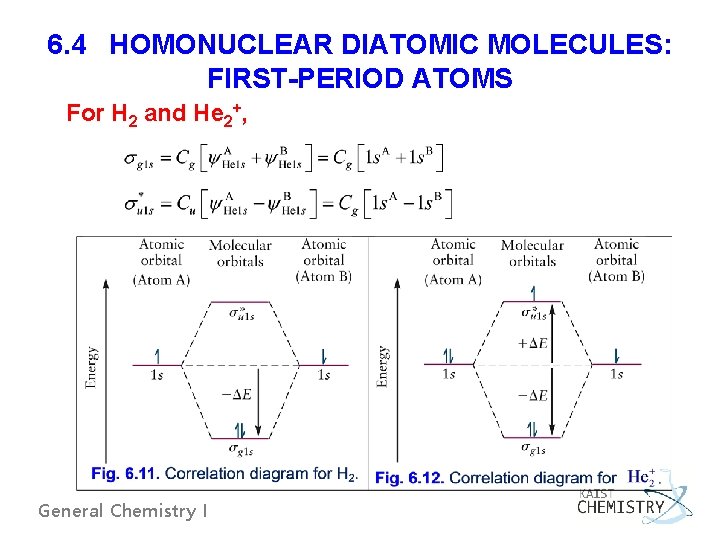
6. 4 HOMONUCLEAR DIATOMIC MOLECULES: FIRST-PERIOD ATOMS For H 2 and He 2+, General Chemistry I

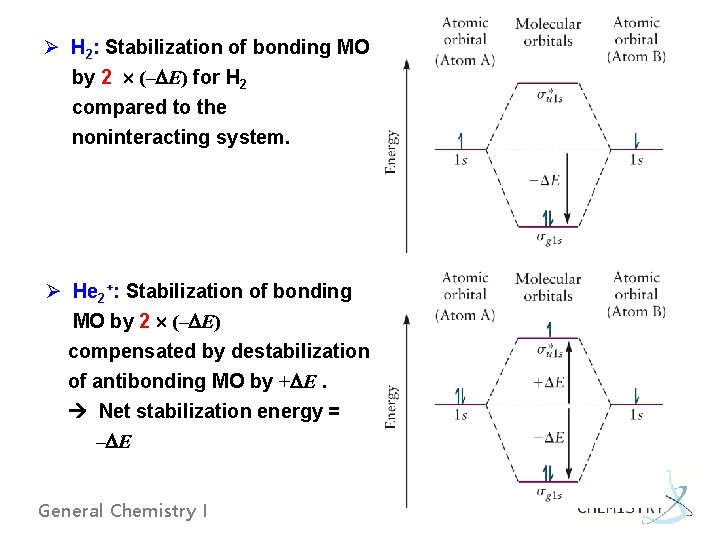
Ø H 2: Stabilization of bonding MO by 2 (– E) for H 2 compared to the noninteracting system. Ø He 2+: Stabilization of bonding MO by 2 (– E) compensated by destabilization of antibonding MO by + E. Net stabilization energy = – E General Chemistry I

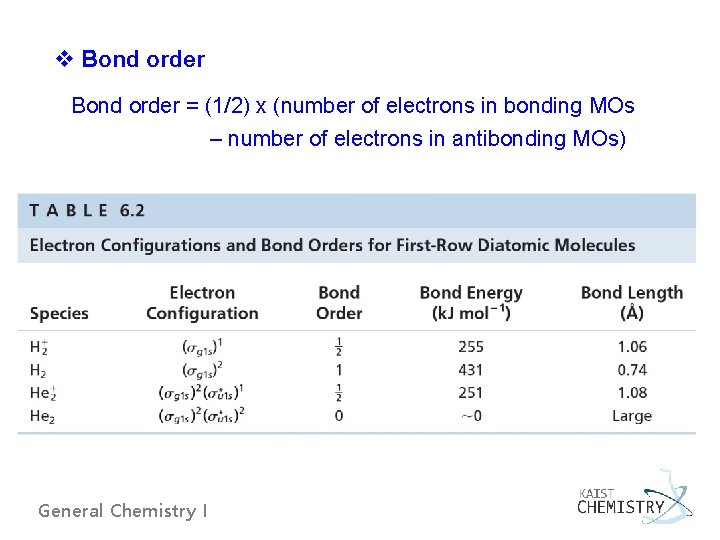
v Bond order = (1/2) x (number of electrons in bonding MOs – number of electrons in antibonding MOs) General Chemistry I

6. 5 HOMONUCLEAR DIATOMIC MOLECULES: SECOND-PERIOD ATOMS u LCAO-MO approximation Ø Combination of 2 s AOs to form g 2 s and u 2 s* MOs Ø Combination of 2 pz AOs to form and MOs The core 1 s 2 electrons are not included – they are too low in energy General Chemistry I

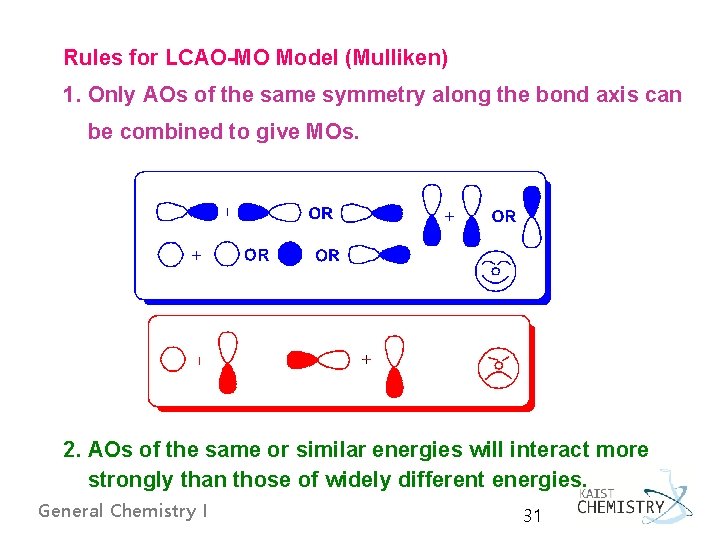
Rules for LCAO-MO Model (Mulliken) 1. Only AOs of the same symmetry along the bond axis can be combined to give MOs. 2. AOs of the same or similar energies will interact more strongly than those of widely different energies. General Chemistry I 31

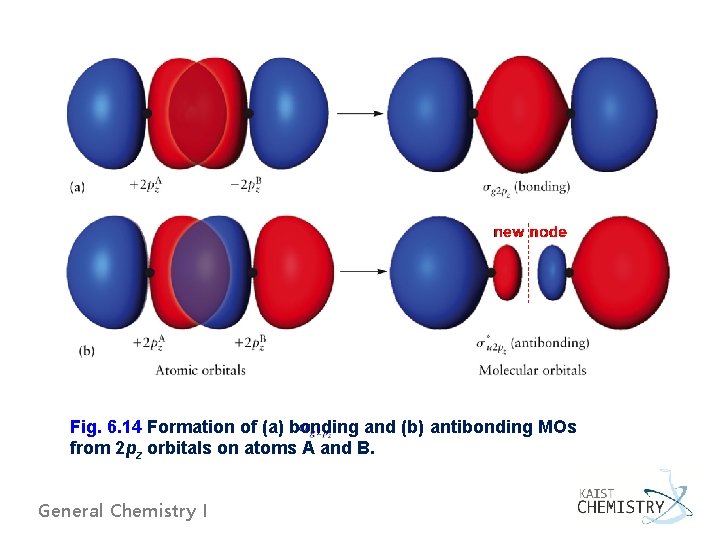
Fig. 6. 14 Formation of (a) bonding and (b) antibonding MOs from 2 pz orbitals on atoms A and B. General Chemistry I

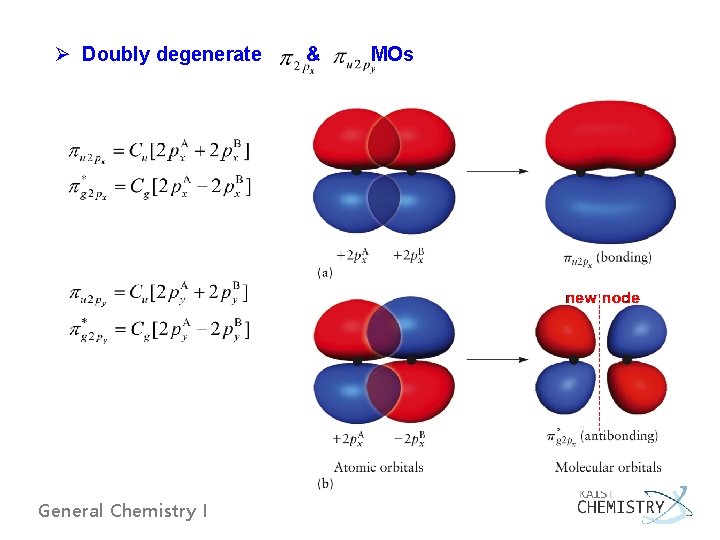
Ø Doubly degenerate General Chemistry I & MOs

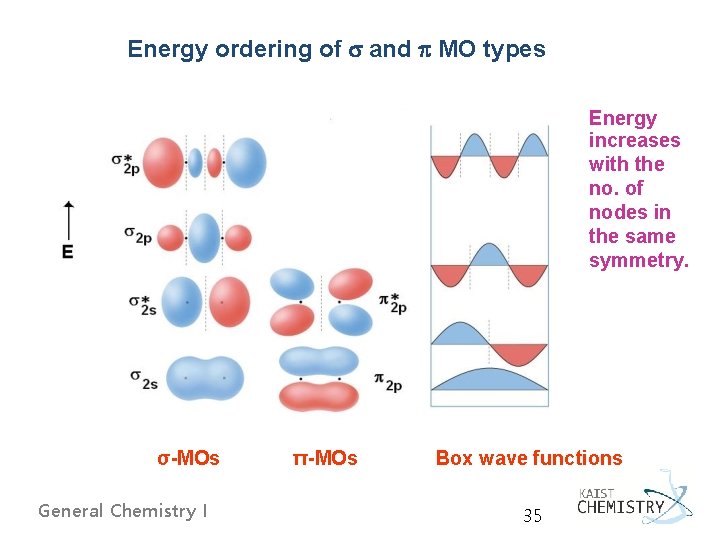
Ø Determination of energy ordering 1. Average energy of bonding-antibonding pair of MOs similar to that of original AO’s 2. Energy difference between a bonding-antibonding pair becomes large as the overlap of AO’s increases 3. Rule of thumb 1: bonding MOs < antibonding MOs 4. Rule of thumb 2: energy increases with number of nodes 5. Ordering for -group: 2 s < 2 s* < 2 p* (see slide 35) 6. Ordering for -group: 2 p < 2 p* (see slide 35) 7. For ordering and , experimental results must be invoked: 2 p < 2 p, 2 p* < 2 p* for all the 2 nd-row molecules (except O 2 and F 2) 2 p < 2 p, 2 p* < 2 p* for O 2 and F 2 (see slide 36, etc) General Chemistry I

Energy ordering of and MO types Energy increases with the no. of nodes in the same symmetry. σ-MOs General Chemistry I π-MOs Box wave functions 35

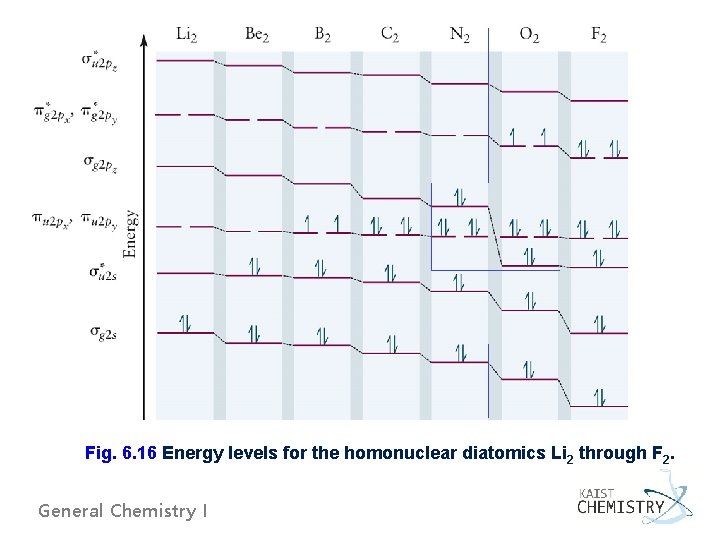
Fig. 6. 16 Energy levels for the homonuclear diatomics Li 2 through F 2. General Chemistry I

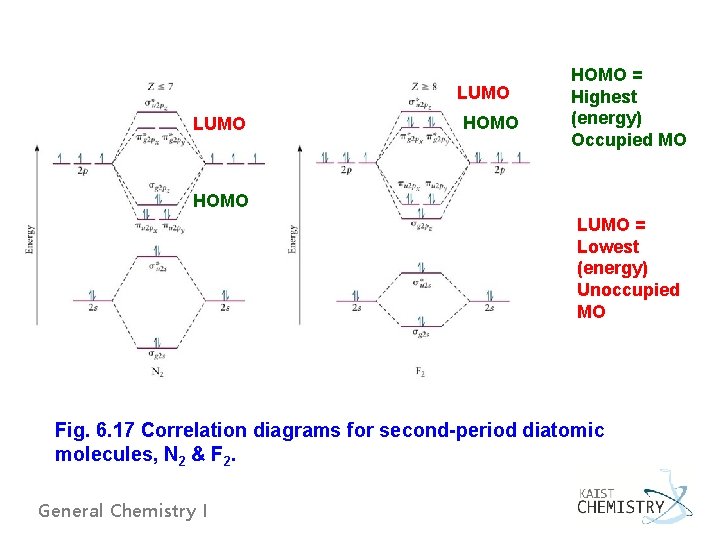
LUMO HOMO = Highest (energy) Occupied MO HOMO LUMO = Lowest (energy) Unoccupied MO Fig. 6. 17 Correlation diagrams for second-period diatomic molecules, N 2 & F 2. General Chemistry I

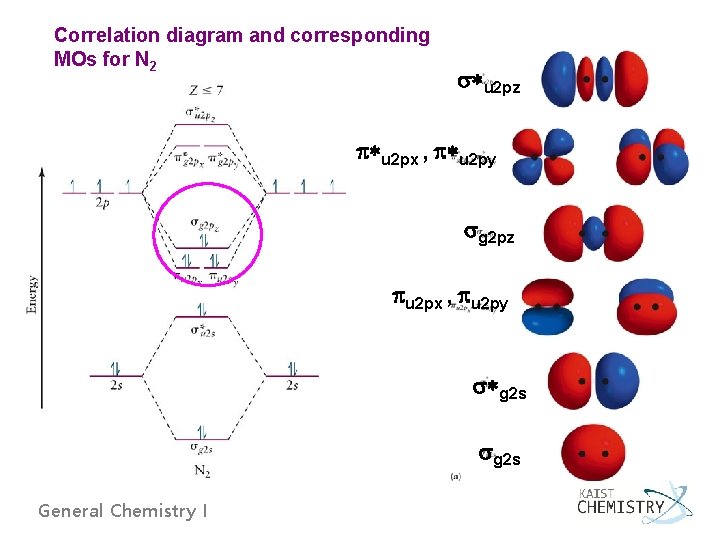
Correlation diagram and corresponding MOs for N 2 *u 2 pz *u 2 px , *u 2 py g 2 pz u 2 px , u 2 py *g 2 s General Chemistry I

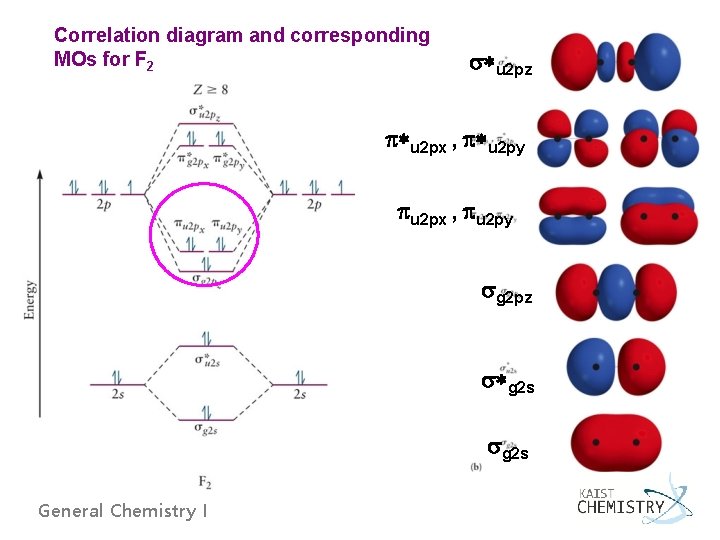
Correlation diagram and corresponding MOs for F 2 *u 2 pz *u 2 px , *u 2 py u 2 px , u 2 py g 2 pz *g 2 s General Chemistry I

u Cross-over in the correlation diagrams of Li 2~N 2 and O 2~Ne 2 Ø Reversed ordering of energy for Li 2 ~ N 2 ~ Due to large electron-electron spatial repulsions between electrons in and MO’s. Ø Normal ordering of energy for O 2, F 2, Ne 2 ~ As Z increases, the repulsion decreases since electrons in MO’s are drawn more strongly toward the nucleus. General Chemistry I 40

Fig. 6. 18 (a) Paramagnetic liquid oxygen, O 2, and (b) diamagnetic liquid nitrogen, N 2, pours straight between the poles of a magnet. General Chemistry I

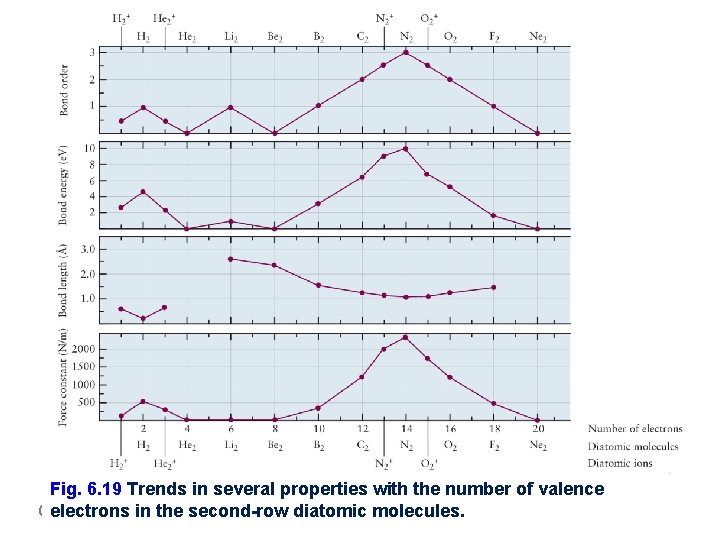
Fig. 6. 19 Trends in several properties with the number of valence electrons in the second-row diatomic molecules. General Chemistry I

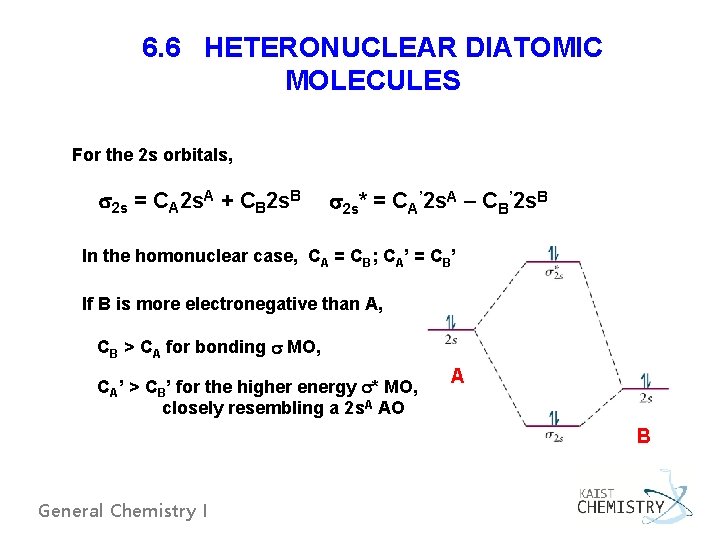
6. 6 HETERONUCLEAR DIATOMIC MOLECULES For the 2 s orbitals, 2 s = CA 2 s. A + CB 2 s. B 2 s* = CA’ 2 s. A – CB’ 2 s. B In the homonuclear case, CA = CB; CA’ = CB’ If B is more electronegative than A, CB > CA for bonding MO, CA’ > CB’ for the higher energy * MO, closely resembling a 2 s. A AO A B General Chemistry I

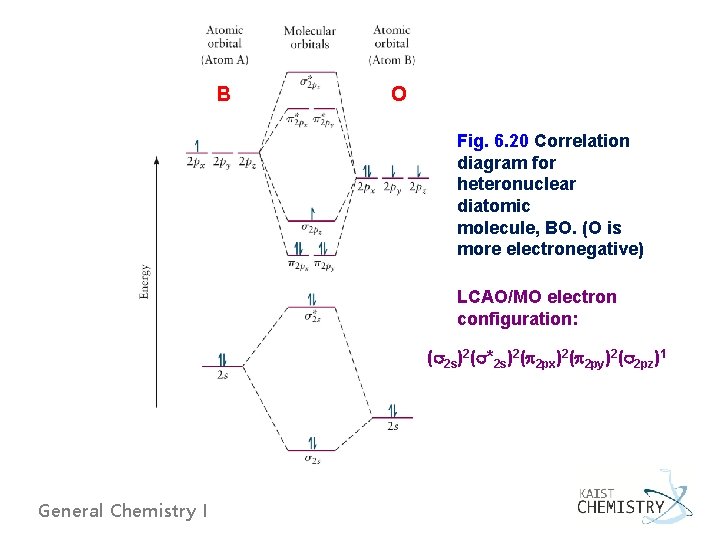
B O Fig. 6. 20 Correlation diagram for heteronuclear diatomic molecule, BO. (O is more electronegative) LCAO/MO electron configuration: ( 2 s)2( *2 s)2( 2 px)2( 2 py)2( 2 pz)1 General Chemistry I

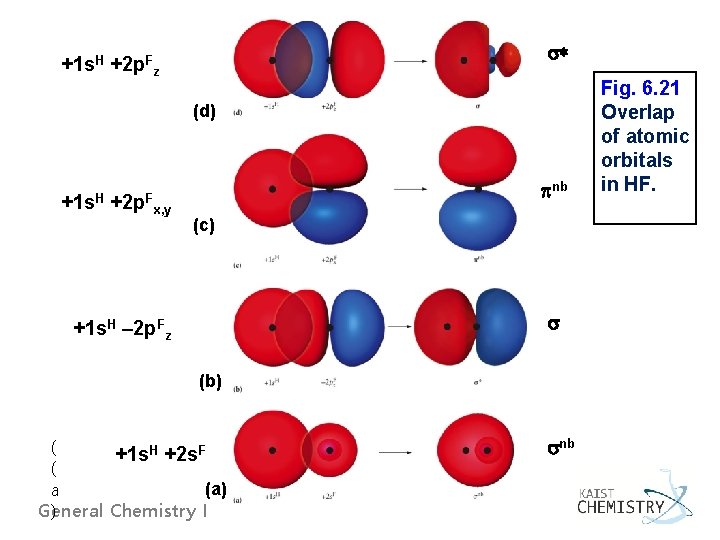
* +1 s. H +2 p. Fz (d) +1 s. H +2 p. F nb x, y (c) +1 s. H – 2 p. Fz (b) ( +1 s. H +2 s. F ( (a) a General Chemistry I ) nb Fig. 6. 21 Overlap of atomic orbitals in HF.

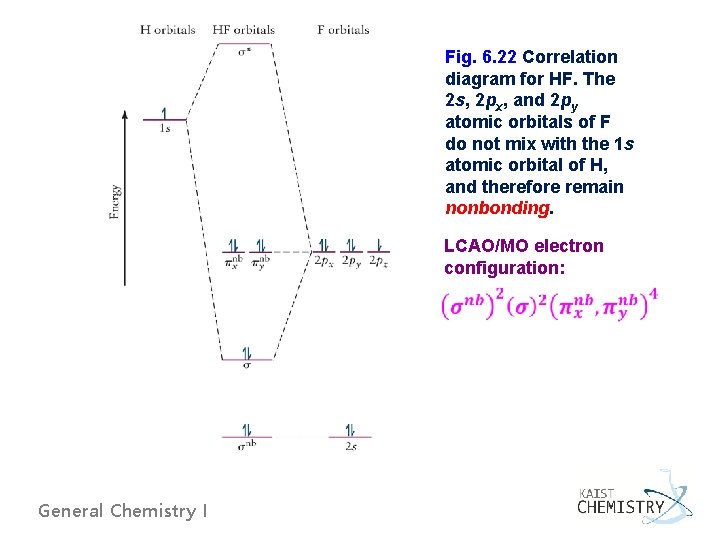
Fig. 6. 22 Correlation diagram for HF. The 2 s, 2 px, and 2 py atomic orbitals of F do not mix with the 1 s atomic orbital of H, and therefore remain nonbonding. LCAO/MO electron configuration: General Chemistry I

6. 7 SUMMARY COMMENTS FOR THE LCAOMO METHOD AND DIATOMIC MOLECULES The qualitative LCAO-MO method easily identifies the sequence of energy levels for a molecule, such as trends in bond length and bond energy, but does not give their specific values. The qualitative energy level diagram is very useful for interpreting experiments that involve adsorption and emission of energy such as spectroscopy, ionization by electron removal, and electron attachment. General Chemistry I

6 QUANTUM MECHANICS AND ATOMIC STRUCTURE CHAPTER 6. 8 Valence Bond Theory and the Electron Pair Bond 6. 9 Orbital Hybridization for Polyatomic Molecules 6. 10 Predicting Molecular Structures and Shapes 6. 11 Using the LCAO and Valence Bond Methods Together 6. 12 Summary and Comparison of the LCAO and Valence Bond Methods 6. 13 A Deeper Look (Properties of Exact Molecular Orbitals for H 2+) General Chemistry I

6. 8 VALENCE BOND THEORY AND THE ELECTRON PAIR BOND Ø Explains the Lewis electron pair model Ø VB wave function for the bond is a product of two one-electron AO wave functions Ø Easily describes structure and geometry of bonds in polyatomic molecules General Chemistry I

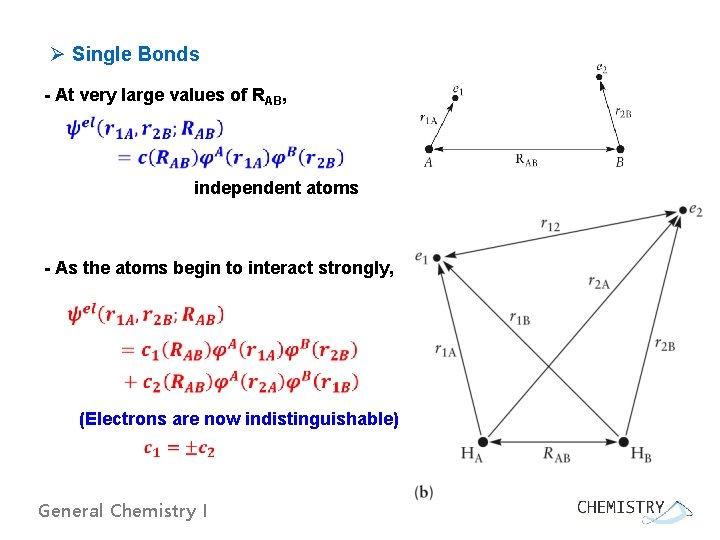
Ø Single Bonds - At very large values of RAB, independent atoms - As the atoms begin to interact strongly, (Electrons are now indistinguishable) General Chemistry I

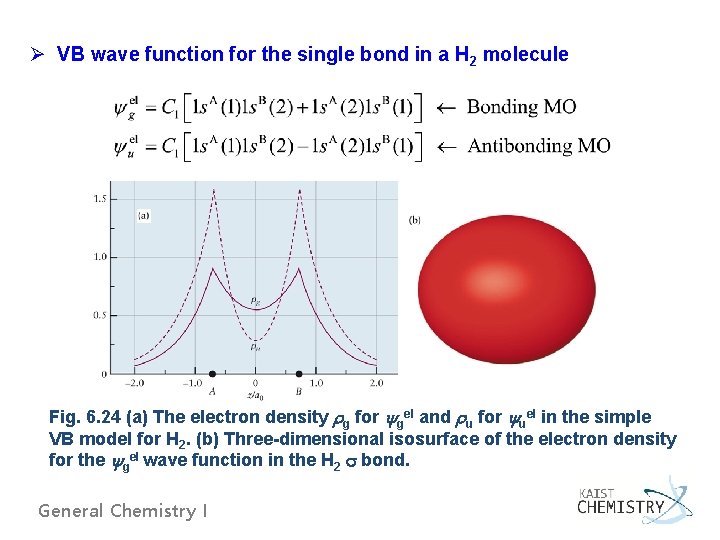
Ø VB wave function for the single bond in a H 2 molecule Fig. 6. 24 (a) The electron density g for gel and u for uel in the simple VB model for H 2. (b) Three-dimensional isosurface of the electron density for the gel wave function in the H 2 bond. General Chemistry I

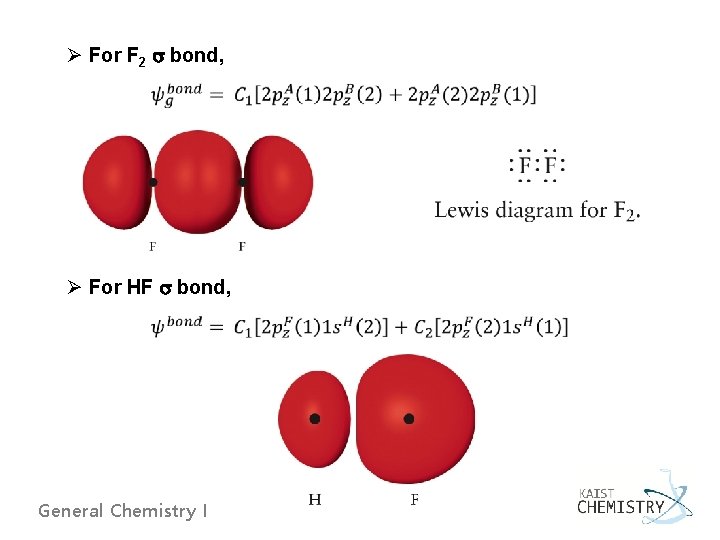
Ø For F 2 bond, Ø For HF bond, General Chemistry I

Ø Multiple Bonds N: (1 s)2(2 px)1(2 py)1(2 pz)1 General Chemistry I

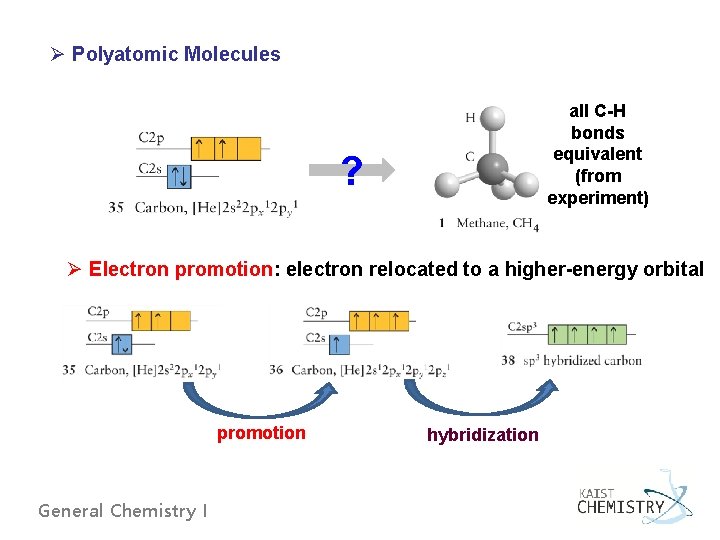
Ø Polyatomic Molecules all C-H bonds equivalent (from experiment) ? Ø Electron promotion: electron relocated to a higher-energy orbital promotion General Chemistry I hybridization

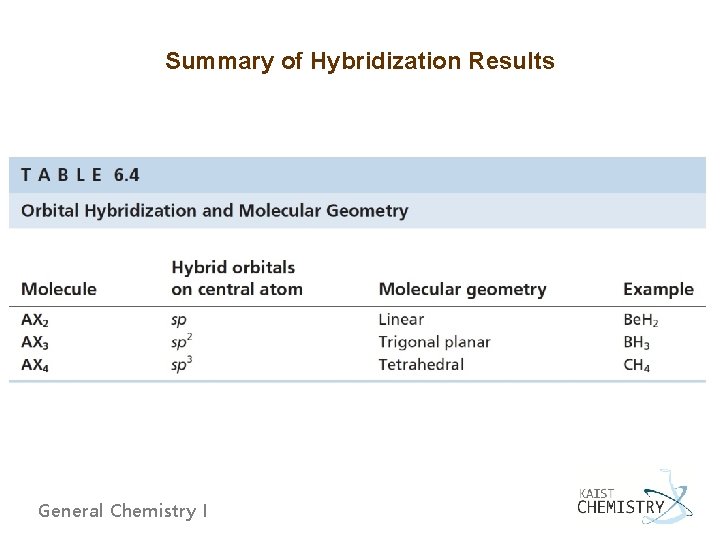
6. 9 ORBITAL HYBRIDIZATION FOR POLYATOMIC MOLECULES Ø sp-Hybridization Be. H 2 Promotion: Be: (1 s)2(2 s)2 Be: (1 s)2(2 s)1(2 pz)1 Two equivalent sp hybrid orbitals: and New electronic configuration, Be: (1 s)2( 1)1( 2)1 Wave functions for the two bonding pairs of electrons: A pair of bonds at an angle 180 o apart linear molecule General Chemistry I

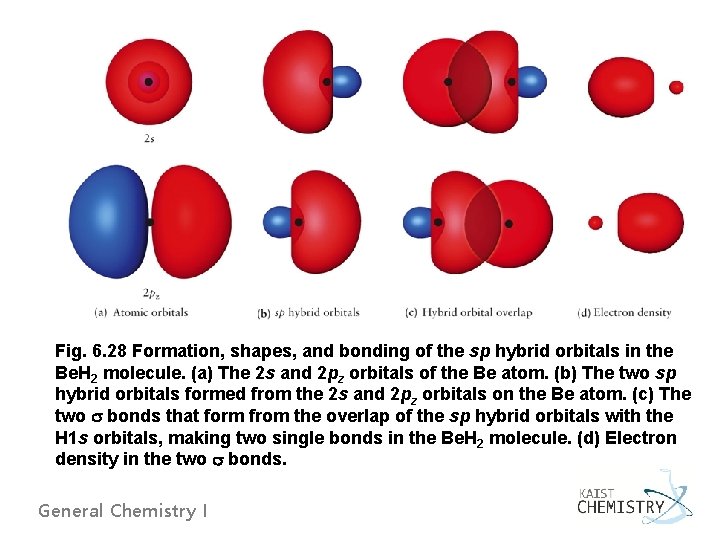
Fig. 6. 28 Formation, shapes, and bonding of the sp hybrid orbitals in the Be. H 2 molecule. (a) The 2 s and 2 pz orbitals of the Be atom. (b) The two sp hybrid orbitals formed from the 2 s and 2 pz orbitals on the Be atom. (c) The two bonds that form from the overlap of the sp hybrid orbitals with the H 1 s orbitals, making two single bonds in the Be. H 2 molecule. (d) Electron density in the two bonds. General Chemistry I

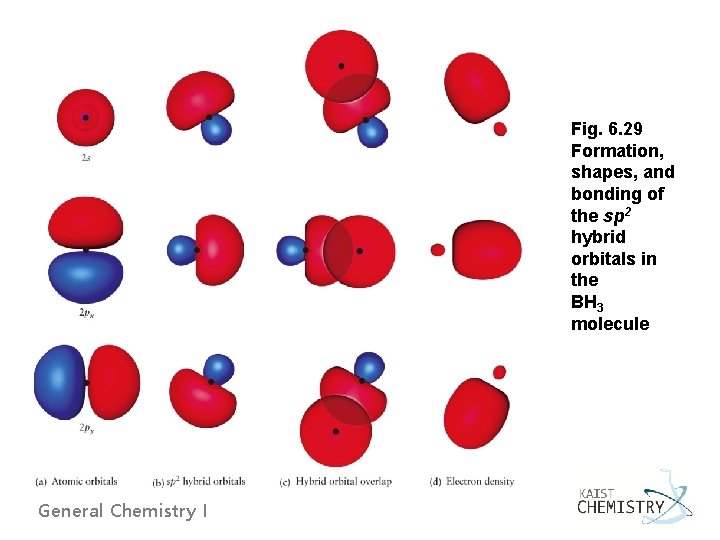
Ø sp 2 -Hybridization BH 3 Promotion: B: (1 s)2(2 px)1 B: (1 s)2(2 s)1(2 px)1(2 py)1 Three equivalent sp 2 hybrid orbitals: New electronic configuration, B: (1 s)2( 1)1( 2)1( 3)1 Three bonds at an angle 120 o in a plane trigonal planar General Chemistry I

Fig. 6. 29 Formation, shapes, and bonding of the sp 2 hybrid orbitals in the BH 3 molecule General Chemistry I

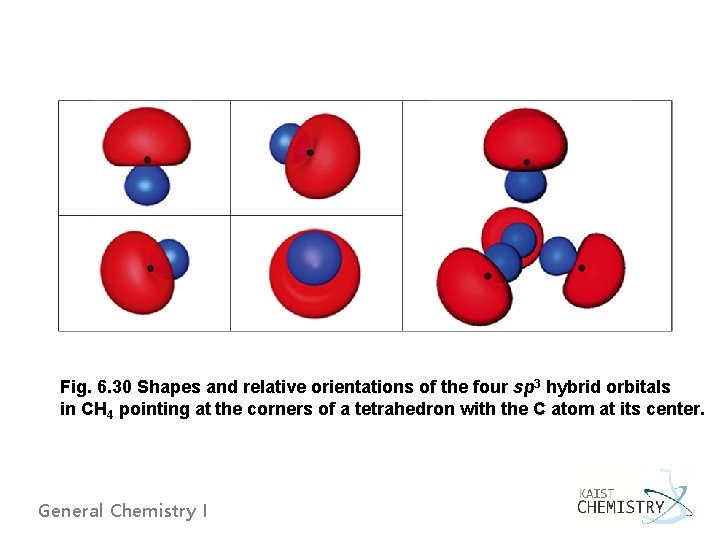
Ø sp 3 -Hybridization CH 4 Promotion: C: (1 s)2(2 px)1(2 py)1 C: (1 s)2(2 s)1(2 px)1(2 py)1(2 pz)1 Four equivalent sp 3 hybrid orbitals: New electronic configuration, C: (1 s)2( 1)1( 2)1( 3)1 ( 4)1 Four bonds at an angle 109. 5 o generating tetrahedral geometry General Chemistry I

Fig. 6. 30 Shapes and relative orientations of the four sp 3 hybrid orbitals in CH 4 pointing at the corners of a tetrahedron with the C atom at its center. General Chemistry I

Summary of Hybridization Results General Chemistry I

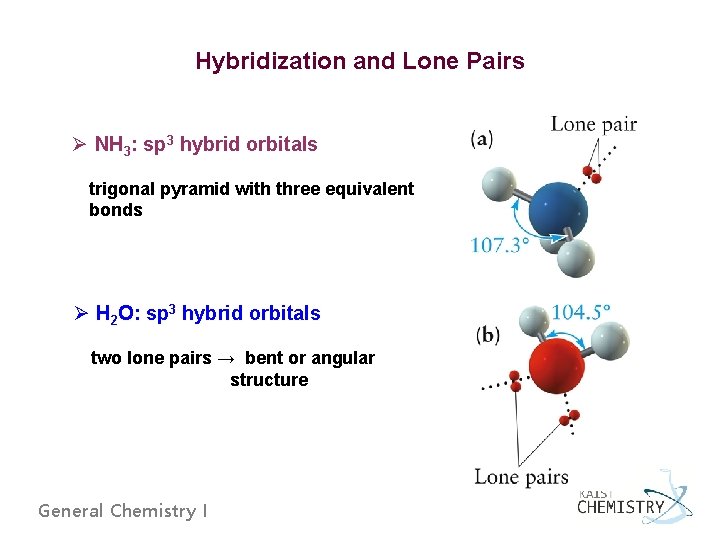
Hybridization and Lone Pairs Ø NH 3: sp 3 hybrid orbitals trigonal pyramid with three equivalent bonds Ø H 2 O: sp 3 hybrid orbitals two lone pairs → bent or angular structure General Chemistry I

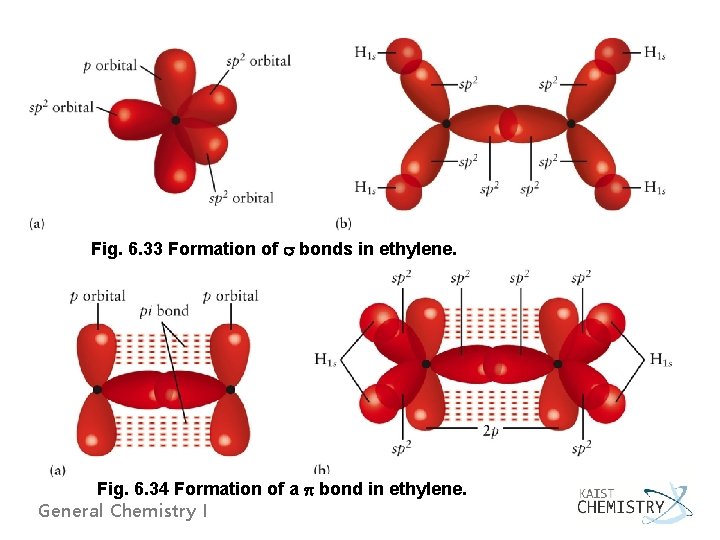
Ø Multiple Bonds in Organic Compounds v Ethylene, C 2 H 4 Promotion, C: (1 s)2(2 px)1(2 py)1 C: (1 s)2(2 s)1(2 px)1(2 py)1(2 pz)1 Formation of three sp 2 hybrid orbitals from the 2 s and two 2 p orbitals New electronic configuration, C: (1 s)2( 1)1( 2)1( 3)1(2 pz)1 Five bonds: C 1 1 -H 1 s, C 1 2 -H 1 s, C 2 1 -H 1 s, C 1 3 - C 2 3 One bond: C 12 pz-C 22 pz One double bond (C=C): (C 1 3 - C 2 3) + (C 12 pz-C 22 pz) Note: = sp 2 General Chemistry I

Fig. 6. 33 Formation of bonds in ethylene. Fig. 6. 34 Formation of a bond in ethylene. General Chemistry I

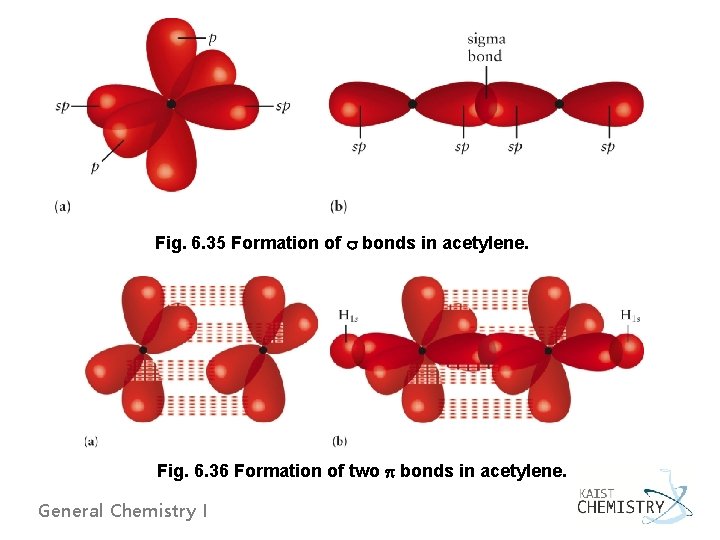
v Acetylene, C 2 H 2 Linear, triple bond, H-C-C bond angles of 180 o Promotion, C: (1 s)2(2 px)1(2 py)1 C: (1 s)2(2 s)1(2 pz)1(2 px)1(2 py)1 Formation of two sp hybrid orbitals from the 2 s and the 2 pz orbitals New electronic configuration, C: (1 s)2( 1)1( 2)1(2 px)1(2 py)1 Three bonds: C 1 1 -H 1 s, C 2 1 -H 1 s, C 1 2 - C 2 2 Two bonds: C 12 px-C 22 px, C 12 py-C 22 py One triple bond : (C 1 2 - C 2 2) + (C 12 px-C 22 px, C 12 py-C 22 py) Note: = sp General Chemistry I

Fig. 6. 35 Formation of bonds in acetylene. Fig. 6. 36 Formation of two bonds in acetylene. General Chemistry I

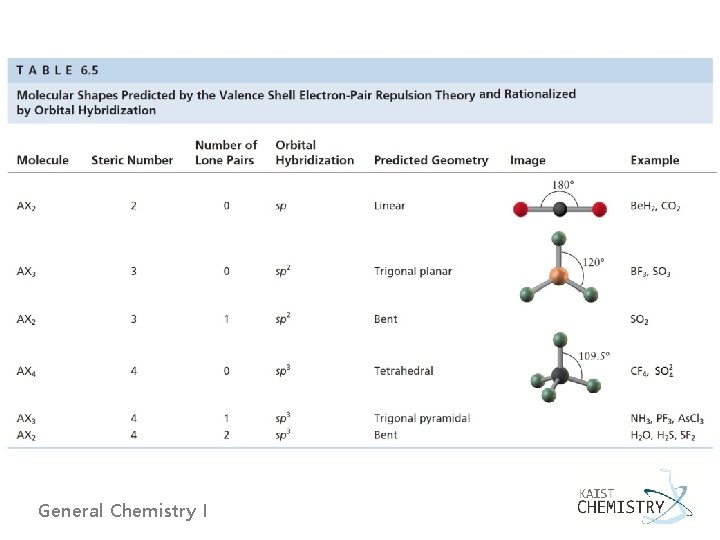
6. 10 PREDICTING MOLECULAR STRUCTURES AND SHAPE Ø Description of the structure and shape of a molecule (1) Determine the empirical formula. (2) Determine the molecular formula. (3) Determine the structural formula from a Lewis diagram. (4) Determine the molecular shape from experiments. (5) Identify the hybridization scheme that best explains the shape predicted by VSEPR. General Chemistry I

EXAMPLE 6. 4 Hydrazine: Elemental analysis shows its mass per cent composition to be 87. 419% nitrogen and 12. 581% hydrogen. The density of hydrazine at 1 atm And 25 o. C is 1. 31 g. L-1. Determine the molecular formula for hydrazine. Predict the structure of hydrazine. What is the hybridization of the N atoms? (1) Elemental analysis: N(87. 419%), H (12. 581%) (2) Empirical formula: NH 2 (Molar mass)emp (3) Molar mass calculated from the ideal gas law (with known ) (4) Molar mass / (Molar mass)emp = 2, Molecular formula: N 2 H 4 (5) Lewis diagram, steric number (4) sp 3 hybrid orbitals General Chemistry I

General Chemistry I

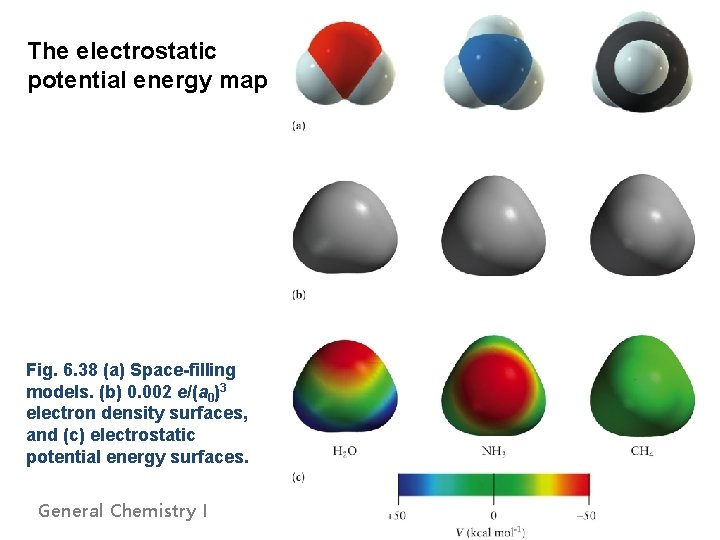
The electrostatic potential energy map Fig. 6. 38 (a) Space-filling models. (b) 0. 002 e/(a 0)3 electron density surfaces, and (c) electrostatic potential energy surfaces. General Chemistry I

6. 11 USING THE LCAO AND VALENCE BOND METHODS TOGETHER u Linear Triatomic Molecules (CO 2, N 2 O, NO 2+) Ø Central atom sp hybridization from s and pz orbitals Two sp orbitals form bonds with outer atoms Remaining px and py orbitals form bonds Ø bonds pz orbital (outer atom) with sp hybrid (central atom) Ø bonds linear combinations of the px (or py) orbitals give bonding, antibonding, and nonbonding General Chemistry I

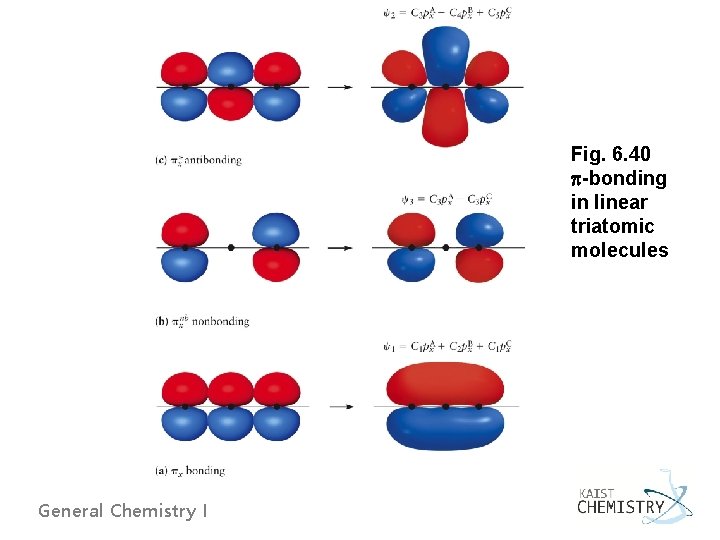
Fig. 6. 40 -bonding in linear triatomic molecules General Chemistry I

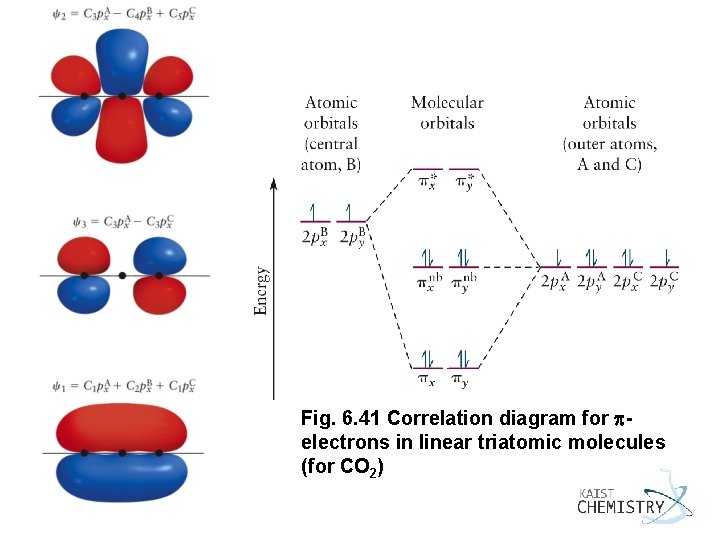
Fig. 6. 41 Correlation diagram for electrons in linear triatomic molecules (for CO 2) General Chemistry I

u Nonlinear Triatomic Molecules (NO 2, O 3, NF 2, NO 2 -) Ø Central atom sp 2 hybridization from s, px, and py orbitals One of sp 2 orbitals holds a lone pair Two of sp 2 orbitals form bonds with outer atoms Remaining pz orbital forms bond Ø Outer atom p orbital pointing toward the central atom forms a bond pz orbital forms a bond with pz orbitals of other atoms Remaining p orbital and s orbital nonbonding General Chemistry I

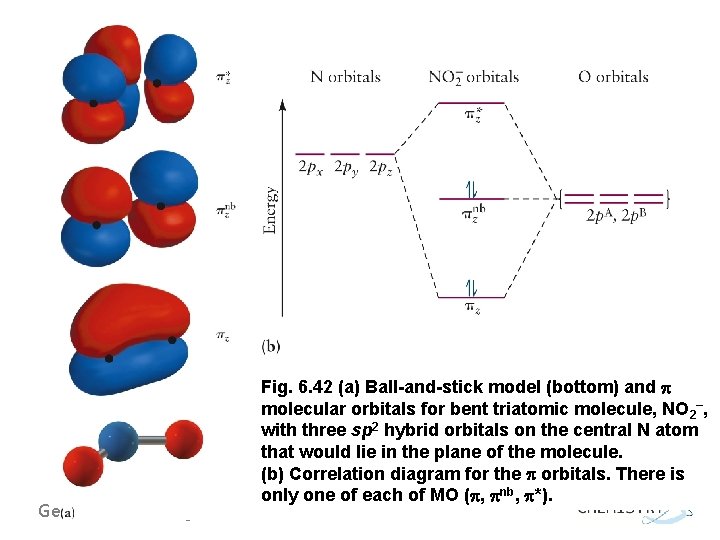
General Chemistry I Fig. 6. 42 (a) Ball-and-stick model (bottom) and molecular orbitals for bent triatomic molecule, NO 2–, with three sp 2 hybrid orbitals on the central N atom that would lie in the plane of the molecule. (b) Correlation diagram for the orbitals. There is only one of each of MO ( , nb, *).

6. 12 SUMMARY AND COMPARISON OF THE LCAO AND VALENCE BOND METHODS Ø LCAO method for H 2 forming a bond: Ø Molecular electronic wave function in the LCAO approximation: General Chemistry I

Ø Molecular electronic wave function in the VB model: Ø Comparison of MO and VB theories: purely covalent structure H–H v Improved VB wavefunction: General Chemistry I mixture of ionic states, HA-HB+ and HA+HBThis is over-emphasized in original LCAO-MO method and is absent in original VB model

General Chemistry I

10 Problem Sets For Chapter 6, 2, 18, 28, 48, 52, 58, 62, 64, 66, 72 General Chemistry I