6 Quadratic Equations l Equations involving three terms








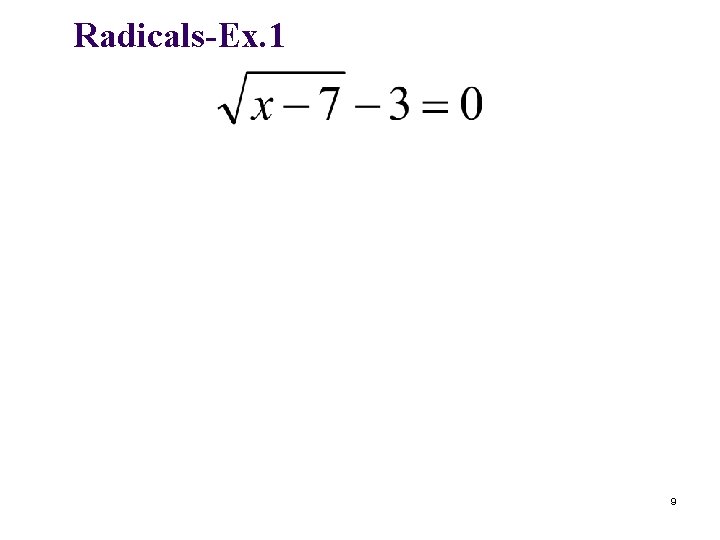





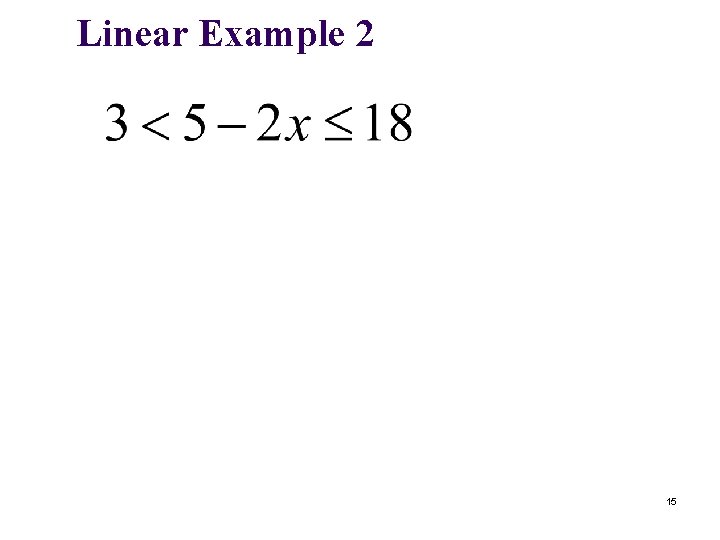



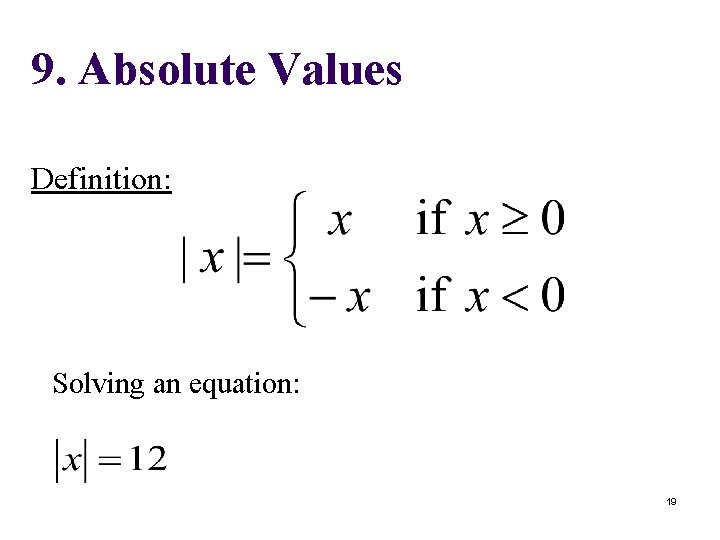
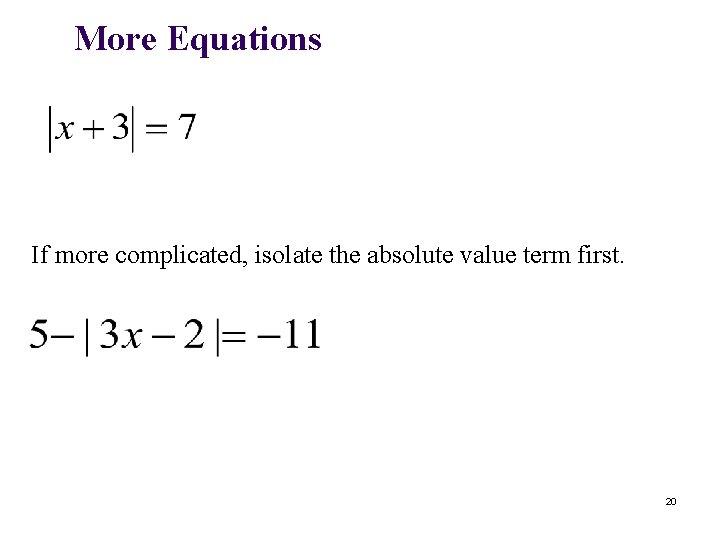
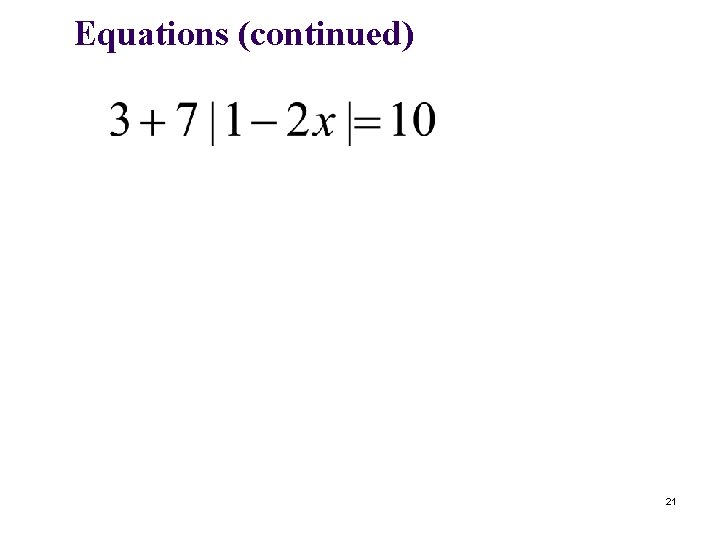

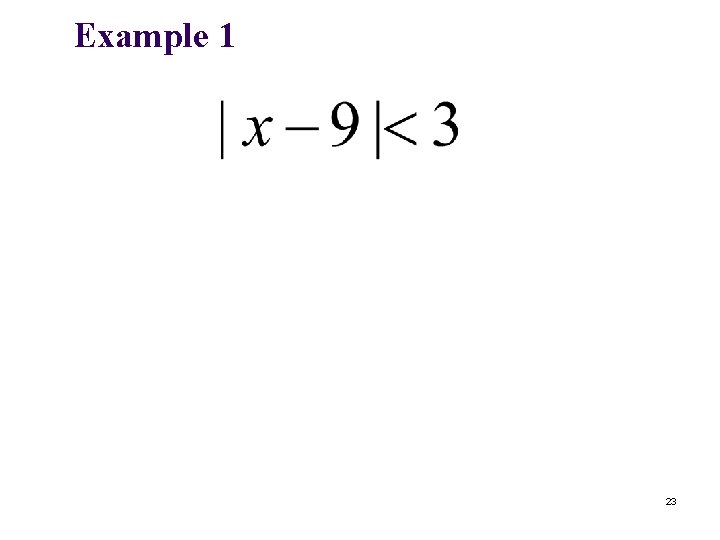

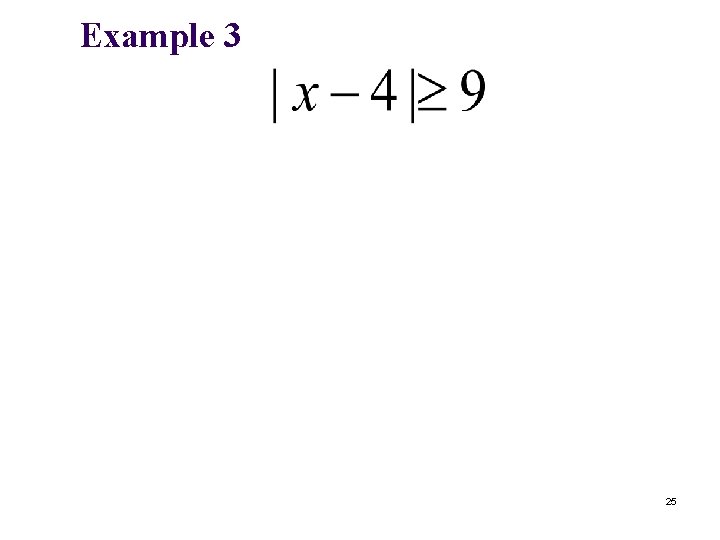
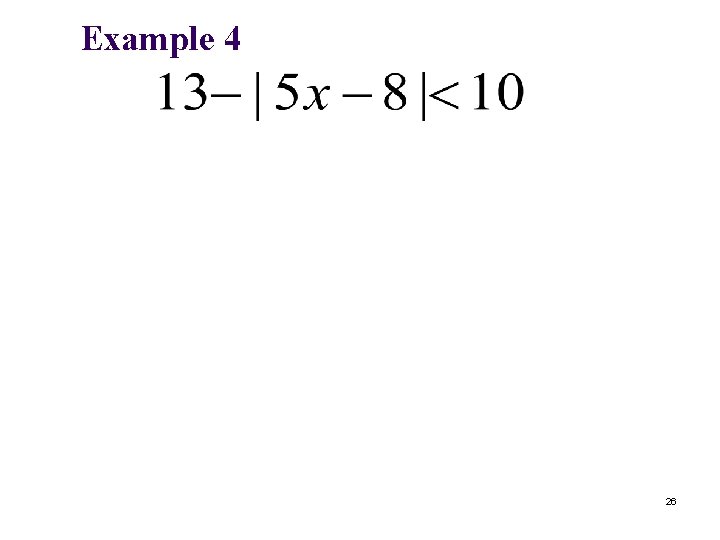
- Slides: 26

6. Quadratic Equations l Equations involving three terms constant, linear, and square l Take square root, factor or use quadratic formula l 1

Factoring Since AB = 0 implies either A=0 or B = 0, then rewrite the quadratic equation as a product of linear factors. 2

Factoring 3

Quadratic Formula If factoring not nice, remember quadratic formula: For given quadratic equation, find solutions for x with: x= 4

Examples: 5

Application A rectangular garden is 8 feet longer than it is wide. If its area is 240 square feet, then what are its dimensions? Quantities looking for: 6

7. Other Types of Equations Polynomials-Ex. 1 7

Polynomials-Ex. 2 8
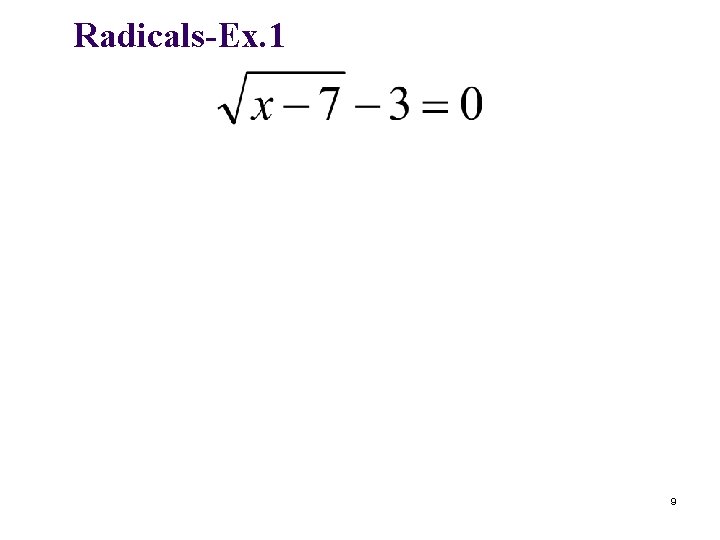
Radicals-Ex. 1 9

Radicals-Ex. 2 10

Quadratic Type – Ex. 1 Find all real solutions: Quadratic Type: a(something)2 + b(something) + constant = 0 11

Quadratic Type – Ex. 2 Find all real solutions: Quadratic Type: a(something)2 + b(something) + constant = 0 12

8. Inequalities Basic Rules: Adding, subtracting, multiplying by a positive constant does not change direction. 13

Linear Example 1 14
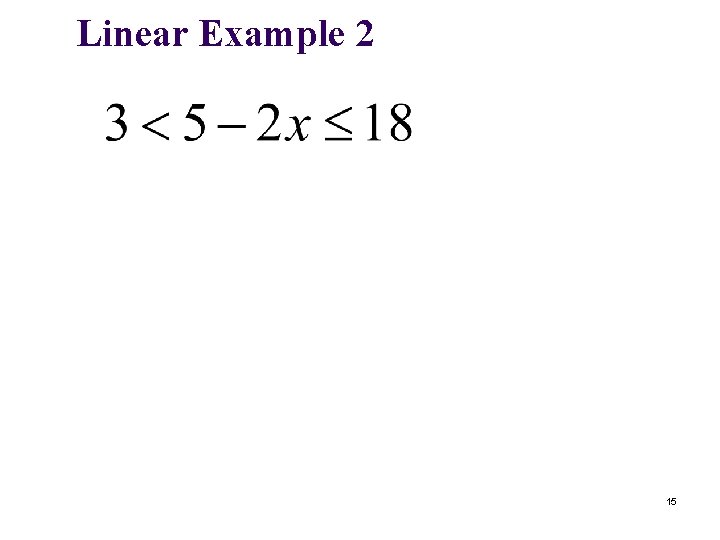
Linear Example 2 15

Nonlinear Example 1 Cut number line up according to linear factors. What makes each factor equal zero? What is the product at those values? Pick one value in each piece of the number line. What is the product at each of those values? Which pieces satisfy the inequality? 16

Nonlinear Example 2 Cut number line up according to each linear factor. What makes each factor equal zero? What is the quotient at those values? Pick one value in each piece of the number line. What is the quotient at each of those values? Which pieces satisfy the inequality? 17

Application A telephone company offers two calling plans. Plan A: $25 per month and $0. 05 per minute Plan B: $7 per month and $0. 11 per minute For how many minutes would plan B be cheaper? 18
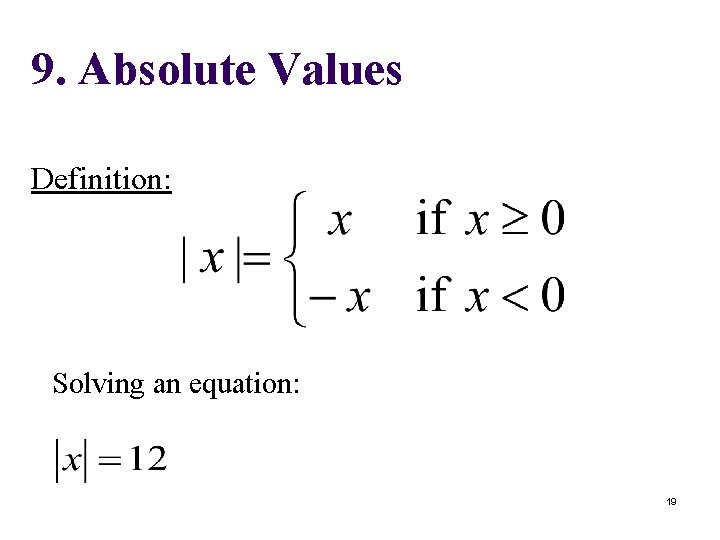
9. Absolute Values Definition: Solving an equation: 19
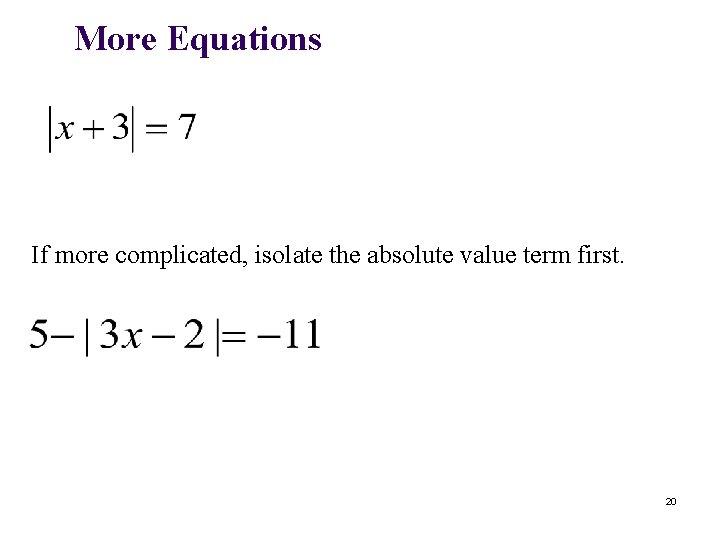
More Equations If more complicated, isolate the absolute value term first. 20
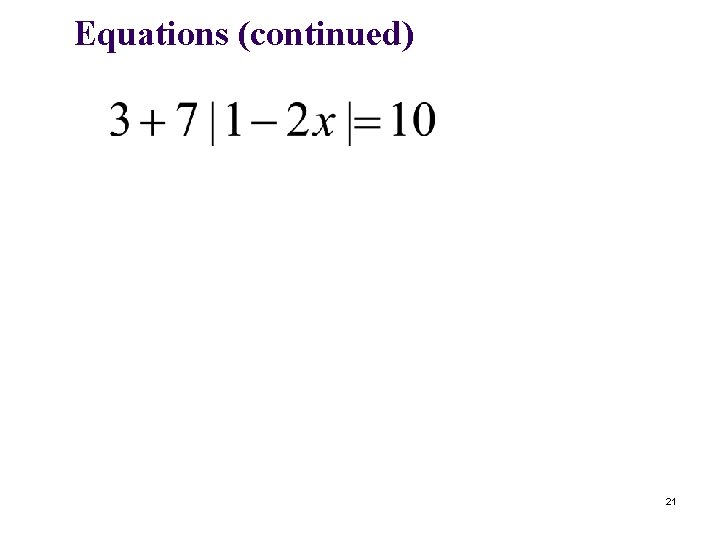
Equations (continued) 21

Possible Inequalities • | x | < c means -c < x < c • | x | c means -c x c • | x | > c means x > c or x < -c • | x | c means x c or x -c 22
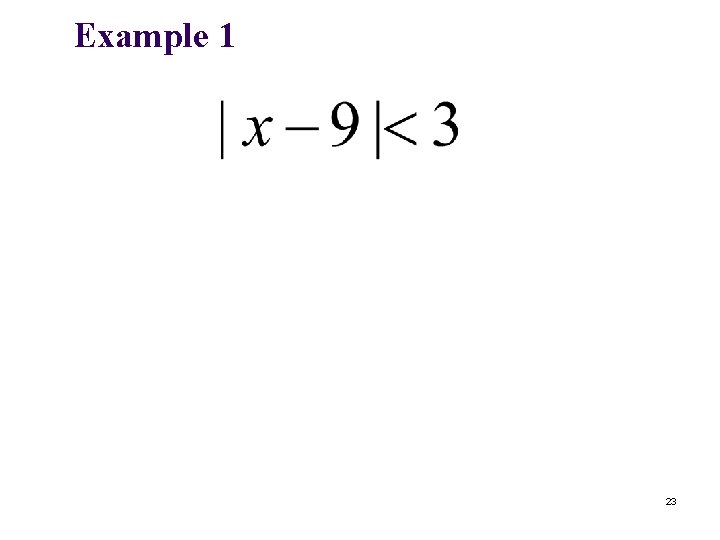
Example 1 23

Example 2 24
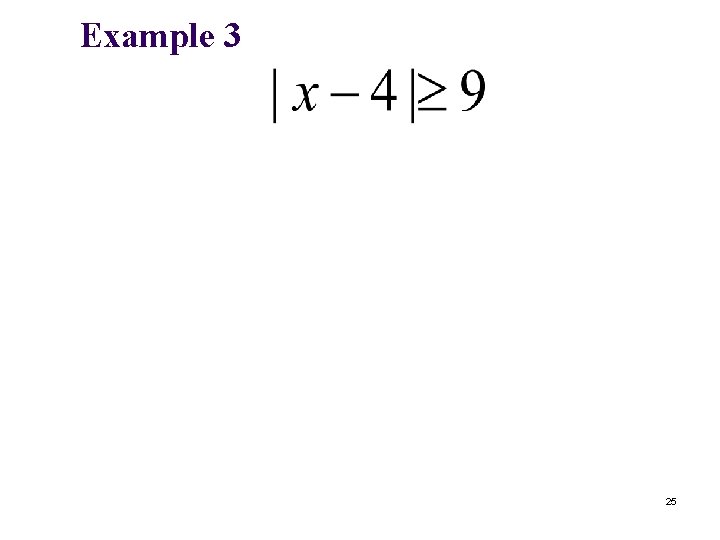
Example 3 25
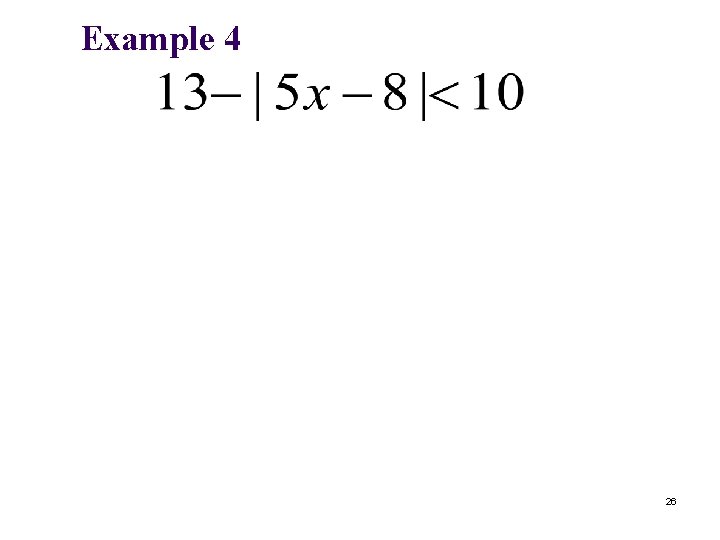
Example 4 26