6 minutes WarmUp For each parabola find an

6 minutes Warm-Up For each parabola, find an equation for the axis of symmetry and the coordinates of the vertex. State whether the parabola opens up or down, and whether the y -coordinate of the vertex is the minimum or maximum value of the function. 1) 2)

9. 2 Parabolas Objectives: • Write and graph the standard equation of a parabola given sufficient information • Given an equation of a parabola, graph it and label the vertex, focus, and directrix

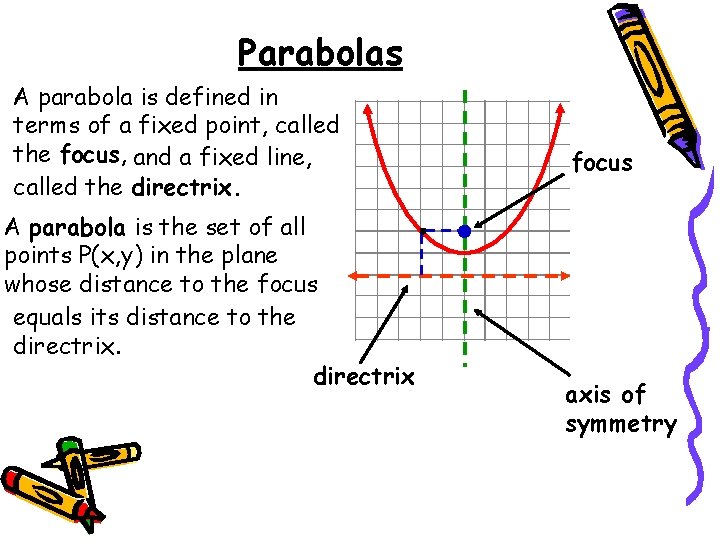
Parabolas A parabola is defined in terms of a fixed point, called the focus, and a fixed line, called the directrix. A parabola is the set of all points P(x, y) in the plane whose distance to the focus equals its distance to the directrix focus axis of symmetry

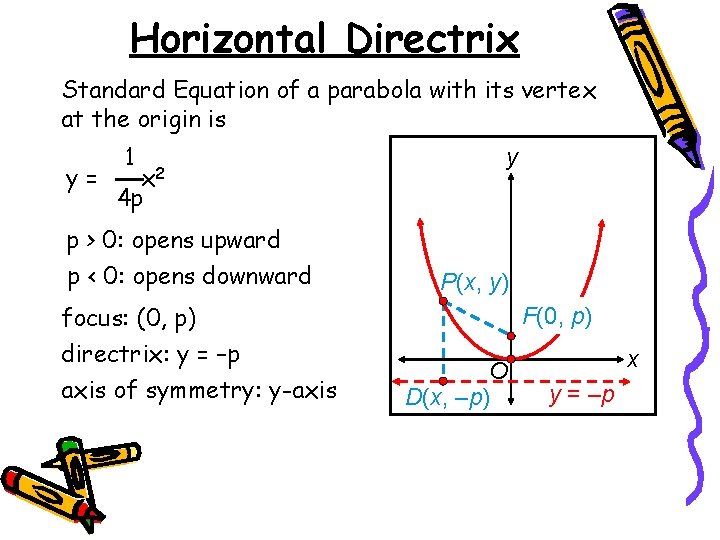
Horizontal Directrix Standard Equation of a parabola with its vertex at the origin is y= 1 x 2 y 4 p p > 0: opens upward p < 0: opens downward focus: (0, p) directrix: y = –p axis of symmetry: y-axis P(x, y) F(0, p) O D(x, –p) x y = –p

Vertical Directrix Standard Equation of a parabola with its vertex at the origin is x= 1 4 p y 2 p > 0: opens right y D(x, –p) P(x, y) p < 0: opens left focus: (p, 0) directrix: x = –p axis of symmetry: x-axis O x = –p F(p, 0) x

Example 1 Graph directrix. . Label the vertex, focus, and Identify p. 4 So, p = 1 Since p > 0, the parabola opens to the right. Vertex: (0, 0) Focus: (1, 0) Directrix: x = -1 2 -4 -2 -2 -4 2 4

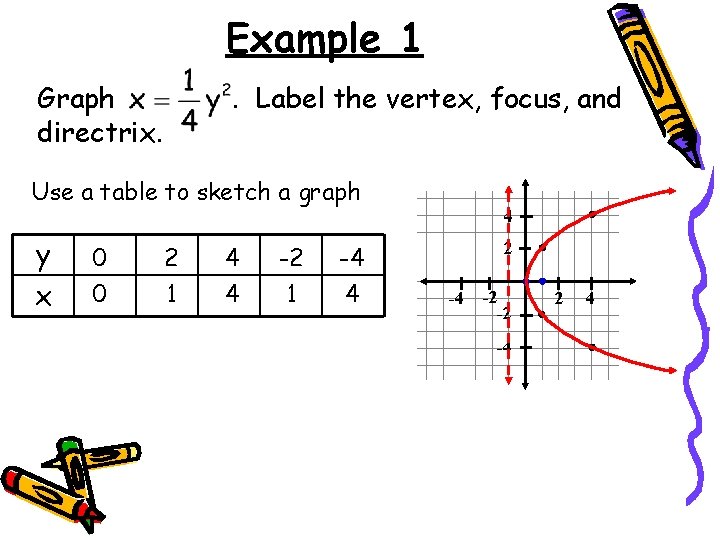
Example 1 Graph directrix. . Label the vertex, focus, and Use a table to sketch a graph y x 0 2 4 -2 -4 0 1 4 4 2 -4 -2 -2 -4 2 4

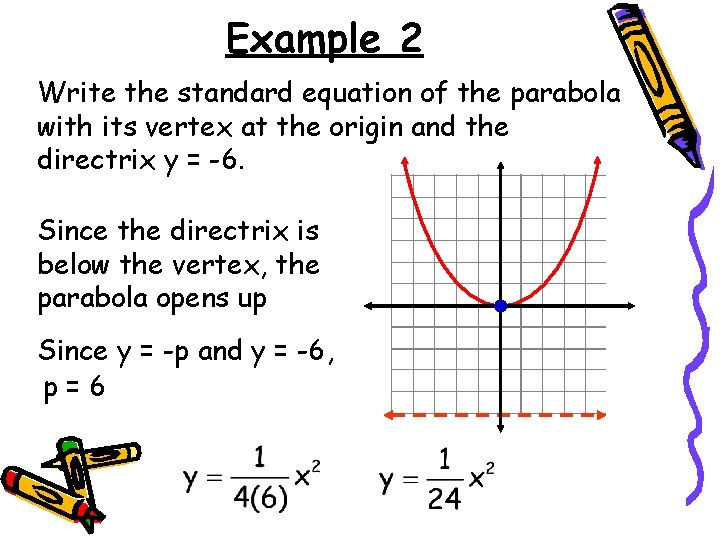
Example 2 Write the standard equation of the parabola with its vertex at the origin and the directrix y = -6. Since the directrix is below the vertex, the parabola opens up Since y = -p and y = -6, p=6

Standard Equation of a Translated Parabola Horizontal Directrix: 1 y–k= (x – h)2 4 p vertex: (h, k) focus: (h, k + p) directrix: y = k – p axis of symmetry: x = h

Standard Equation of a Translated Parabola Vertical Directrix: 1 x–h= (y - k)2 4 p vertex: (h, k) focus: (h + p, k) directrix: x = h - p axis of symmetry: y = k

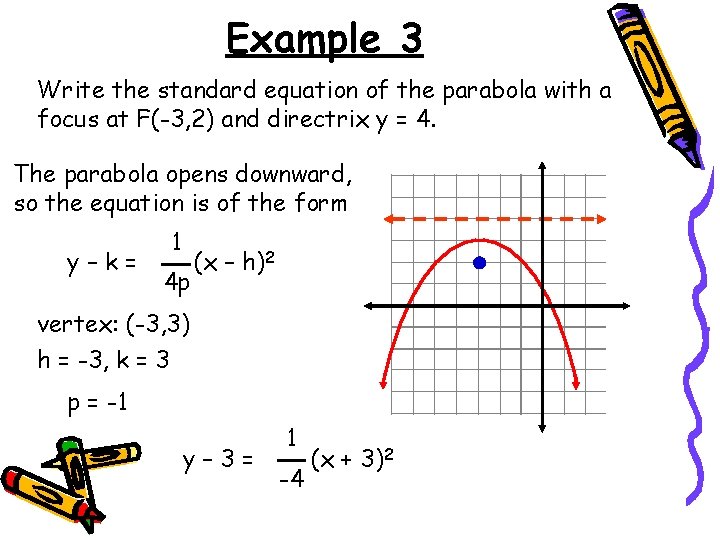
Example 3 Write the standard equation of the parabola with a focus at F(-3, 2) and directrix y = 4. The parabola opens downward, so the equation is of the form y–k= 1 4 p (x – h)2 vertex: (-3, 3) h = -3, k = 3 p = -1 y– 3= 1 -4 (x + 3)2

Example 4 Graph the parabola . Label the vertex, focus, and directrix. -4( ) ( )-4 Isolate the y-terms Complete the square

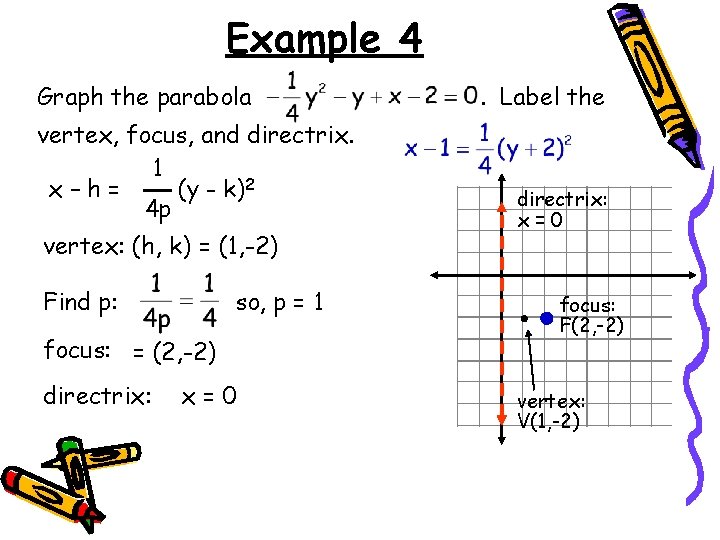
Example 4 Graph the parabola vertex, focus, and directrix. 1 x–h= (y - k)2 4 p vertex: (h, k) = (1, -2) Find p: so, p = 1 focus: = (2, -2) directrix: x=0 . Label the directrix: x=0 focus: F(2, -2) vertex: V(1, -2)

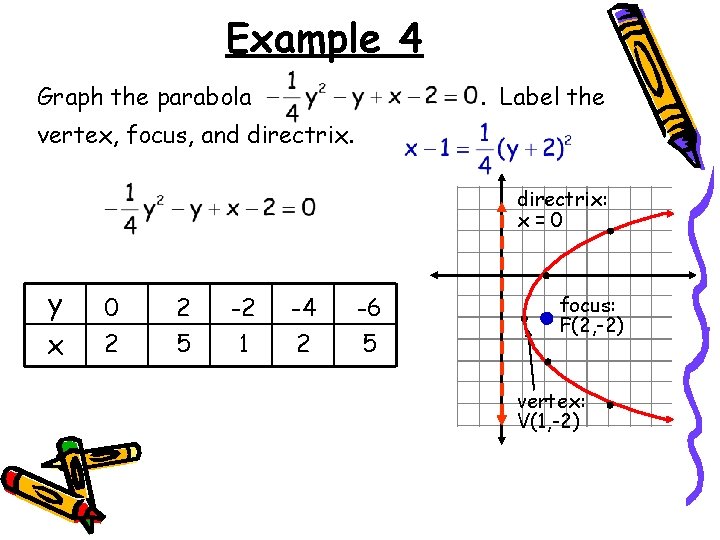
Example 4 Graph the parabola . Label the vertex, focus, and directrix: x=0 y x 0 2 2 5 -2 1 -4 2 -6 5 focus: F(2, -2) vertex: V(1, -2)

Homeworksheet