6 Inverse Circular Functions and Trigonometric Equations Copyright

































- Slides: 38

6 Inverse Circular Functions and Trigonometric Equations Copyright © 2013, 2009, 2005 Pearson Education, Inc. 1

6 Inverse Circular Functions and Trigonometric Equations 6. 1 Inverse Circular Functions 6. 2 Trigonometric Equations I 6. 3 Trigonometric Equations II Copyright © 2013, 2009, 2005 Pearson Education, Inc. 2

6. 1 Inverse Circular Functions Inverse Functions ▪ Inverse Sine Function ▪ Inverse Cosine Function ▪ Inverse Tangent Function ▪ Remaining Inverse Circular Functions ▪ Inverse Function Values Copyright © 2013, 2009, 2005 Pearson Education, Inc. 3

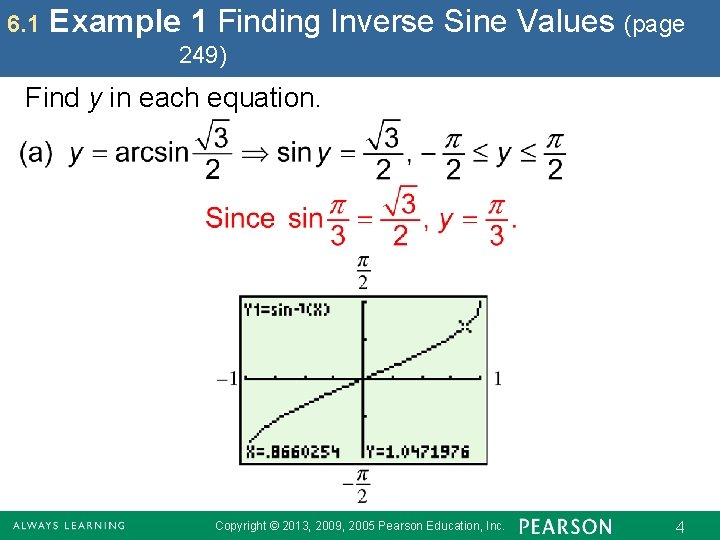
6. 1 Example 1 Finding Inverse Sine Values (page 249) Find y in each equation. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 4

6. 1 Example 1 Finding Inverse Sine Values (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 5

6. 1 Example 1 Finding Inverse Sine Values (cont. ) is not in the domain of the inverse sine function, [– 1, 1], so does not exist. A graphing calculator will give an error message for this input. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6

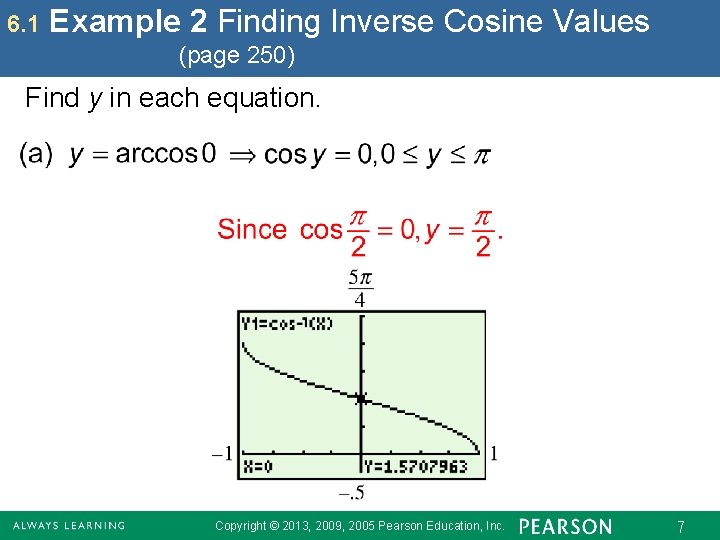
6. 1 Example 2 Finding Inverse Cosine Values (page 250) Find y in each equation. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 7

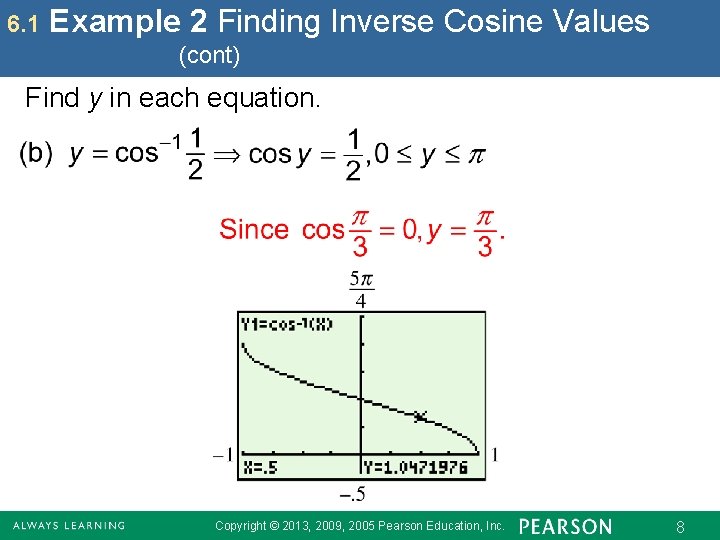
6. 1 Example 2 Finding Inverse Cosine Values (cont) Find y in each equation. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 8

6. 1 Example 3 Finding Inverse Function Values (Degree-Measured Angles) (page 253) Find the degree measure of θ in each of the following. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 9

6. 1 Example 4 Finding Inverse Function Values With a Calculator (page 254) (a) Find y in radians if With the calculator in radian mode, enter as y = 1. 823476582 Copyright © 2013, 2009, 2005 Pearson Education, Inc. 10

6. 1 Example 4(b) Finding Inverse Function Values With a Calculator (page 254) (b) Find θ in degrees if θ = arccot(– 0. 2528). A calculator gives the inverse cotangent value of a negative number as a quadrant IV angle. The restriction on the range of arccotangent implies that the angle must be in quadrant II, so, with the calculator in degree mode, enter arccot(– 0. 2528) as Copyright © 2013, 2009, 2005 Pearson Education, Inc. 11

6. 1 Example 4(b) Finding Inverse Function Values With a Calculator (cont. ) θ = 104. 1871349° Copyright © 2013, 2009, 2005 Pearson Education, Inc. 12

6. 1 Example 5 Finding Function Values Using Definitions of the Trigonometric Functions (page 254) Evaluate each expression without a calculator. Since arcsin is defined only in quadrants I and IV, and is positive, θ is in quadrant I. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 13

6. 1 Example 5(a) Finding Function Values Using Definitions of the Trigonometric Functions (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 14

6. 1 Example 5(b) Finding Function Values Using Definitions of the Trigonometric Functions (page 266) Since arccot is defined only in quadrants I and II, and is negative, θ is in quadrant II. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 15

6. 1 Example 5(b) Finding Function Values Using Definitions of the Trigonometric Functions (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 16

6. 1 Example 6(a) Finding Function Values Using Identities (page 255) Evaluate the expression without a calculator. Use the cosine difference identity: Copyright © 2013, 2009, 2005 Pearson Education, Inc. 17

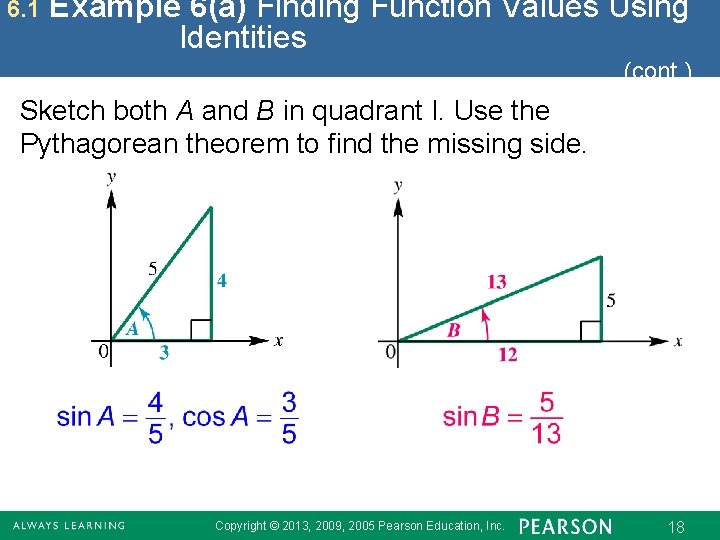
6. 1 Example 6(a) Finding Function Values Using Identities (cont. ) Sketch both A and B in quadrant I. Use the Pythagorean theorem to find the missing side. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 18

6. 1 Example 6(a) Finding Function Values Using Identities (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 19

6. 1 Example 6(b) Finding Function Values Using Identities (page 255) Evaluate the expression without a calculator. sin(2 arccot (– 5)) Let A = arccot (– 5), so cot A = – 5. Use the double-angle sine identity: Copyright © 2013, 2009, 2005 Pearson Education, Inc. 20

6. 1 Example 6(b) Finding Function Values Using Identities (cont. ) Sketch A in quadrant II. Use the Pythagorean theorem to find the missing side. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 21

6. 1 Example 6(b) Finding Function Values Using Identities (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 22

6. 1 Example 7(a) Finding Function Values in Terms of u (page 256) Write in u. , as an algebraic expression Sketch θ in quadrant I. Use the Pythagorean theorem to find the missing side. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 23

6. 1 Example 7(a) Finding Function Values in Terms of u (cont. ) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 24

6. 1 Example 7(b) Finding Function Values in Terms of u (page 256) Write in u. , u > 0, as an algebraic expression Sketch θ in quadrant I. Use the Pythagorean theorem to find the missing side. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 25

6. 1 Example 7(b) Finding Function Values in Terms of u (cont. ) Use the double-angle sine identity to find sin 2θ. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 26

6. 2 Trigonometric Equations I Solving by Linear Methods ▪ Solving by Factoring ▪ Solving by Quadratic Methods ▪ Solving by Using Trigonometric Identities Copyright © 2013, 2009, 2005 Pearson Education, Inc. 27

6. 2 Example 1 a Solving a Trigonometric Equation by Linear Methods (page 262) is positive in quadrants I and III. The reference angle is 30° because Copyright © 2013, 2009, 2005 Pearson Education, Inc. 6 -28 28

6. 2 Example 1 Solving a Trigonometric Equation by Linear Methods (cont. ) Solution set: {30°, 210°} b) for all solutions Solution set: {30° + 180°n, where n is any integer} Copyright © 2013, 2009, 2005 Pearson Education, Inc. 29

6. 2 Example 2 Solving a Trigonometric Equation by Factoring (page 263) or Solution set: {90°, 135°, 270°, 315°} Copyright © 2013, 2009, 2005 Pearson Education, Inc. 30

6. 2 Example 3 Solving a Trigonometric Equation by Factoring (page 263) Copyright © 2013, 2009, 2005 Pearson Education, Inc. 31

6. 2 Example 3 Solving a Trigonometric Equation by Factoring (cont. ) has two solutions, the angles in quadrants III and IV with the reference angle. 729728: 3. 8713 and 5. 5535. has one solution, Copyright © 2013, 2009, 2005 Pearson Education, Inc. 32

6. 3 Trigonometric Equations II Equations with Half-Angles ▪ Equations with Multiple Angles Copyright © 2013, 2009, 2005 Pearson Education, Inc. 33

6. 3 Example 1 Solving an Equation Using a Half. Angle Identity (page 269) (a) over the interval and (b) give all solutions. is not in the requested domain. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 34

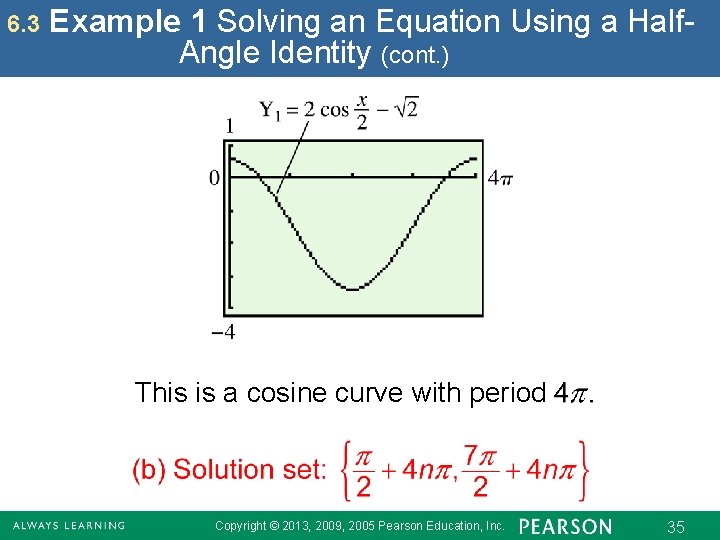
6. 3 Example 1 Solving an Equation Using a Half. Angle Identity (cont. ) This is a cosine curve with period Copyright © 2013, 2009, 2005 Pearson Education, Inc. 35

6. 3 Example 2 Solving an Equation With a Double Angle (page 270) Factor. or Copyright © 2013, 2009, 2005 Pearson Education, Inc. 36

6. 3 Example 3 Solving an Equation Using a Multiple Angle Identity (page 270) From the given interval 0° ≤ θ < 360°, the interval for 2θ is 0° ≤ 2θ < 720°. Copyright © 2013, 2009, 2005 Pearson Education, Inc. 37

6. 3 Example 3 Solving an Equation Using a Multiple Angle Identity (cont. ) Since cosine is negative in quadrants II and III, solutions over this interval are Copyright © 2013, 2009, 2005 Pearson Education, Inc. 38