6 Implementation of VectorSpace Retrieval These notes are

6. Implementation of Vector-Space Retrieval These notes are based, in part, on notes by Dr. Raymond J. Mooney at the University of Texas at Austin. 1

Vector Space Retrieval (Naïve version) Steps: 1. Convert all documents in collection D to tf-idf weighted vectors, dj, for term vocabulary V. 2. Convert query to a tf-idf-weighted vector q. 3. For each dj in D do Compute score sj = cos. Sim(dj, q) 4. Sort documents by decreasing score. 5. Present top ranked documents to the user. Time complexity: O(|V|·|D|) Bad for large V & D ! |V| = 10, 000; |D| = 100, 000; |V|·|D| = 1, 000, 000 2

Implementation Based on Inverted Files • In practice, document vectors are not stored directly; an inverted list provides much better efficiency. • The dictionary part can be implemented as a hash table, a sorted array, or a tree-based data structure (trie, B-tree). • Critical issue is logarithmic or constant-time access to token information. 3

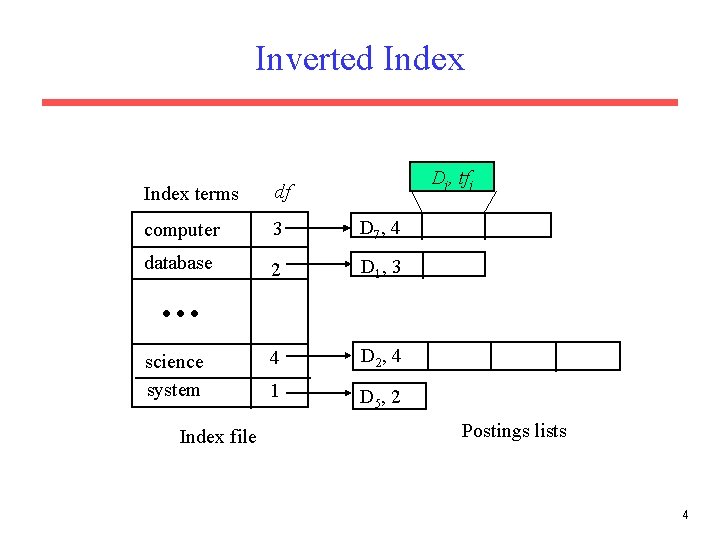
Inverted Index Dj, tfj Index terms df computer 3 D 7 , 4 database 2 D 1 , 3 4 D 2 , 4 1 D 5 , 2 science system Index file Postings lists 4

Step 1: Indexing Documents Skipping the algorithm, these data structures store indices. • Assume a dictionary (for all terms in the vocabulary) is stored in a Hash. Map, which maps a term to its inverse document frequencies (IDF) – called ‘H’ in the algo. • Assume a posting list (term frequency information) is stored in a vector of Hash. Map’s, which maps a document. ID to the (raw) TF of the term in the document. 5

Note on Document Length • We also compute document length (for all documents) and store them in a Hash. Map , which maps a document. ID to the length – called ‘DL’ in the algo. • Remember that the length of a document vector is the square-root of sum of the squares of the weights of its tokens – and the weight of a token is TF * IDF. • Therefore, must wait until IDF’s are known (and therefore until all documents are indexed) before document lengths can be determined. 6

Retrieval with an Inverted Index • Tokens that are not in both the query and the document do not effect cosine similarity. – Product of token weights is zero and does not contribute to the dot product. • Usually the query is fairly short, and therefore its vector is extremely sparse. • Use inverted index to find the limited set of documents that contain at least one of the query words. 7

Inverted Query Retrieval Efficiency • Assume that, on average, a query word appears in B documents: Q = q 1 D 11…D 1 B q 2 … D 21…D 2 B qn Dn 1…Dn. B • Then retrieval time is O(|Q| B), which is typically, much better than naïve retrieval that examines all N documents, O(|V| N), because |Q| << |V| and B << N. 8

Step 2: Query as a Vector • Create a Hash. Map. Vector, Q, for the query -- a vector of Hash. Map’s, where each term in the query is a Hash. Map that maps a term to its TF in the query. 9

Step 3: Compute Cosine • Incrementally compute cosine similarity of each indexed document as query terms are processed one by one. • To accumulate a total score for each retrieved document, store retrieved documents in a Hash. Map (called ‘R’ in the algo), which maps document. ID’s to computed cosine scores. 10

Inverted-Index Retrieval Algorithm Create empty Hash. Map, R, to store retrieved documents with scores. For each token, T, in Q: Let I be the IDF of T, and K be the frequency of T in Q; Set the weight of T in Q: W = K * I; (tf*idf for T in Q) Let L be the posting list of T from H; For each pair Hash. Map, O, in L: Let D be the document of O, and C be the freq of O (tf of T in D); If D is not already in R (D was not previously retrieved) Then add D to R and initialize score to 0. 0; Increment D’s score by W * C * I; (tf*idf for T in Q x tf*idf for T in D) 11

Inverted-Index Retrieval Algorithm (cont. ) Compute the length, L, of the vector Q (square-root of the sum of the squares of its weights). For each retrieved document D in R: Let S be the current accumulated score of D; (S is the dot-product of D and Q) Let Y be the length of D in DL; Let D’s final score to be S/(L * Y); (the cosine) 12

Step 4 and 5 Sort retrieved documents in R by final score. Return the sorted documents in an array. (ranked results) 13

Exercise Apply the Inverted-Index Retrieval Algorithm to the following, and show the ranked results with cosine values to the query “best car insurance”. 14