6 Friction 1 Objectives Students must be able

6 Friction 1

Objectives Students must be able to • Utilize theory of dry friction – Describe physical meanings of frictional effects – Describe and differentiate between static and kinetic coefficients of friction – Describe the angles of frictions – Add friction into the analyses of objects and structures in equilibrium 2

Objectives Students must be able to • Describe and analyze machines with frictions – Wedges – Threads, screws – Belts – Disks and clutches – Collar, pivot, thrust and journal bearings • Outline rolling resistance – Describe the physical meanings of rolling resistance – Differentiate between frictions and rolling resistance 3

Topic in textbook • Section A: Frictional Phenomena – Characteristics, theory, coefficient of friction, angle of friction • Section B: Applications – Wedges – Screws – Journal Bearings – Thrust Bearings; Disk friction – Flexible Belts – Rolling Resistance We will study this Part first. 4

Dry Friction Force of resistance acting on a body which prevents or retards slipping of the body relative to a surface with which it is in contact. Friction exists? roughnesses of the contacting surfaces. Magnitude: friction’s magnitude limitation will be discussed later Direction: tangent to the contacting surface and opposed to the relative motion or tendency for motion Line of Action (Point of application): contact surface 5

Equilibrium Friction Model y W In equilibrium FBD is correct? a/2 x P modeling h F The DN at right side is supporting force more than its left side. x N If x > a/2 ? • Frictional force F • The application point (x) of N increases with force P Slipping and/or Tipping Effect N The object is toppling (not in equilibrium) toppling Slipping x-limit F-limit 6

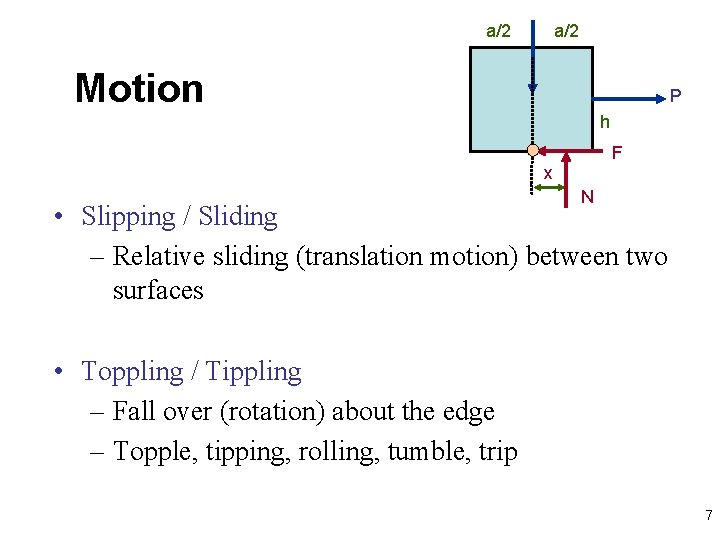
a/2 Motion P h F x N N • Slipping / Sliding – Relative sliding (translation motion) between two surfaces • Toppling / Tippling – Fall over (rotation) about the edge – Topple, tipping, rolling, tumble, trip 7

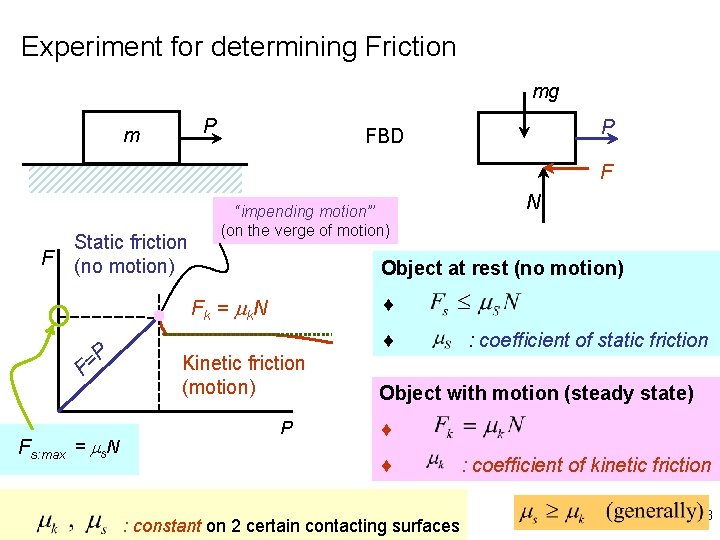
Experiment for determining Friction mg P m P FBD F F Static friction (no motion) “impending motion”’ (on the verge of motion) Object at rest (no motion) ¨ F k = k N P = F Fs: max = s. N N ¨ Kinetic friction (motion) P : coefficient of static friction Object with motion (steady state) ¨ ¨ : constant on 2 certain contacting surfaces : coefficient of kinetic friction 8

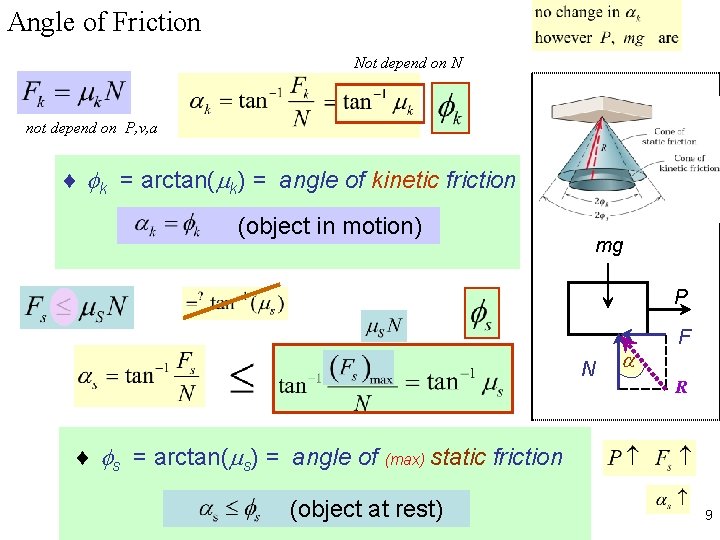
Angle of Friction Not depend on N not depend on P, v, a ¨ k = arctan( k) = angle of kinetic friction (object in motion) mg P N F R ¨ s = arctan( s) = angle of (max) static friction (object at rest) 9

Dry Friction Characteristics • Frictional force acts tangentially to the contacting surfaces, opposing the relative or tendency for motion. • Fs is independent of the area of contact, provided that the normal pressure is not very low nor great enough for deformation of the surfaces. • In equilibrium: Impending slipping: Slipping: Very low velocity: = s = k k » s 10

Dry Friction Impending Motion Static Friction Typical Values Contact Materials Metal / Wood / Leather / Aluminum / ice wood metal Aluminum μs 0. 03 – 0. 05 0. 30 – 0. 70 0. 20 – 0. 50 0. 30 – 0. 60 1. 10 – 1. 70 11

Sample 6/1 Determine the maximum angle which the adjustable incline may have before the block of mass m begins to slip. The coefficient of static friction between the block and the inclined surface is s. W=mg y x H/2 x F “Impending Slip”: N (for slipping) Three force member Ans Possibility of toppling? W=mg 3 eq. , 3 unknowns 12

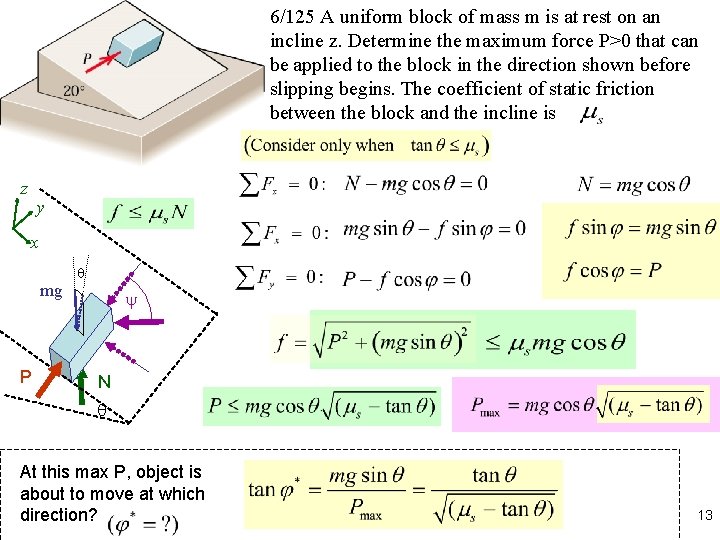
6/125 A uniform block of mass m is at rest on an incline z. Determine the maximum force P>0 that can be applied to the block in the direction shown before slipping begins. The coefficient of static friction between the block and the incline is z y x mg P q y N q At this max P, object is about to move at which direction? 13

Dry Friction Example Friction 2 #1 Will this crate slide or topple over? 14

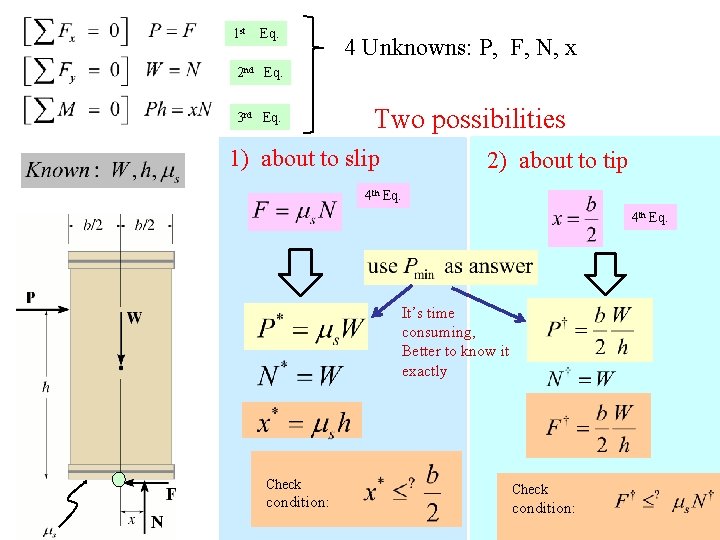
1 st Eq. 4 Unknowns: P, F, N, x 2 nd Eq. 3 rd Eq. Two possibilities 1) about to slip 2) about to tip 4 th Eq. It’s time consuming, Better to know it exactly Check condition:

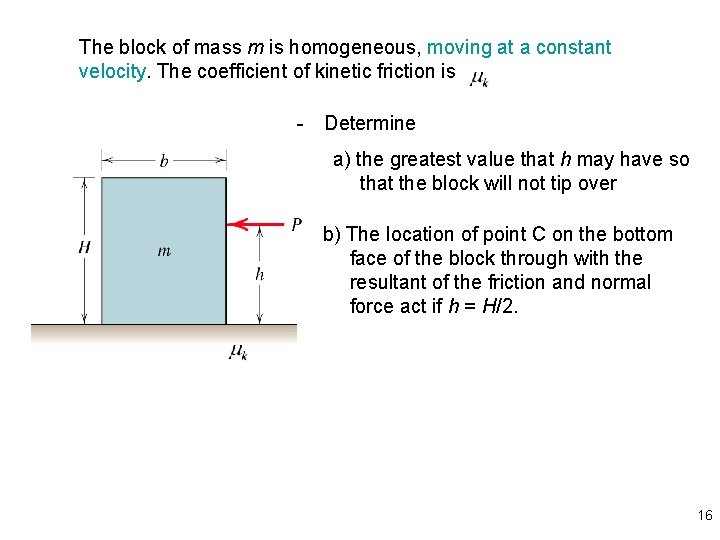
The block of mass m is homogeneous, moving at a constant velocity. The coefficient of kinetic friction is - Determine a) the greatest value that h may have so that the block will not tip over b) The location of point C on the bottom face of the block through with the resultant of the friction and normal force act if h = H/2. 16

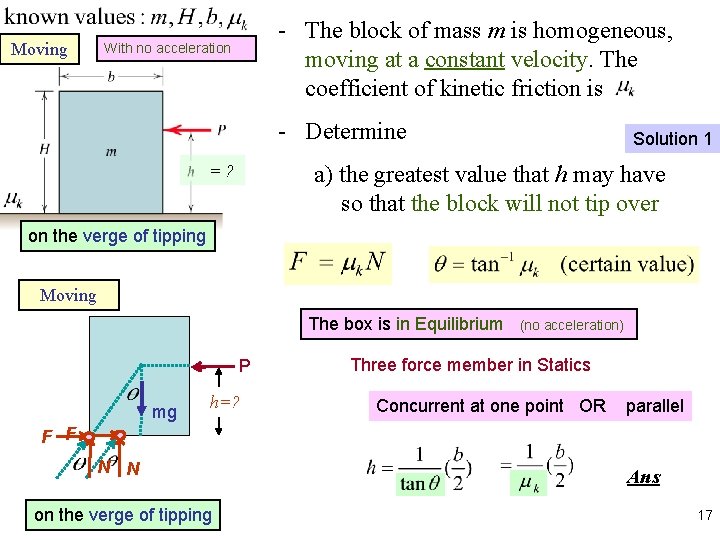
Moving - The block of mass m is homogeneous, moving at a constant velocity. The coefficient of kinetic friction is With no acceleration - Determine Solution 1 a) the greatest value that h may have so that the block will not tip over =? on the verge of tipping Moving The box is in Equilibrium P mg h=? (no acceleration) Three force member in Statics Concurrent at one point OR parallel F F N N on the verge of tipping Ans 17

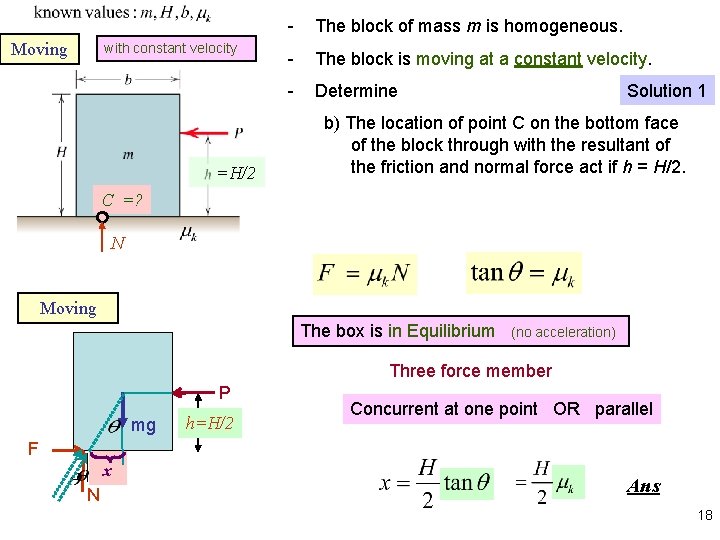
Moving with constant velocity =H/2 - The block of mass m is homogeneous. - The block is moving at a constant velocity. - Determine Solution 1 b) The location of point C on the bottom face of the block through with the resultant of the friction and normal force act if h = H/2. C =? N Moving The box is in Equilibrium (no acceleration) Three force member P mg h=H/2 Concurrent at one point OR parallel F x N Ans 18

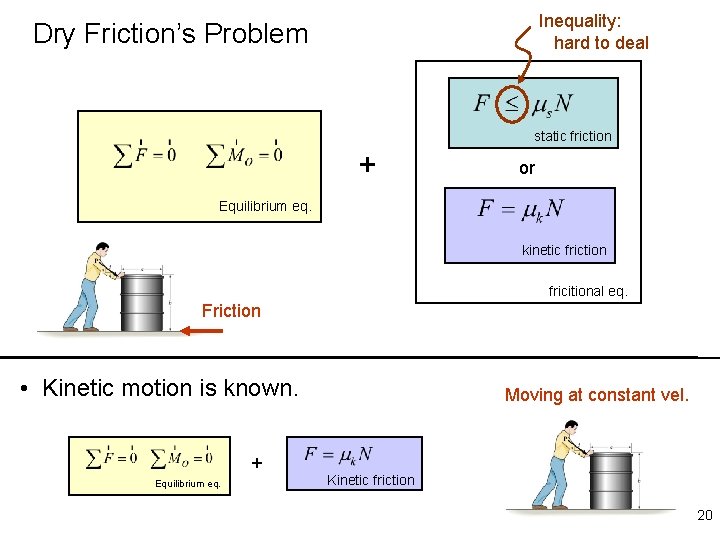
Inequality: hard to deal Dry Friction’s Problem static friction + or Equilibrium eq. kinetic friction fricitional eq. Friction • Kinetic motion is known. + Equilibrium eq. Moving at constant vel. Kinetic friction 20

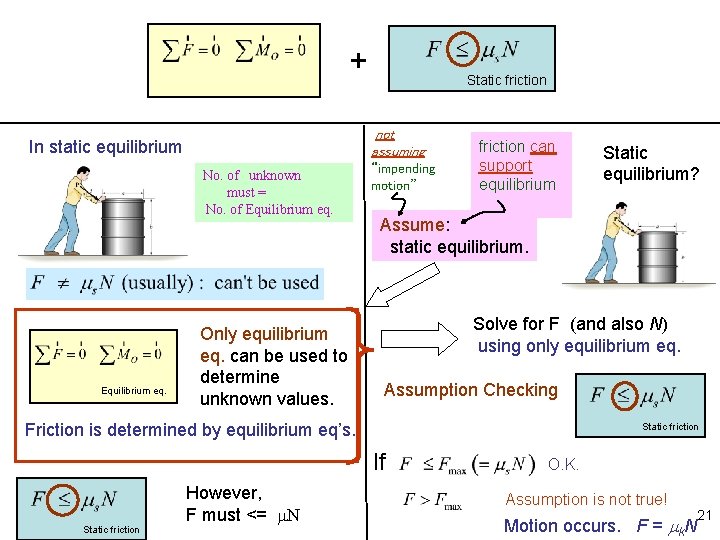
+ not assuming In static equilibrium No. of unknown must = No. of Equilibrium eq. Static friction Only equilibrium eq. can be used to determine unknown values. “impending motion” friction can support equilibrium Assume: static equilibrium. Solve for F (and also N) using only equilibrium eq. Assumption Checking Friction is determined by equilibrium eq’s. Static friction If Static friction However, F must <= m. N Static equilibrium? O. K. Assumption is not true! Motion occurs. F = k. N 21

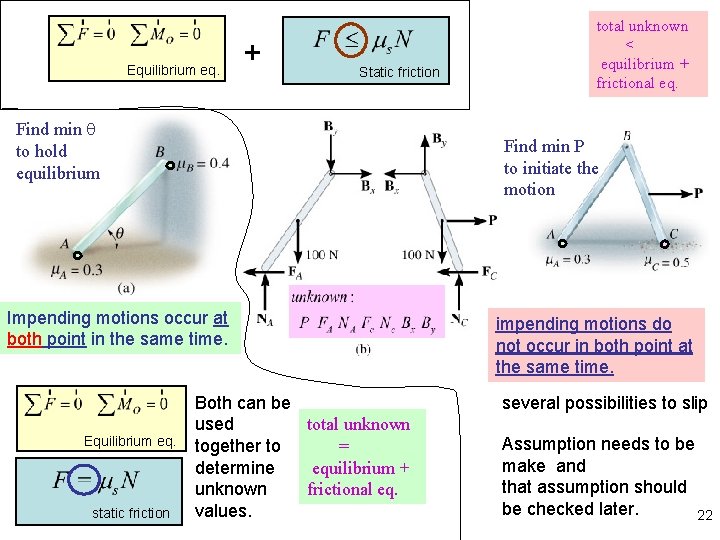
Equilibrium eq. + Static friction Find min q to hold equilibrium Find min P to initiate the motion Impending motions occur at both point in the same time. Equilibrium eq. static friction total unknown < equilibrium + frictional eq. Both can be used total unknown together to = determine equilibrium + unknown frictional eq. values. impending motions do not occur in both point at the same time. several possibilities to slip Assumption needs to be make and that assumption should be checked later. 22

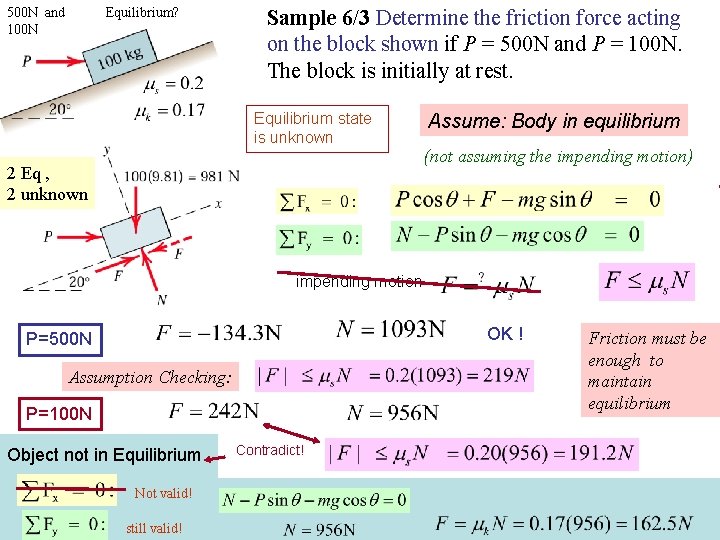
500 N and 100 N Equilibrium? Sample 6/3 Determine the friction force acting on the block shown if P = 500 N and P = 100 N. The block is initially at rest. Equilibrium state is unknown 2 Eq , 2 unknown Assume: Body in equilibrium (not assuming the impending motion) impending motion OK ! P=500 N Assumption Checking: P=100 N Object not in Equilibrium Friction must be enough to maintain Correct? equilibrium Contradict! Not valid! still valid! 23

Dry Friction Example Hibbeler Ex 8 -1 #1 The uniform crate has a mass of 20 kg. If a force P = 80 N is applied to the crate, determine whether it remains in equilibrium. The coefficient of static friction = 0. 3. Equilibrium State is not known 24

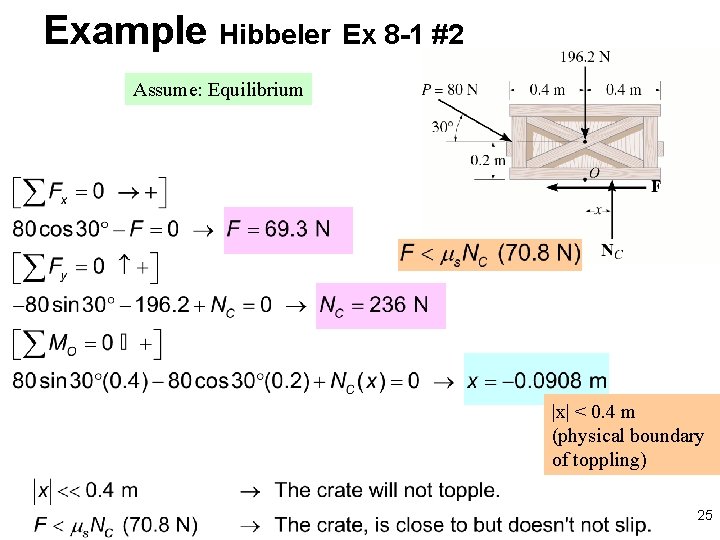
Example Hibbeler Ex 8 -1 #2 Assume: Equilibrium |x| < 0. 4 m (physical boundary of toppling) 25

Dry Friction Example Bedford Ex 9. 5 #1 Suppose that = 10° and the coefficient of friction between the surface of the wedge and the log are s = 0. 22 and k = 0. 20. Neglect the weight of the wedge. – If the wedge is driven into the log at a constant rate by vertical force F, what are the magnitude of the normal forces exerted on the log by the wedge? – Will the wedge remain in place in the log when the force is removed? 26

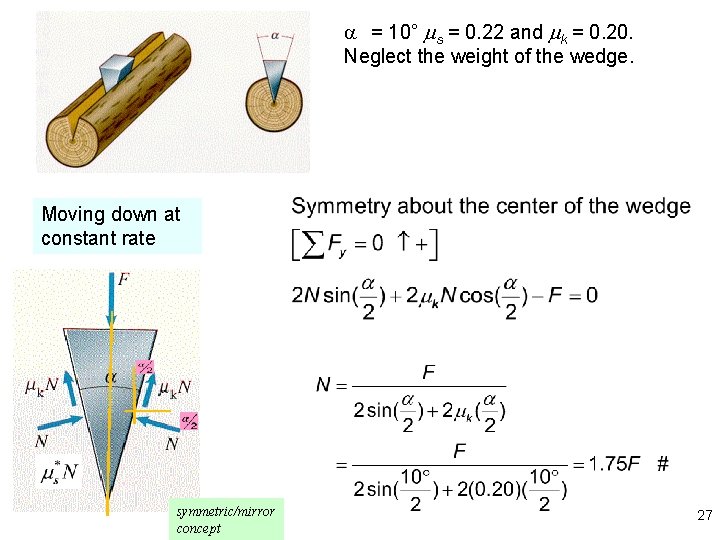
a = 10° s = 0. 22 and k = 0. 20. Neglect the weight of the wedge. Moving down at constant rate symmetric/mirror concept 27

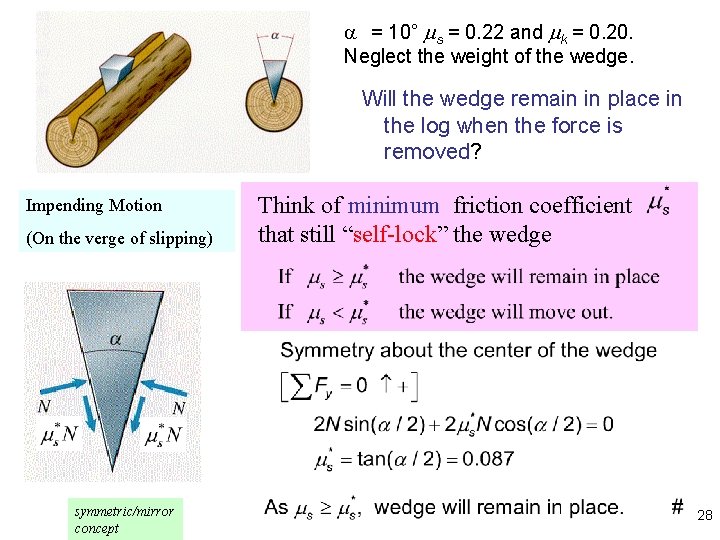
a = 10° s = 0. 22 and k = 0. 20. Neglect the weight of the wedge. Will the wedge remain in place in the log when the force is removed? Impending Motion (On the verge of slipping) symmetric/mirror concept Think of minimum friction coefficient that still “self-lock” the wedge 28

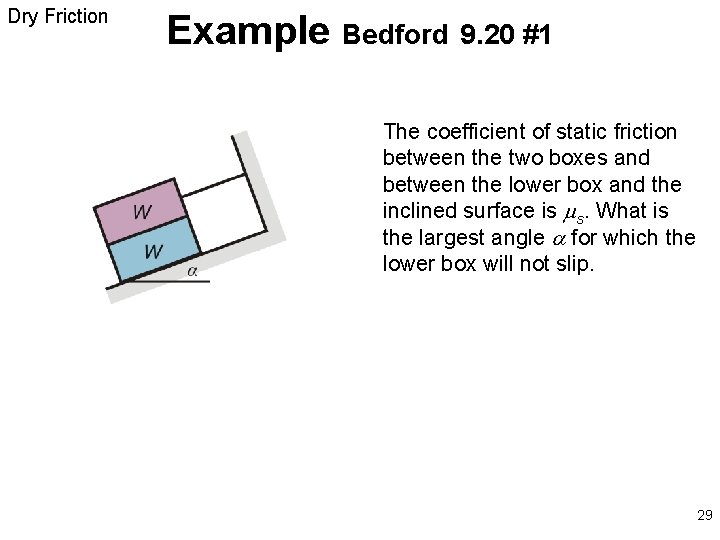
Dry Friction Example Bedford 9. 20 #1 The coefficient of static friction between the two boxes and between the lower box and the inclined surface is s. What is the largest angle for which the lower box will not slip. 29

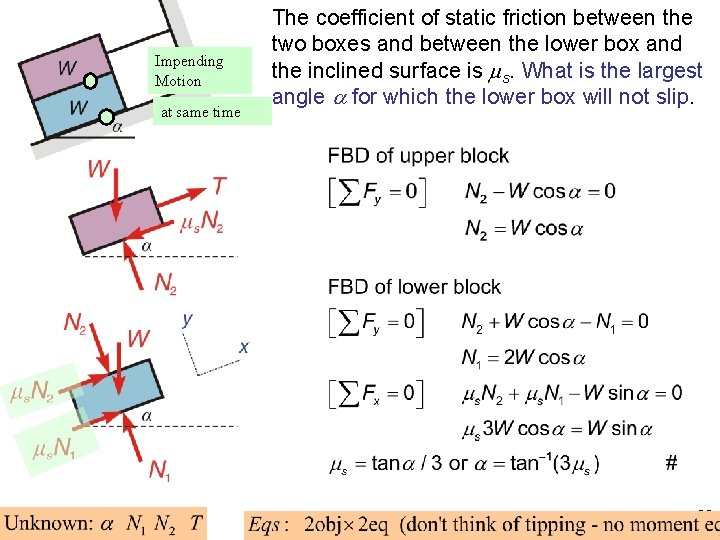
Impending Motion at same time ? The coefficient of static friction between the two boxes and between the lower box and the inclined surface is s. What is the largest angle for which the lower box will not slip. 30

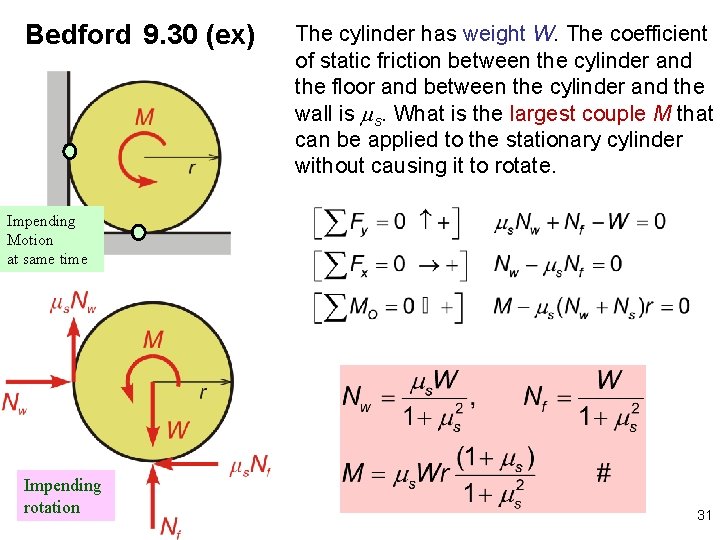
Bedford 9. 30 (ex) The cylinder has weight W. The coefficient of static friction between the cylinder and the floor and between the cylinder and the wall is s. What is the largest couple M that can be applied to the stationary cylinder without causing it to rotate. Impending Motion at same time Impending rotation 31

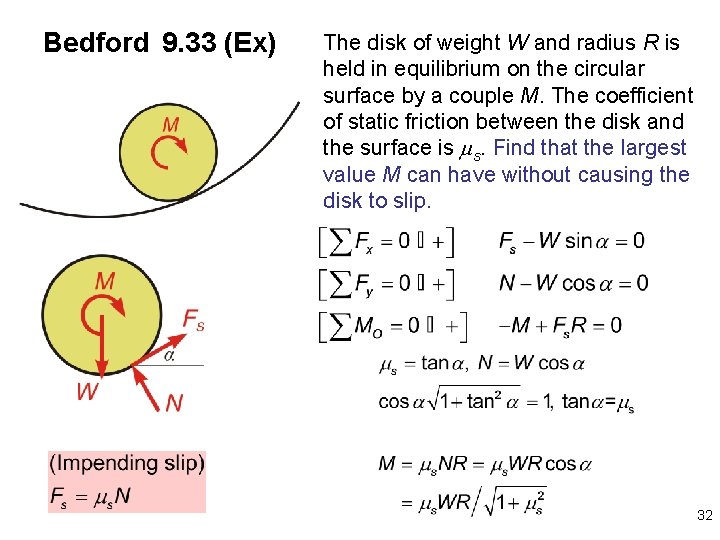
Bedford 9. 33 (Ex) The disk of weight W and radius R is held in equilibrium on the circular surface by a couple M. The coefficient of static friction between the disk and the surface is s. Find that the largest value M can have without causing the disk to slip. 32

Dry Friction Example Bedford 9. 166 #1 Each of the uniform 1 -m bars has a mass of 4 kg. The coefficient of static friction between the bar and the surface at B is 0. 2. If the system is in equilibrium, what is the magnitude of the friction force exerted on the bar at B. 33

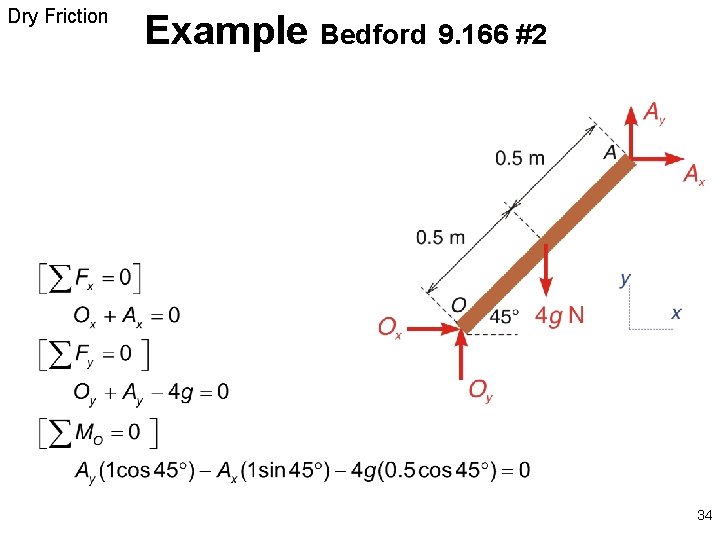
Dry Friction Example Bedford 9. 166 #2 34

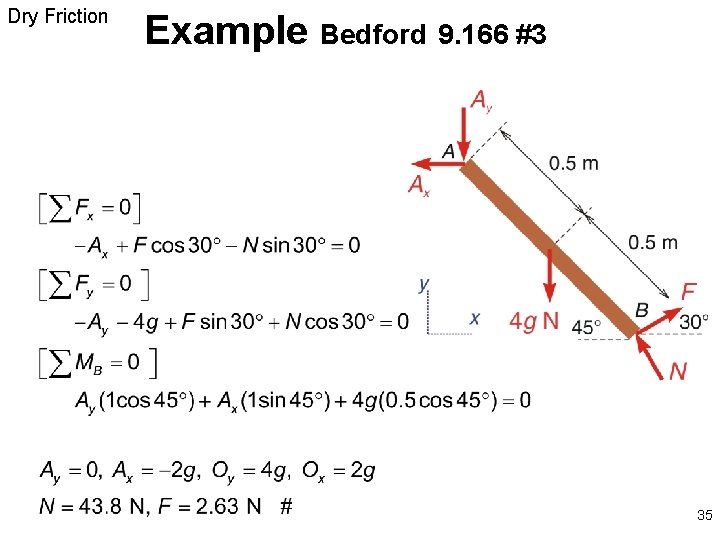
Dry Friction Example Bedford 9. 166 #3 35

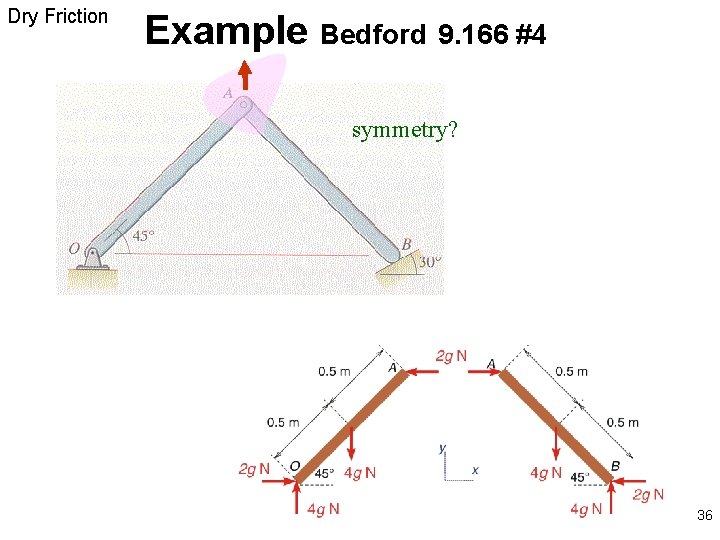
Dry Friction Example Bedford 9. 166 #4 symmetry? 36

Dry Friction Example Hibbeler Ex 8 -3 #1 The rod with weight W is about to slip on rough surfaces at A and B. Find coefficient of static friction. Direction of N? 38

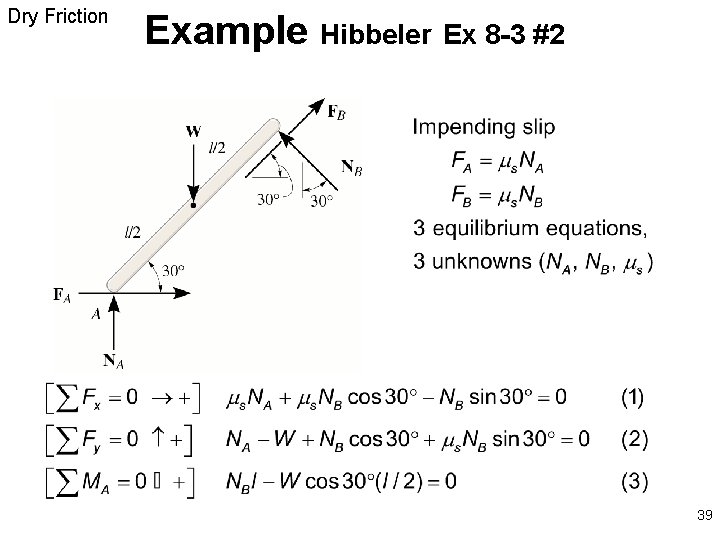
Dry Friction Example Hibbeler Ex 8 -3 #2 39

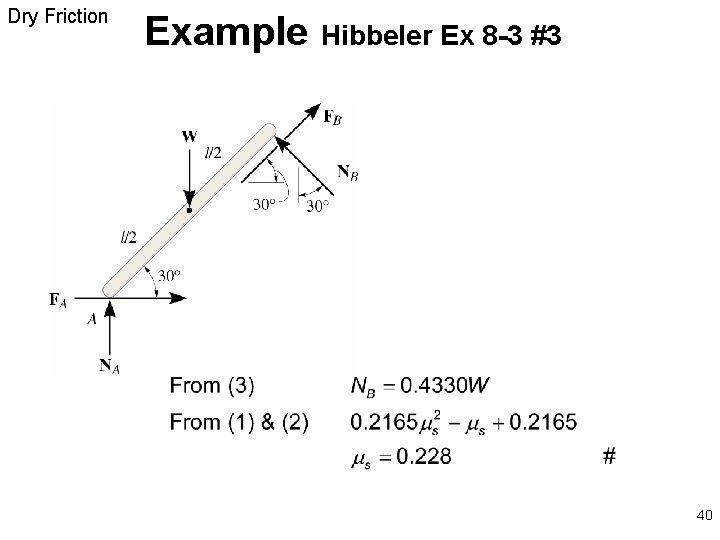
Dry Friction Example Hibbeler Ex 8 -3 #3 40

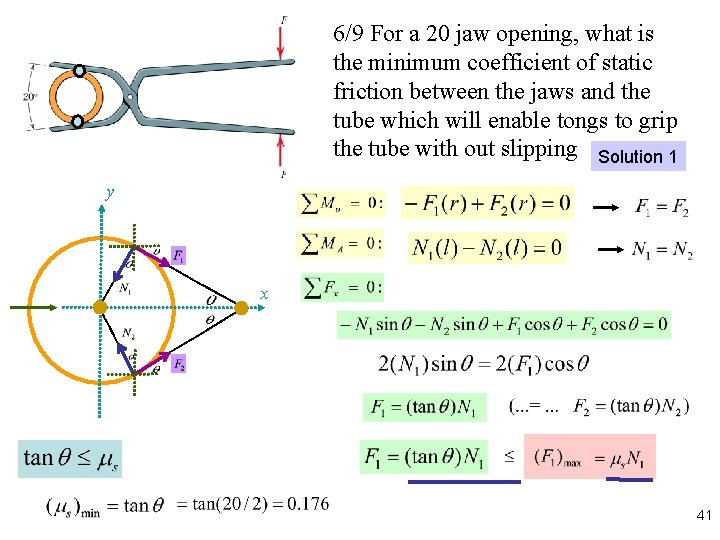
6/9 For a 20 jaw opening, what is the minimum coefficient of static friction between the jaws and the tube which will enable tongs to grip the tube with out slipping Solution 1 y x 41

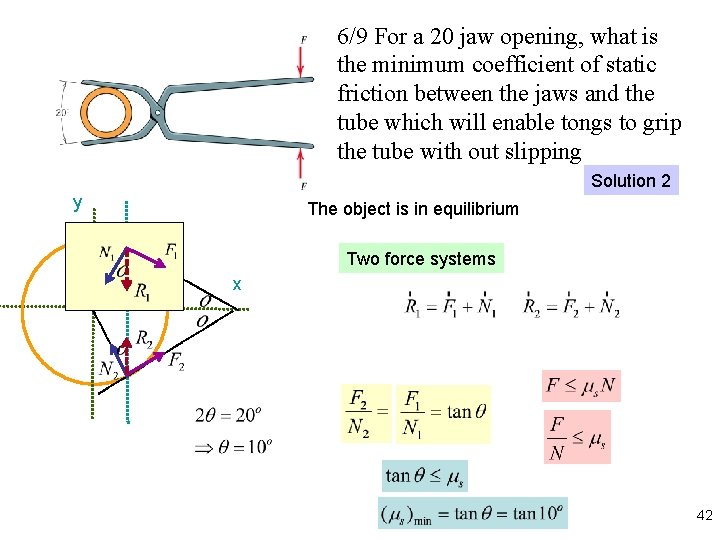
6/9 For a 20 jaw opening, what is the minimum coefficient of static friction between the jaws and the tube which will enable tongs to grip the tube with out slipping Solution 2 y The object is in equilibrium Two force systems x 42

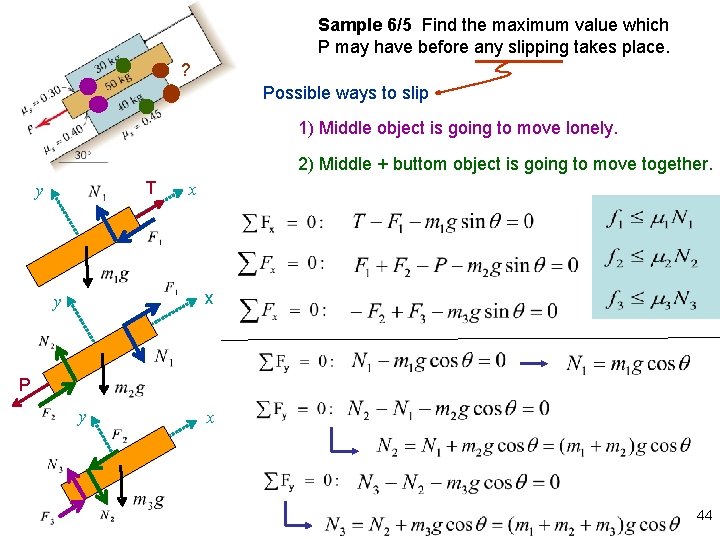
Sample 6/5 Find the maximum value which P may have before any slipping takes place. ? Possible ways to slip 1) Middle object is going to move lonely. 2) Middle + buttom object is going to move together. T y x x y P y x 44

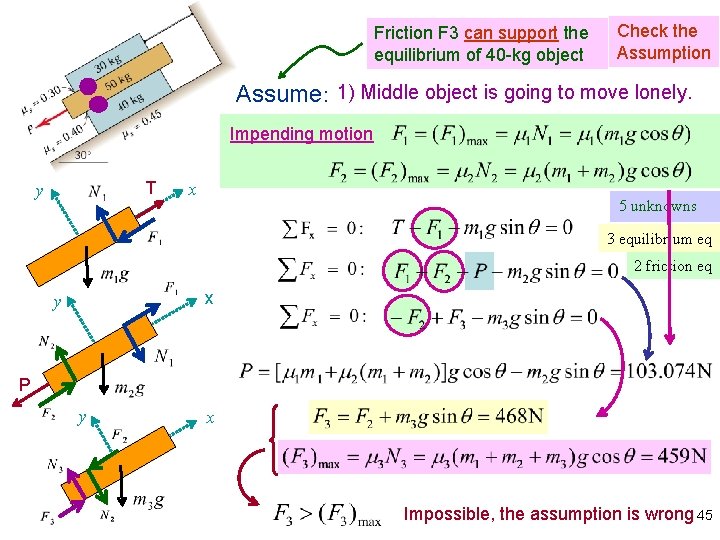
Friction F 3 can support the equilibrium of 40 -kg object Check the Assumption Assume: 1) Middle object is going to move lonely. Impending motion T y x 5 unknowns 3 equilibrium eq 2 friction eq x y P y x Impossible, the assumption is wrong 45

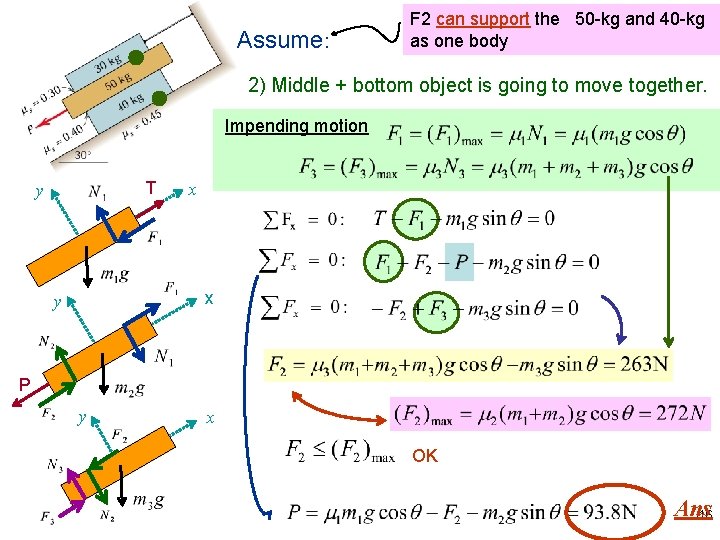
Assume: F 2 can support the 50 -kg and 40 -kg as one body 2) Middle + bottom object is going to move together. Impending motion T y x x y P y x OK Ans 46

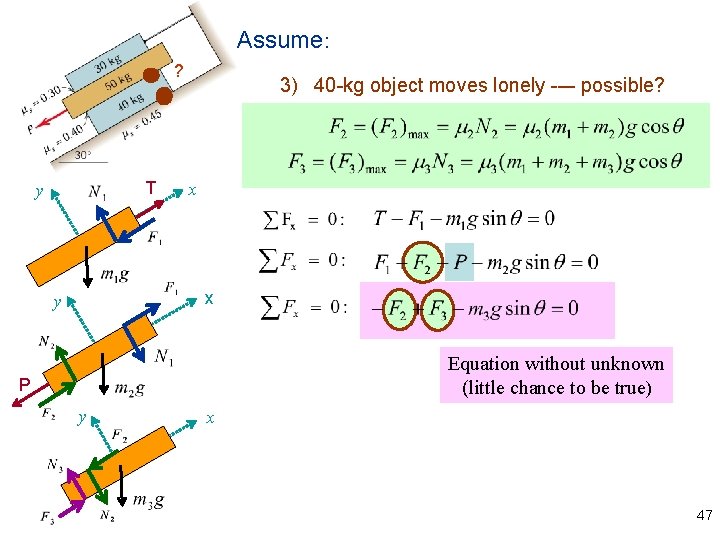
Assume: ? T y 3) 40 -kg object moves lonely --– possible? x x y Equation without unknown (little chance to be true) P y x 47

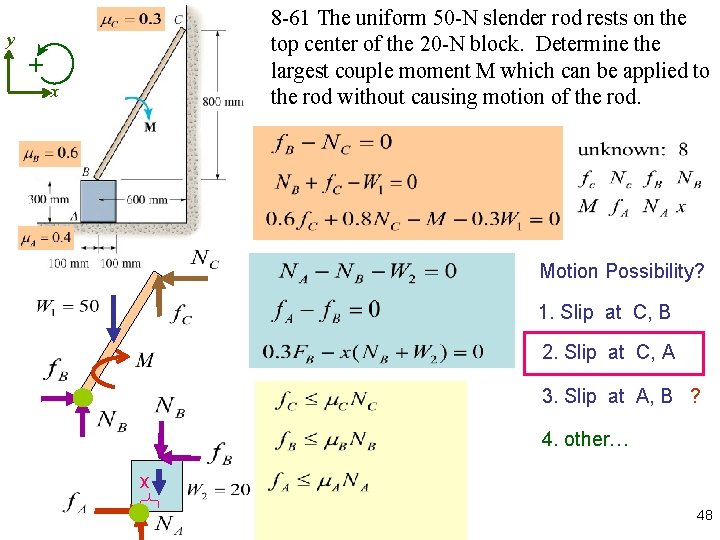
y + 8 -61 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Motion Possibility? 1. Slip at C, B 2. Slip at C, A 3. Slip at A, B ? 4. other… x 48

y + 8 -61 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Assume 2. Slip at C, A 8 unknowns, 6+2 equation. Don’t solve 8 eq paralleling! Solve only 6 eq. excluding Assumption Checking x 49

y + 8 -56 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Assume 2. Slip at C, A Block is tipping = 0. 12 m = 62. 5 N = 9. 5 N-m = 42. 5 N = 25 N = 7. 5 N Assumption Checking Correct? 50

y + 8 -61 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Possibility? 1. Slip at C, B 2. Slip at C, A 3. Slip at A, B ? 4. C-Slip, other…x-limit x 5. B-Slip, x-limit 6. A-Slip, x-limit 51

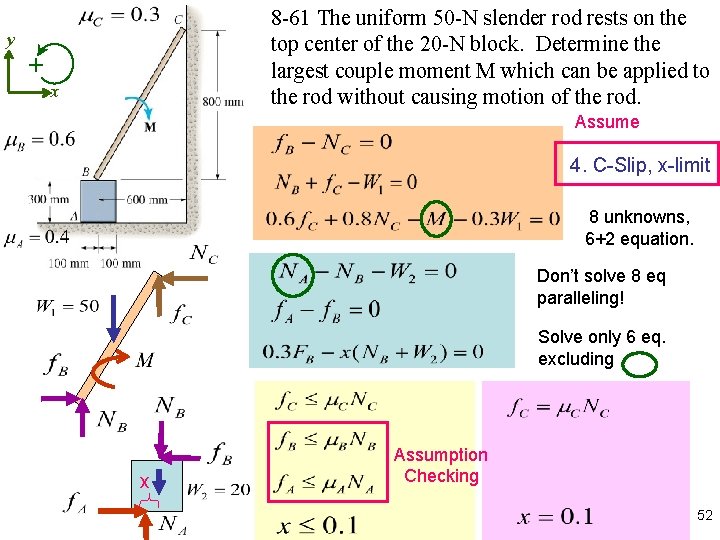
y + 8 -61 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Assume 4. C-Slip, x-limit 8 unknowns, 6+2 equation. Don’t solve 8 eq paralleling! Solve only 6 eq. excluding x Assumption Checking 52

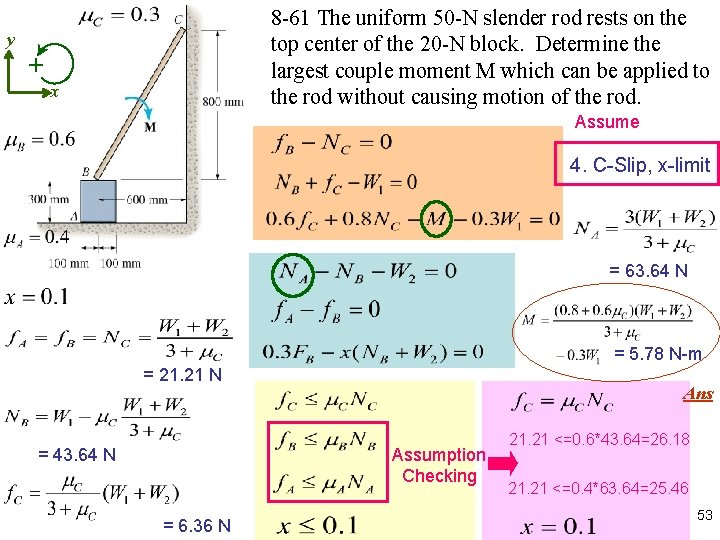
y + 8 -61 The uniform 50 -N slender rod rests on the top center of the 20 -N block. Determine the largest couple moment M which can be applied to the rod without causing motion of the rod. x Assume 4. C-Slip, x-limit = 63. 64 N = 5. 78 N-m = 21. 21 N = 43. 64 N Ans Assumption Checking = 6. 36 N 21. 21 <=0. 6*43. 64=26. 18 21. 21 <=0. 4*63. 64=25. 46 53

54

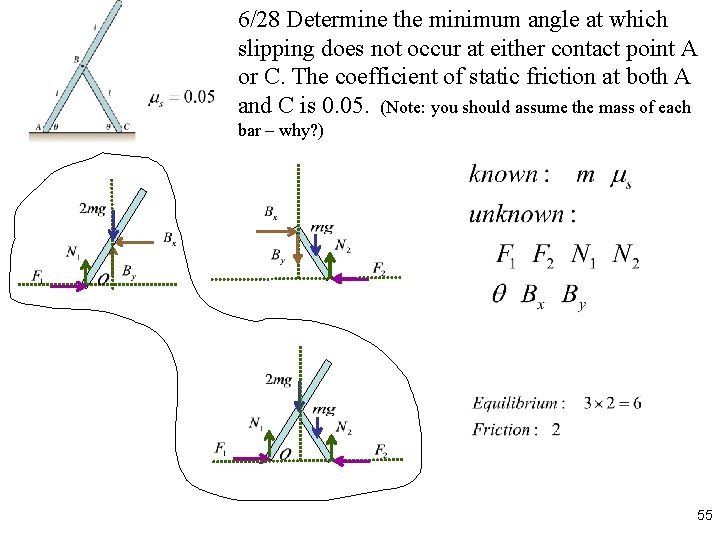
6/28 Determine the minimum angle at which slipping does not occur at either contact point A or C. The coefficient of static friction at both A and C is 0. 05. (Note: you should assume the mass of each bar – why? ) 55

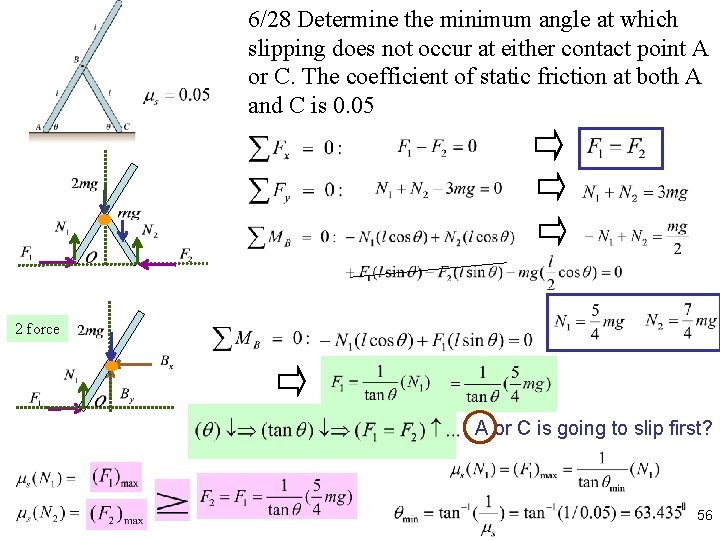
6/28 Determine the minimum angle at which slipping does not occur at either contact point A or C. The coefficient of static friction at both A and C is 0. 05 2 force A or C is going to slip first? 56

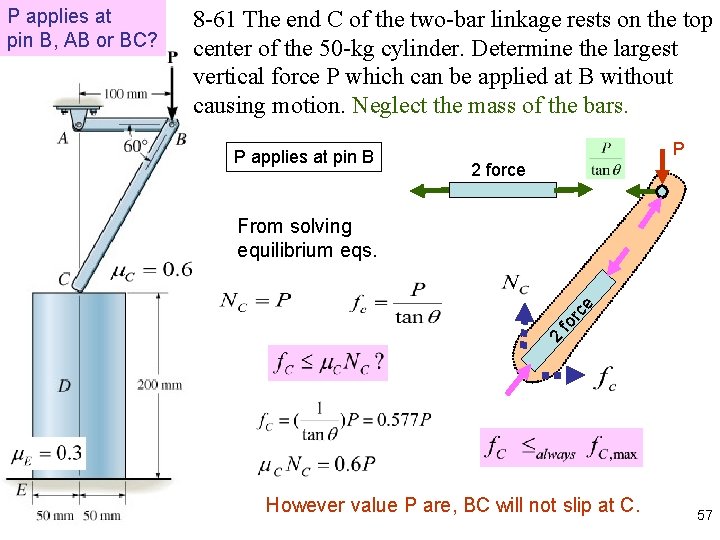
8 -61 The end C of the two-bar linkage rests on the top center of the 50 -kg cylinder. Determine the largest vertical force P which can be applied at B without causing motion. Neglect the mass of the bars. P applies at pin B P 2 force fo rc e From solving equilibrium eqs. 2 P applies at pin B, AB or BC? However value P are, BC will not slip at C. 57

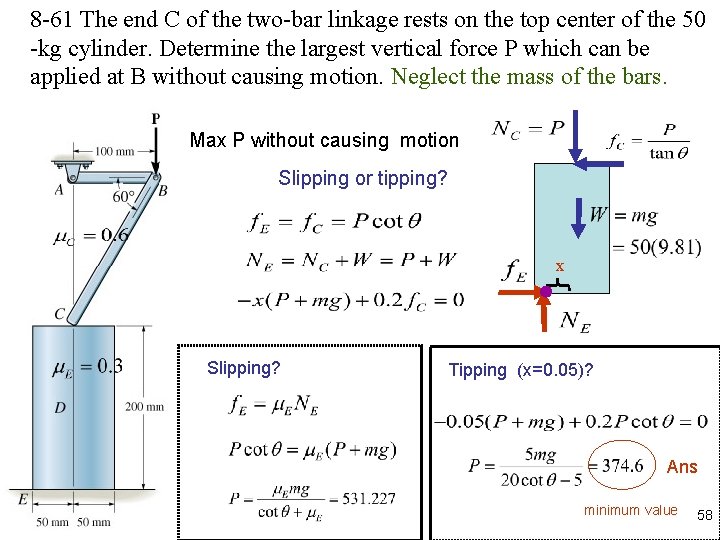
8 -61 The end C of the two-bar linkage rests on the top center of the 50 -kg cylinder. Determine the largest vertical force P which can be applied at B without causing motion. Neglect the mass of the bars. Max P without causing motion Slipping or tipping? x Slipping? Tipping (x=0. 05)? Ans minimum value 58

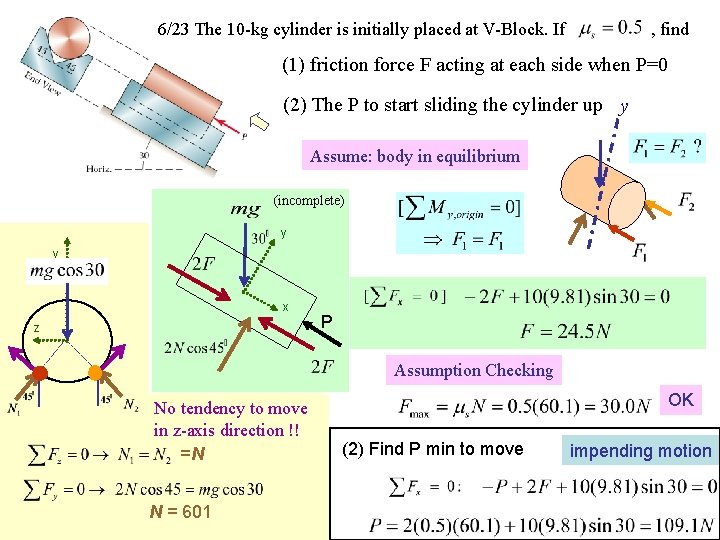
6/23 The 10 -kg cylinder is initially placed at V-Block. If , find (1) friction force F acting at each side when P=0 (2) The P to start sliding the cylinder up y Assume: body in equilibrium (incomplete) y y x z P Assumption Checking No tendency to move in z-axis direction !! =N N = 601 OK (2) Find P min to move impending motion 60

A C B D Determine the minimum coefficient of static friction at each point of contact so that the pile does not collapse. weight W, radius r Think of Equilibrium to find out the relation of F and N 61

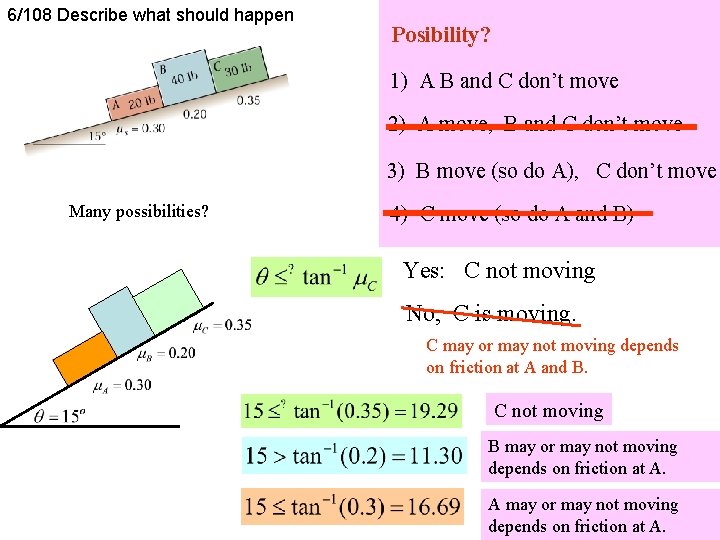
6/108 Describe what should happen Posibility? 1) A B and C don’t move 2) A move, B and C don’t move 3) B move (so do A), C don’t move Many possibilities? 4) C move (so do A and B) Yes: C not moving No, C is moving. C may or may not moving depends on friction at A and B. C not moving B may or may not moving depends on friction at A. A may or may not moving depends on friction at A. 62

6/108 Describe what should happen Assume 1) A and B don’t move, C don’t move = 75. 806 = 379. 03 y = 58. 403 x = 125. 507 Assumption Checking 125. 507 Assumption is wrong ! So, A and B move and C don’t move 63

Recommend Problem 6/16 6/125 6/23 6/41 6/40 6/37 6/108 64