6 6 Systems of Linear Inequalities Word Problems

6. 6 Systems of Linear Inequalities Word Problems Use a system of linear inequalities to model a real-life situation.

Standard Form of Word Problems • • Define variables Write out the system Graph the inequalities Write 2 possible solutions

Word Problem #1 You can work a total of no more than 41 hours each week at your two jobs. Housecleaning pays $5 per hour and your sales job pays $8 per hour. You need to earn at least $254 each week to pay your bills. Write a system of inequalities that shows the various numbers of hours you can work at each job. x = housecleaning hours y = sales job hours Hours: x + y ≤ 41 Money: 5 x + 8 y ≥ 254

Word Problem #2 Fuel x costs $2 per gallon and fuel y costs $3 per gallon. You have at most $18 to spend on fuel. Write and graph a system of linear inequalities to represent this situation. x = gallons of fuel x y = gallons of fuel y Price: Gallons of x: Gallons of y: 2 x + 3 y ≤ 18 x ≥ 0 y ≥ 0

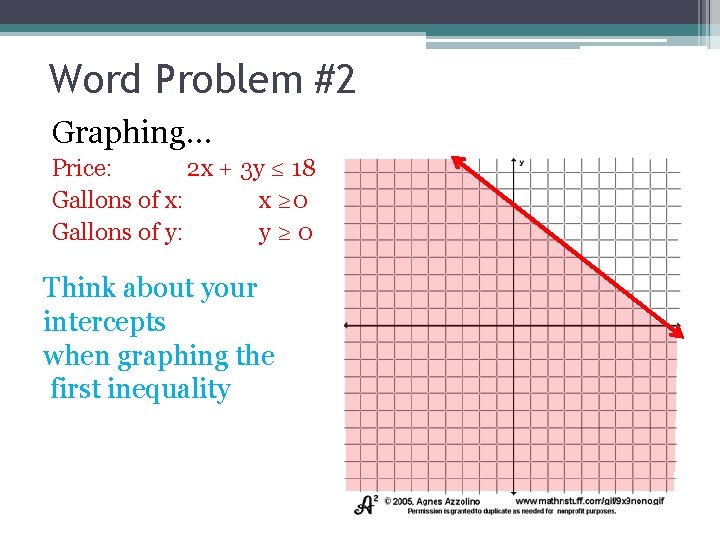
Word Problem #2 Graphing… Price: 2 x + 3 y ≤ 18 Gallons of x: x ≥ 0 Gallons of y: y ≥ 0 Think about your intercepts when graphing the first inequality

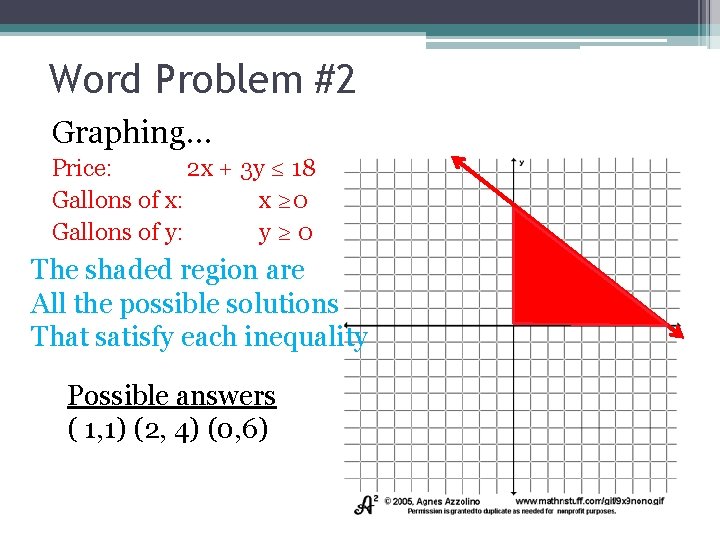
Word Problem #2 Graphing… Price: 2 x + 3 y ≤ 18 Gallons of x: x ≥ 0 Gallons of y: y ≥ 0 The shaded region are All the possible solutions That satisfy each inequality Possible answers ( 1, 1) (2, 4) (0, 6)

Word Problem #3 A salad contains ham and chicken. There at most 6 pounds of ham and chicken in the salad. Write and graph a system of inequalities to represent this situation. x = lbs of ham y = lbs of chicken Total Pounds: Pounds of ham: Pounds of chicken: x + y ≤ 6 x ≥ 0 y ≥ 0

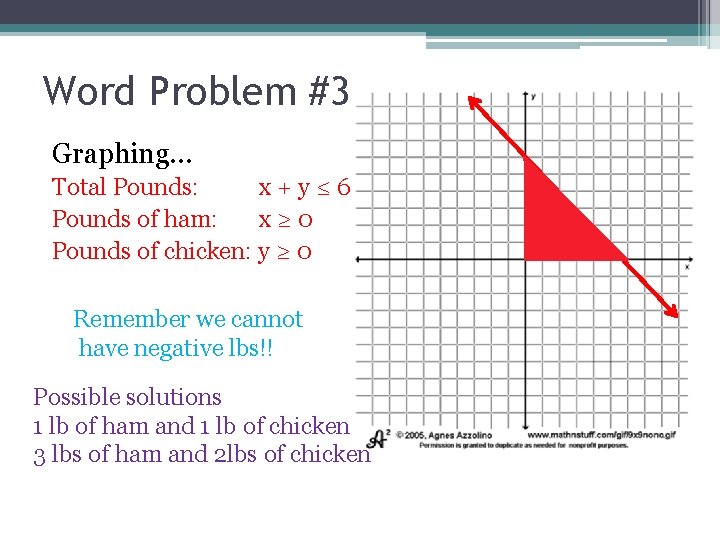
Word Problem #3 Graphing… Total Pounds: x + y ≤ 6 Pounds of ham: x ≥ 0 Pounds of chicken: y ≥ 0 Remember we cannot have negative lbs!! Possible solutions 1 lb of ham and 1 lb of chicken 3 lbs of ham and 2 lbs of chicken

Word Problem #4 •

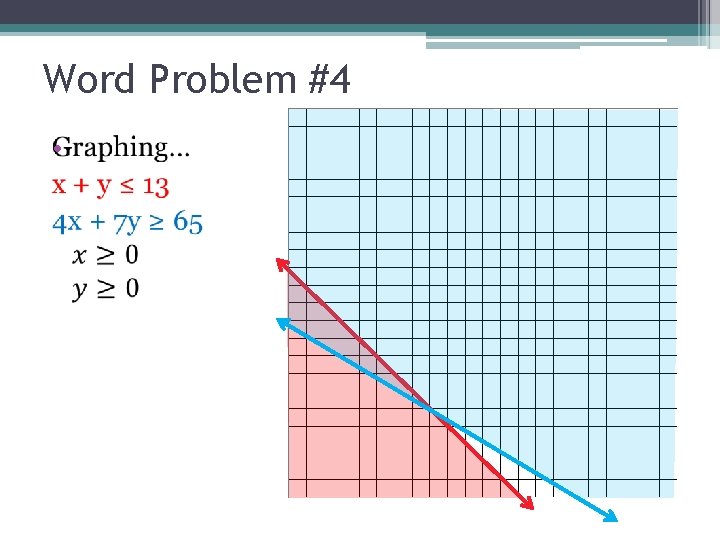
Word Problem #4 •

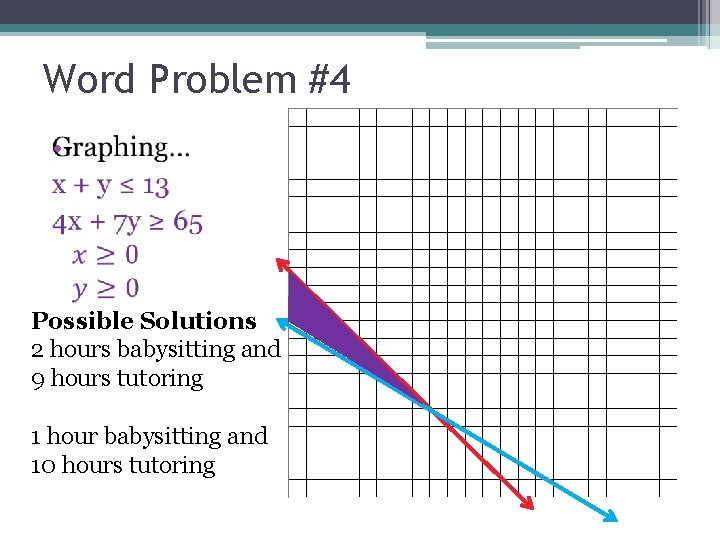
Word Problem #4 • Possible Solutions 2 hours babysitting and 9 hours tutoring 1 hour babysitting and 10 hours tutoring

Example 5 In one week, Ed can mow at most 9 times and rake at most 7 times. He charges $20 for mowing and $10 for raking. He needs to make more than $125 in one week. Show and describe all the possible combinations of mowing and raking that Ed can do to meet his goal. List two possible combinations. Earnings per Job ($) Mowing 20 Raking 10

Example 5 - Continued Step 1 Write a system of inequalities. Let x represent the number of mowing jobs and y represent the number of raking jobs. x≤ 9 y≤ 7 20 x + 10 y > 125 He can do at most 9 mowing jobs. He can do at most 7 raking jobs. He wants to earn more than $125.

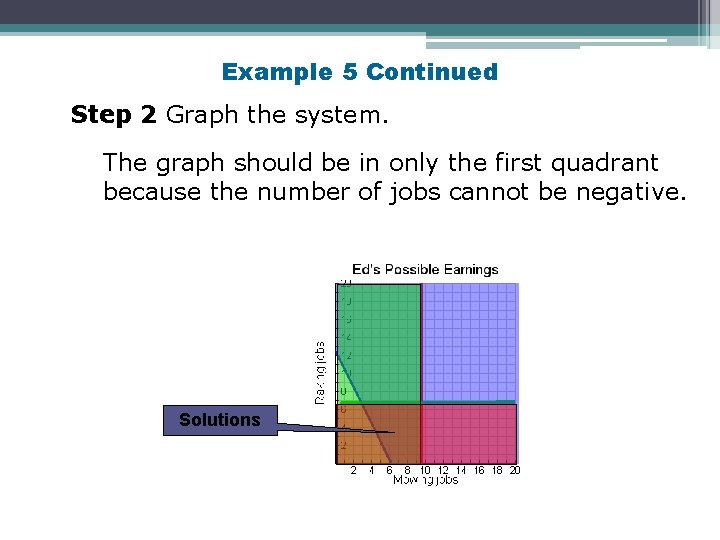
Example 5 Continued Step 2 Graph the system. The graph should be in only the first quadrant because the number of jobs cannot be negative. Solutions

Example 5 - Continued Step 3 Describe all possible combinations. All possible combinations represented by ordered pairs of whole numbers in the solution region will meet Ed’s requirement of mowing, raking, and earning more than $125 in one week. Answers must be whole numbers because he cannot work a portion of a job. Step 4 List the two possible combinations. Two possible combinations are: 7 mowing and 4 raking jobs 8 mowing and 1 raking jobs