6 6 Solve Absolute Value Inequalities EXAMPLE 1

6. 6 Solve Absolute Value Inequalities

EXAMPLE 1 Solve absolute value inequalities Solve the inequality. Graph your solution. a. x –> 6 SOLUTION a. The distance between x and 0 is greater than or equal to 6. So, x ≤ – 6 or x ≥ 6. ANSWER The solutions are all real numbers less than or equal to – 6 or greater than or equal to 6.

EXAMPLE 1 b. Solve absolute value inequalities x < – 0. 5 SOLUTION The distance between x and 0 is less than or equal to 0. 5. So, to – 0. 5 ≤ x ≤ 0. 5. ANSWER The solutions are all real numbers greater than or equal to – 0. 5 and less than or equal to 0. 5.

EXAMPLE 4 forusing Example 1 Find a base the percent equation GUIDED PRACTICE Solve the inequality. Graph your solution. 1. x < 8 SOLUTION a. The distance between x and 0 is less equal to 8. So, – 8 ≤ x ≤ 8. . . – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 6 7 8 9 ANSWER The solutions are all real numbers greater than or equal to – 8 & less than or equal to 8.

EXAMPLE 4 forusing Example 1 Find a base the percent equation GUIDED PRACTICE 2. u < 3. 5 SOLUTION a. The distance between x and 0 is less or equal to 3. 5. So, – 3. 5 ≤ u ≤ 3. 5. . – 4. 5 – 3. 5 – 2. 5 – 1. 5 0 . 1. 5 2. 5 3. 5 4. 5 ANSWER The solutions are all real numbers greater than or equal to – 3. 5 & less than or equal to 3. 5.

EXAMPLE 4 forusing Example 1 Find a base the percent equation GUIDED PRACTICE 3. v > 2 3 SOLUTION a. The distance between x and 0 is less or greater 2 than 2 so, v < – 2 or v > 3 3 3 – 3 2 1 – – 3 3 3 0 1 3 2 3 3 3 ANSWER 2 – The solutions are all real numbers greater than 3 and less than 2 3

EXAMPLE 2 Solve an absolute value inequality Solve x – 5 ≥ 7. Graph your solution. x– 5 > – 7 x – 5< – 7 x< – – 2 Write original inequality. or x – 5 > – 7 Rewrite as compound inequality. or Add 5 to each side. x> – 12 ANSWER The solutions are all real numbers less than or equal to – 2 or greater than or equal to 12. Check several solutions in the original inequality.
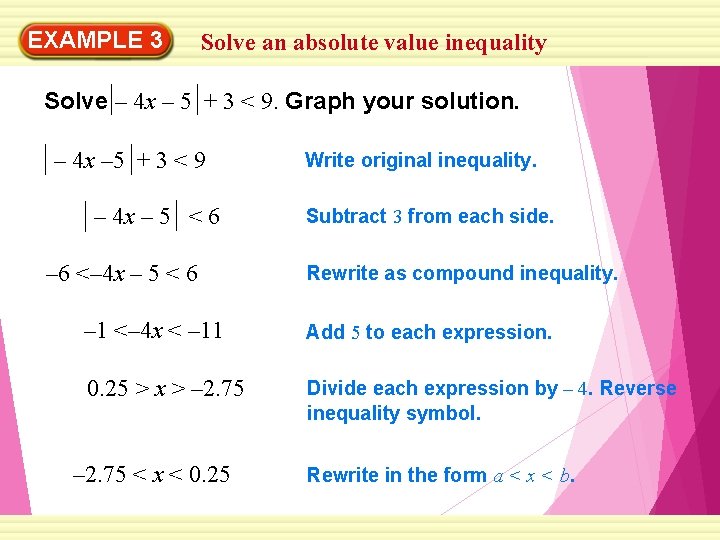
EXAMPLE 3 Solve an absolute value inequality Solve – 4 x – 5 + 3 < 9. Graph your solution. – 4 x – 5 + 3 < 9 – 4 x – 5 < 6 – 6 <– 4 x – 5 < 6 Write original inequality. Subtract 3 from each side. Rewrite as compound inequality. – 1 <– 4 x < – 11 Add 5 to each expression. 0. 25 > x > – 2. 75 Divide each expression by – 4. Reverse inequality symbol. – 2. 75 < x < 0. 25 Rewrite in the form a < x < b.
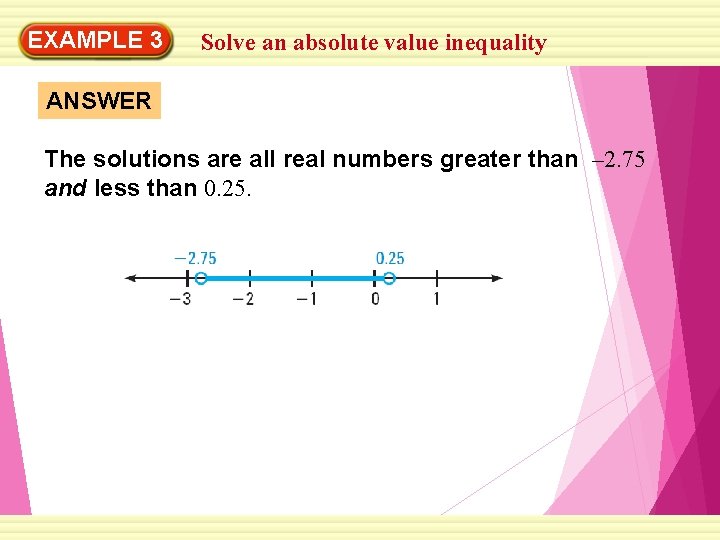
EXAMPLE 3 Solve an absolute value inequality ANSWER The solutions are all real numbers greater than – 2. 75 and less than 0. 25.

GUIDED PRACTICE for Examples 2 and 3 Solve the inequality. 4. x+3 >8 SOLUTION x+3 >8 Write original inequality. x + 3 < 8 or x + 3 > 8 x < – 11 or x > 5 Rewrite as compound inequality. Add – 3 to each side. ANSWER The solutions are all real numbers less than – 11 or greater than to 5.

GUIDED PRACTICE 5. for Examples 2 and 3 2 w – 1 < 11 SOLUTION 2 w – 1 < 11 2 w – 1 < – 11 or 2 w – 1 > 11 Write original inequality. Rewrite as compound inequality. 2 w < – 10 or 2 w > 12 Add 1 to each side. w<– 5 or w > 6 Divide by 2 to each side ANSWER – 5 < w <– 6

GUIDED PRACTICE 6. for Examples 2 and 3 3 5 m – 6 – 8 < – 13 SOLUTION 3 5 m – 6 – 8 < – 13 Write original inequality. 3 5 m – 6 < – 21 Add 8 to each side. |5 m – 6| <– 7 – 7< – 5 m 6 < – 7 Divide by each side by 3. Rewrite as compound inequality.

GUIDED PRACTICE for Examples 2 and 3 – 1< – 13 – 5 m < Add 6 to each side. – 0. 2 < – 2. 6 – m < Simplify. ANSWER The solutions are all real numbers greater than or equal to – 0. 2 and less than or equal to 2. 6.

EXAMPLE 4 Solve a multi-step problem Computers You are buying a new computer and find 10 models in a store advertisement. The prices are $890, $750, $650, $370, $660, $670, $450, $650, $725, and $825. Find the mean of the computer prices. You are willing to pay the mean price with an absolute deviation of at most $100. How many of the computer prices meet your condition?

EXAMPLE 4 Solve a multi-step problem SOLUTION STEP 1 Find the mean by dividing the sum of the prices by 10. Mean = 890 + 750 + 650 + 370 + 660 + 670 + 450 + 650 + 725 + 825 10 6640 = 10 = 664

EXAMPLE 4 Solve a multi-step problem STEP 2 Write and solve an inequality. An absolute deviation of at most $100 from the mean, $664, is given by the inequality x – 664 ≤ 100 – 100 ≤ x – 664 ≤ 100 564 ≤ x ≤ 764 Write absolute value inequality. Write as compound inequality. Add 664 to each expression.

EXAMPLE 4 Solve a multi-step problem ANSWER The prices you will consider must be at least $564 and at most $764. Six prices meet your condition: $750, $660, $670, $650, and $725.

GUIDED PRACTICE 7. for Example 4 WHAT IF? In Example 4, suppose that you are willing to pay the mean price with an absolute deviation of at most $75. How many of the computer prices meet this condition? SOLUTION STEP 1 Find the mean by dividing the sum of the prices by 10. 890 + 750 + 650 + 370 + 660 + 670 + 450 + 650 + 725 + 825 Mean = 10 6640 = 10 = 664

GUIDED PRACTICE for Example 4 STEP 2 Write and solve an inequality. An absolute deviation of at most $75 from the mean, $664, is given by the inequality x – 664 ≤ 75 – 75 ≤ x – 664 ≤ 75 589 ≤ x ≤ 739 Write absolute value inequality. Write as compound inequality. Add 664 to each expression.

GUIDED PRACTICE for Example 4 ANSWER The prices you will consider must be at least $589 and at most $739. 5 prices meet your condition: $650, $660, $670, $650, and $725.
- Slides: 20