6 6 Fundamental Theoremof of Algebra Objectives Use

6 -6 Fundamental. Theoremof of. Algebra Objectives Use the Fundamental Theorem of Algebra and its corollary to write a polynomial equation of least degree with given roots. Identify all of the roots of a polynomial equation. Holt Algebra 22

6 -6 Fundamental Theorem of Algebra You have learned several important properties about real roots of polynomial equations. You can use this information to write polynomial function when given in zeros. Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Example 1: Writing Polynomial Functions Write the simplest polynomial with roots – 1, 2 , 3 and 4. If r is a zero of P(x), then x – r is a factor of P(x). Multiply the first two binomials. Multiply the trinomial by the binomial. 2 8 P(x) = x 3 – 11 x – 2 x + 3 3 Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Check It Out! Example 1 a Write the simplest polynomial function with the given zeros. – 2, 2, 4 If r is a zero of P(x), then x – r is a factor of P(x). Multiply the first two binomials. Multiply the trinomial by the binomial. P(x) = x 3– 4 x 2– 4 x + 16 Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Check It Out! Example 1 b Write the simplest polynomial function with the given zeros. 0, 2 3 , 3 If r is a zero of P(x), then x – r is a factor of P(x). Multiply the first two binomials. Multiply the trinomial by the binomial. 2 P(x) = x 3– 11 x + 2 x 3 Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Notice that the degree of the function in Example 1 is the same as the number of zeros. This is true for all polynomial functions. However, all of the zeros are not necessarily real zeros. Polynomials functions, like quadratic functions, may have complex zeros that are not real numbers. Holt Algebra 2

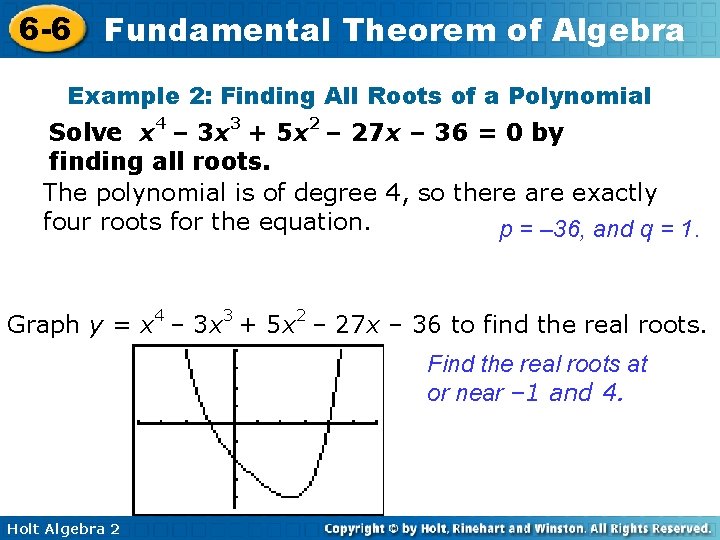
6 -6 Fundamental Theorem of Algebra Example 2: Finding All Roots of a Polynomial Solve x 4 – 3 x 3 + 5 x 2 – 27 x – 36 = 0 by finding all roots. The polynomial is of degree 4, so there are exactly four roots for the equation. p = – 36, and q = 1. Graph y = x 4 – 3 x 3 + 5 x 2 – 27 x – 36 to find the real roots. Find the real roots at or near – 1 and 4. Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Example 2 Continued Test the possible real roots. Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Example 2 Continued The polynomial factors into (x + 1)(x – 4)(x 2 + 9) = 0. The solutions are 4, – 1, 3 i, – 3 i. Holt Algebra 2

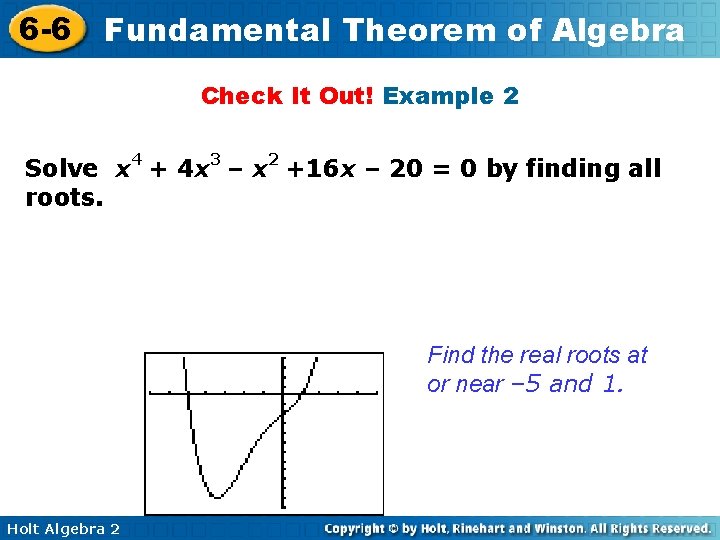
6 -6 Fundamental Theorem of Algebra Check It Out! Example 2 Solve x 4 + 4 x 3 – x 2 +16 x – 20 = 0 by finding all roots. Find the real roots at or near – 5 and 1. Holt Algebra 2

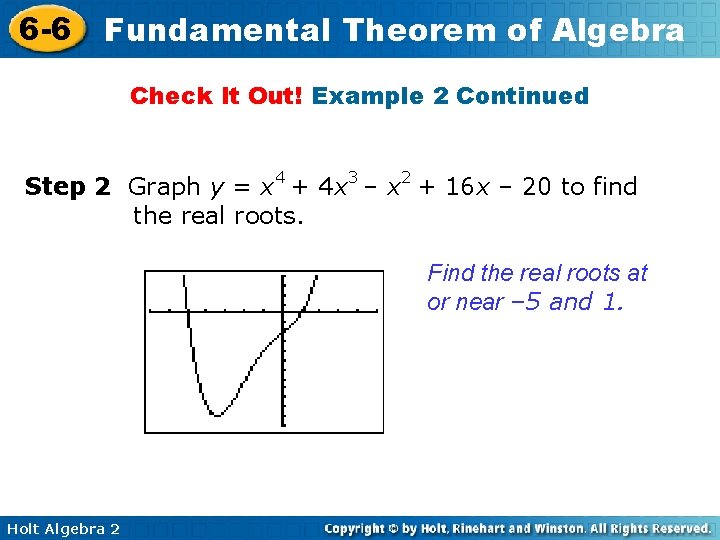
6 -6 Fundamental Theorem of Algebra Check It Out! Example 2 Continued Step 2 Graph y = x 4 + 4 x 3 – x 2 + 16 x – 20 to find the real roots. Find the real roots at or near – 5 and 1. Holt Algebra 2

6 -6 Fundamental Theorem of Algebra Check It Out! Example 2 Continued The polynomial factors into (x + 5)(x – 1)(x 2 + 4) = 0. The solutions are – 5, 1, – 2 i, +2 i). Holt Algebra 2

6 -6 Fundamental Theorem of Algebra HOMEWORKPage 449 # 1 -6, 11 -19 Holt Algebra 2