6 5 Properties and Applications of Matrices Learn

Matrix Notation A general element of a matrix is denoted aij. The ij refers

Example: Determining matrix elements Let aij denote a general element in A, and bij

Example: Determining matrix elements Solution (a) Element a 12 is located in the 1

Example: Determining matrix elements Compute a 31 b 13 + a 32 b 23

Operations on Matrices Matrix Addition The sum of two m n matrices A and

Operations on Matrices Matrix Subtraction The difference of two m n matrices A and

Operations on Matrices Multiplication of a Matrix by a Scalar The product of a

Example: Performing operations on matrices If possible, perform the indicated operations using (a) A

Example: Performing operations on matrices Solution (a) A + 3 B Copyright © 2014,

Example: Performing operations on matrices (b) A – C is undefined because the dimension

Example: Performing operations on matrices (c) – 2 C 3 D Copyright © 2014,

Matrix Multiplication The product of an m n matrix A and an n k

Matrix Multiplication Copyright © 2014, 2010, 2006 Pearson Education, Inc. 14

Example: Multiplying matrices If possible, compute each product using a) AB b) CA (c)

Example: Multiplying matrices Solution (a) AB = Copyright © 2014, 2010, 2006 Pearson Education,

Example: Multiplying matrices Solution (b) CA = Copyright © 2014, 2010, 2006 Pearson Education,

Example: Multiplying matrices Solution c) The dimension of D is 3 3 and the

Properties of Matrices Let A, B, and C be matrices. Assume that each matrix

Slides: 19

Download presentation

6. 5 Properties and Applications of Matrices Learn matrix notation Learn how matrices are used in social networks Find sums, differences, and scalar multiples of matrices ♦ Find matrix products ♦ Use technology (optional) ♦ ♦ ♦ Copyright © 2014, 2010, 2006 Pearson Education, Inc. 1

Matrix Notation A general element of a matrix is denoted aij. The ij refers to an element in the ith row, jth column. For example, a 31 would be an element in matrix A located in the third row, first column. The matrices are equal if corresponding elements are equal. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 2

Example: Determining matrix elements Let aij denote a general element in A, and bij denote a general element in B, where (a) Identify a 12, b 32 and a 13. (b) Compute a 31 b 13 + a 32 b 23 + a 33 b 33. (c) Is there a value for x that will make the statement A = B true? Copyright © 2014, 2010, 2006 Pearson Education, Inc. 3

Example: Determining matrix elements Solution (a) Element a 12 is located in the 1 st row and 2 nd column of A = 3. b 32 = 2 (row 3, column 2) a 13= 4 (row 1, column 3) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 4

Example: Determining matrix elements Compute a 31 b 13 + a 32 b 23 + a 33 b 33. = (4)(7) + (2)(– 2) + (5)(2) = 34 (c) No, since a 32 = 2 ≠ 5 = b 32 and a 33 = 5 ≠ 2 = b 32. So A ≠ B. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 5

Operations on Matrices Matrix Addition The sum of two m n matrices A and B is the m n matrix A + B, in which each element is the sum of the corresponding elements of A and B. This is written as A + B = [aij] + [bij] = [aij + bij]. If A and B have different dimensions, then A + B is undefined. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 6

Operations on Matrices Matrix Subtraction The difference of two m n matrices A and B is the m n matrix A – B, in which each element is the difference of the corresponding elements of A and B. This is written as A – B = [aij] – [bij] = [aij – bij]. If A and B have different dimensions, then A – B is undefined. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 7

Operations on Matrices Multiplication of a Matrix by a Scalar The product of a scalar (real number) k and an m n matrix A is the m n matrix k. A, in which each element is k times the corresponding element of A. This is written as k. A = k[aij] = [kaij]. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 8

Example: Performing operations on matrices (b) A – C is undefined because the dimension of A is 2 2 and unequal to the dimension of C, which is 3 2. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 11

Matrix Multiplication The product of an m n matrix A and an n k matrix B is the m k matrix AB, which is computed as follows. To find the element of AB in the ith row and jth column, multiply each element in the ith row of A by the corresponding element in the jth column of B. The sum of these products will give the element in row i, column j of AB. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 13

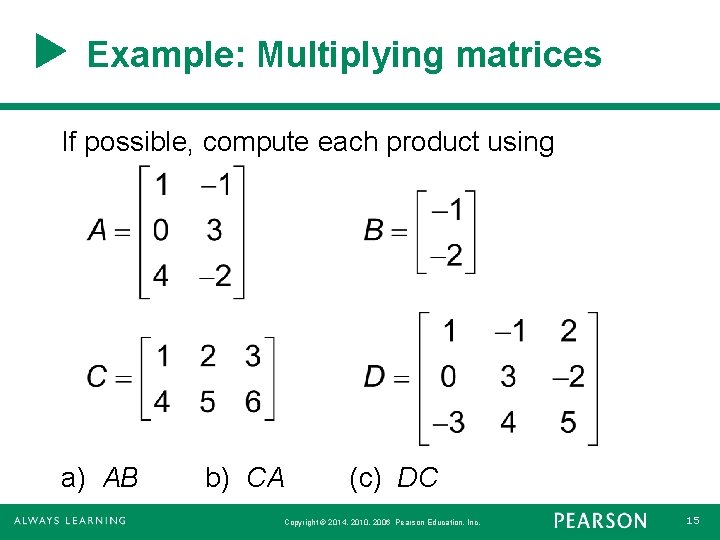
Example: Multiplying matrices Solution c) The dimension of D is 3 3 and the dimension of C is 2 3. Therefore DC is undefined. The number of columns in D (3) does not match the number of rows in C (2). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 18

Properties of Matrices Let A, B, and C be matrices. Assume that each matrix operation is defined. 1. 2. 3. 4. A+B=B+A (A + B) + C = A + (B + C) (AB)C = A(BC) A(B + C) = AB + AC Copyright © 2014, 2010, 2006 Pearson Education, Inc. 19