6 5 PARABOL AS Objective To find equations

6 -5 PARABOL AS Objective: To find equations of parabolas and to graph them.

HAPPY NEW YEAR EVERYONE

MORE PREREQUISITE SKILLS Plot each pair of points, and then find the distance between them. 1 (5, 20); (2, 6) 2 (0, 0) ; (x, y) (for number two leave the distance in terms of x and y, and place an arbitray point on your graph)

CONIC SECTIONS PARABOLAS The parabola has the characteristic shape shown above. A parabola is defined to be the “set of points the same distance from a

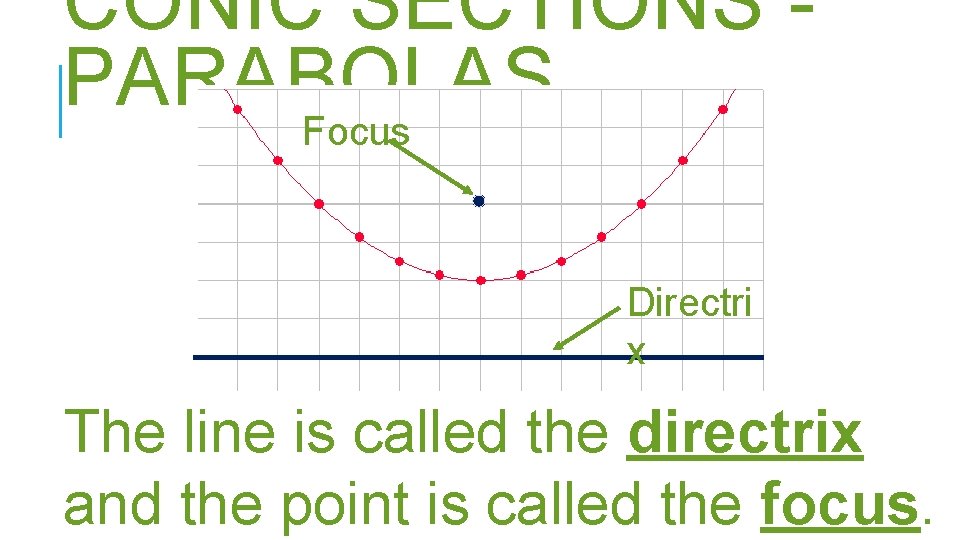
CONIC SECTIONS PARABOLAS Focus Directri x The line is called the directrix and the point is called the focus.

CONIC SECTIONS PARABOLAS Foc us Axis of Symmetr y Directrix Verte x The line perpendicular to the directrix passing through the focus is the axis of symmetry. The vertex is the point of intersection of the axis of symmetry with the parabola.

CONIC SECTIONS PARABOLAS Focus d 1 d 2 Directrix The definition of the parabola is the set of points the same distance from the focus and directrix. Therefore, d 1 = d 2 for any point (x, y) on the parabola.

FINDING THE FOCUS AND 6. 5 Parabola s

CONIC SECTIONS PARABOLAS Focus y = ax 2 p p Directrix We know that a parabola has a basic equation y = ax 2. The vertex is at (0, 0). The distance from the vertex to the focus and directrix is the same. Let’s call it p.

CONIC SECTIONS PARABOLAS Focus ( ? , ? ) y = ax 2 p Directrix ? ? ? p ( 0, 0) Find the point for the focus and the equation of the directrix if the vertex is at (0, 0). (In terms of

CONIC SECTIONS PARABOLAS Focus ( 0, p) y = ax 2 p Directrix ? ? ? p ( 0, 0) The focus is p units up from (0, 0), so the focus is at the point (0, p).

CONIC SECTIONS PARABOLAS Focus ( 0, p) y = ax 2 p Directrix ? ? ? p ( 0, 0) The directrix is a horizontal line p units below the origin. Find the equation of the directrix.

CONIC SECTIONS PARABOLAS Focus ( 0, p) y = ax 2 p Directrix y = -p p ( 0, 0) The directrix is a horizontal line p units below the origin or a horizontal line through the point (0, -p). The equation is y = -p.

CONIC SECTIONS PARABOLAS Focus ( 0, p) ( x, y) d 1 y = ax 2 Directrix y = -p ( 0, 0) d 2 The definition of the parabola indicates the distance d 1 from any point (x, y) on the curve to the focus and the distance d 2 from the point to the directrix must be equal.

CONIC SECTIONS PARABOLAS Focus ( 0, p) ( x, ax 2) d 1 y = ax 2 Directrix y = -p ( 0, 0) d 2 However, the parabola is y = ax 2. We can substitute for y in the point (x, y). The point on the

CONIC SECTIONS PARABOLAS Focus ( 0, p) ( x, ax 2) d 1 y = ax 2 Directrix y = -p ( 0, 0) d 2 ( ? , ? ) What is the coordinates of the point on the directrix immediately below the point (x, ax 2)?

CONIC SECTIONS PARABOLAS Focus ( 0, p) ( x, ax 2) d 1 y = ax 2 Directrix y = -p ( 0, 0) d 2 ( x, -p) The x value is the same as the point (x, ax 2) and the y value is on the line y = -p, so the point must

CONIC SECTIONS PARABOLAS Focus ( 0, p) ( x, ax 2) d 1 y = ax 2 Directrix y = -p ( 0, 0) d 2 ( x, -p) d 1 is the distance from (0, p) to (x, ax 2). d 2 is the distance from (x, ax 2) to (x, -p) and d 1 = d 2. Use the distance formula to solve for p.

CONIC SECTIONS d 1 PARABOLAS is the distance from (0, p) to (x, ax ). d 2 is the 2 distance from (x, ax 2) to (x, -p) and d 1 = d 2. Use the distance formula to solve d for = dp. 1 2

CONIC SECTIONS PARABOLAS Therefore, the distance p from the vertex to the focus and the vertex to the directrix is given by the formula depending on the direction of the parabola.

PARABOLA EQUATION 6. 5 Parabolas

PARABOLA EQUATION CENTER AT THE ORIGIN (0, 0) p p p (p, 0) p p)

CONIC SECTIONS PARABOLAS Using transformations, we can shift the parabola y=ax 2 horizontally and vertically. The vertex is shifted from (0, 0) to (h, k). Recall that when “a” is positive, the graph opens up. When “a” is negative, the graph reflects about the x-axis and opens down.

PARABOLA EQUATION CENTER AT (H, K)

EXAMPLES GRAPH A PARABOLA. FIND THE VERTEX, FOCUS AND DIRECTRIX. 6. 5 Parabolas

EXAMPLE 1 FIND THE FOCUS AND DIRECTRIX OF EACH PARABOLA

EXAMPLE 2 FIND AN EQUATION OF THE PARABOLA WITH VERTEX (0, 0) AND DIRECTRIX X = 2. Sketch the information.

PARABOLA. FIND THE VERTEX, FOCUS, AND DIRECTRIX. The vertex is (-2, -3). The parabola opens

Find the focus and directrix. The focus and directrix are “p” units from the vertex where The focus and directrix are 2 units from the

Find the focus and directrix. 2 Units Focus: (-2, -1) Directrix: y = -5

EXAMPLE 4 WRITE THE EQUATION OF A PARABOLA WITH VERTEX AT (3, 2) AND FOCUS AT (-1, 2). Plot the known points. What can be determined from these points?

EXAMPLE 4 WRITE THE EQUATION OF A PARABOLA WITH VERTEX AT (3, 2) AND FOCUS AT (-1, The 2). distance from the vertex to the focus is 4, so p = 4.

HOMEWO RK Page 240 #1 -17 odds