6 5 Complex Numbers in Polar Form De

6. 5 Complex Numbers in Polar Form: De. Moivre’s Theorem • Objectives – Fine absolute value of a complex # – Write complex # in polar form – Convert a complex # from polar to rectangular form – Plot complex numbers in the complex plane – Find products & quotients of complex numbers in polar form – Find powers of complex # in polar form – Find roots of complex # in polar form

Complex number = z = a + bi • • a is a real number bi is an imaginary number Together, the sum, a+bi is a COMPLEX # Complex plane has a real axis (horizontal) and an imaginary axis (vertical) • 2 – 5 i is found in the 4 th quadrant of the complex plane (horiz = 2, vert = -5) • Absolute value of 2 – 5 i refers to the distance this pt. is from the origin (continued)

Find the absolute value • Since the horizontal component = 2 and vertical = -5, we can consider the distance to that point as the same as the length of the hypotenuse of a right triangle with those respective legs
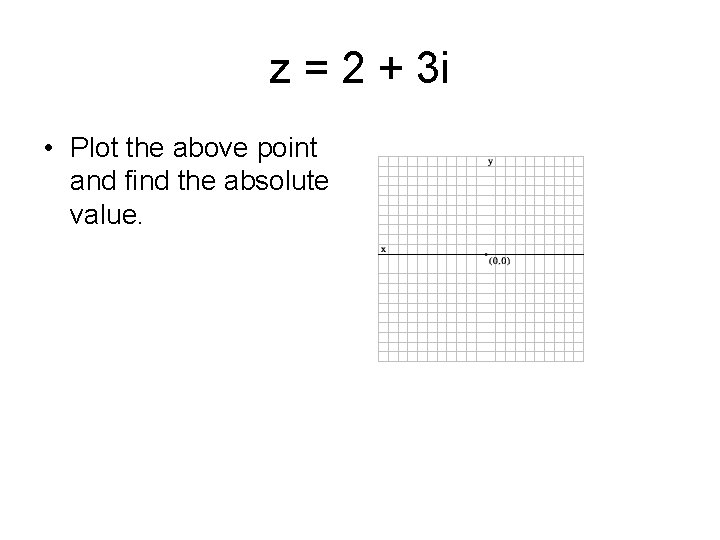
z = 2 + 3 i • Plot the above point and find the absolute value.

z = -2 + -3 i • Plot the above point and find the absolute value.

Expressing complex numbers in polar form • z = a + bi

Express z = -5 + 3 i in complex form
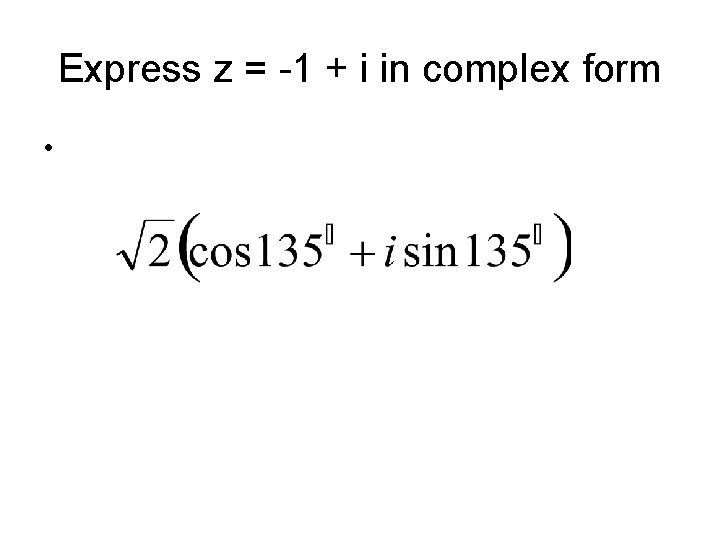
Express z = -1 + i in complex form •

Express z = -6 + 3 i in complex form •

Product & Quotient of complex numbers
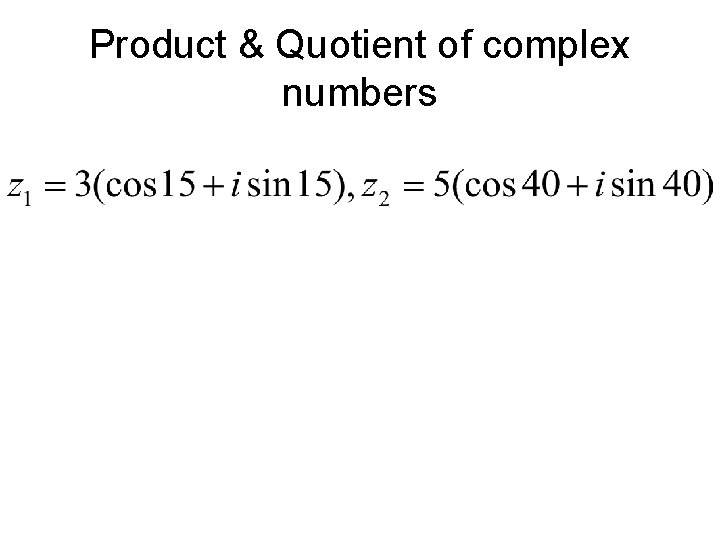
Product & Quotient of complex numbers

Product & Quotient of complex numbers

Product & Quotient of complex numbers

Product & Quotient of complex numbers

Multiplying complex numbers together leads to raising a complex number to a given power • If r is multiplied by itself n times, it creates • If the angle, theta, is added to itself n times, it creates the new angle, (n times theta) • THUS,

Multiplying complex numbers together leads to raising a complex number to a given power • Find

Multiplying complex numbers together leads to raising a complex number to a given power • Find

Multiplying complex numbers together leads to raising a complex number to a given power • Find

Multiplying complex numbers together leads to raising a complex number to a given power • Find

Taking a root (De. Moivre’s Theorem) • Radian Degree Where k = 0, 1, 2, …n-1

If you’re working with degrees add 360/n to the angle measure to complete the circle. • Example: Find the 6 th roots of z= -2 + 2 i • Express in polar form, find the 1 st root, then add 60 degrees successively to find the other 5 roots.

• Example: Find the 4 th roots of z= -1 + 1 i

• Example: Find the 4 th roots of

• Example: Find the cube roots of 8, in degrees.

• Example: Find the cube roots of 27, in radians.
- Slides: 25