6 5 Basic Trigonometric Identities Objective Develop basic

6. 5 Basic Trigonometric Identities Objective: Develop basic trigonometric identities.

Trigonometric Identities � Trigonometric identities are equations that are true for all values of the variable for which the equation is defined. They are most often used to simplify an expression. � Algebraic rules are the same for trigonometric expressions, the notation is sometimes just slightly different.
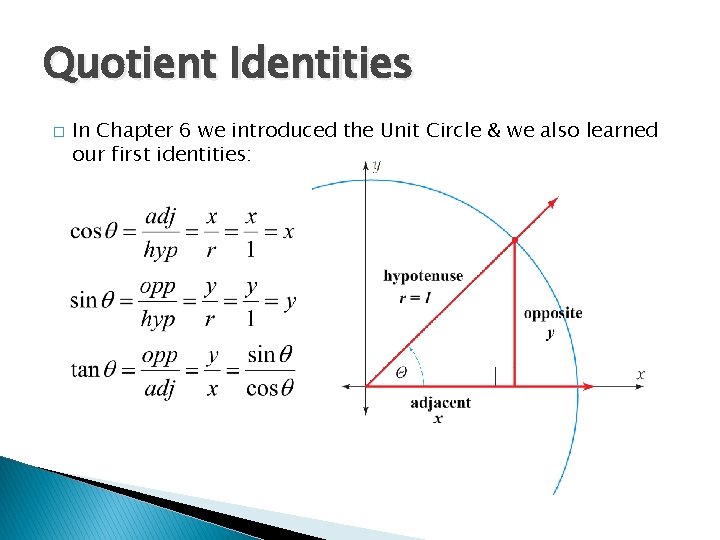
Quotient Identities � In Chapter 6 we introduced the Unit Circle & we also learned our first identities:

Reciprocal Identities � We also learned the reciprocal identities.

Example #1 � Simplify A) the following expressions: B)

Example #2 �

Pythagorean Identities � Using the Pythagorean Theorem & the Unit Circle, the Pythagorean Identities are created:

Pythagorean Identities continued… Be very careful when using Pythagorean identities, the expressions must be squared:

Example #3 � Simplify the following expressions. A) This problem utilizes two identities:

Example #3 � Simplify B) the following expressions. Two identities are also used here:

Example #4 � Use the Quotient, Reciprocal, and Pythagorean identities to find the remaining 5 trigonometric functions.
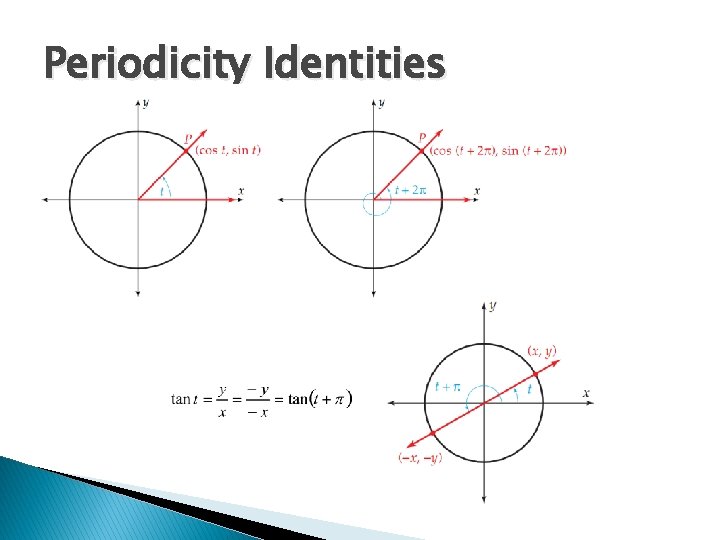
Periodicity Identities

Periodicity Identities

Negative Angle Identities

Example #5 � Simplify the following expression. This problem required first factoring the top and using the identity: After the substitution, the bottom was factored and the top rearranged. Canceling like terms gives the answer shown.

Example #6 � Simplify the following expression. Here the expression has a GCF factored out first. Then a substitution is made with this identity: Then the reciprocal identity is used and like terms are canceled. Finally, the reciprocal identity is used again.
- Slides: 16