6 3 The Universal Wave Equation A wave

Example: The distance between successive crests in a series of water waves is 4.

Homework • Pg 211 #1, 2 (top) • Pg 211 #1 -8 (bottom)

6. 4 Transmission and Reflections of Waves behave in various ways. A change in

Reflection When waves undergo fixed end reflection the pulse is inverted. If the reflection

Fixed end Free end Reflected pulse is inverted Reflected wave is not inverted

Transmission • When a wave travels into a new medium partial reflection occurs. Some

• Fast to Slow Medium (Less dense to more dense Medium) • The

• Slow to Fast Medium (More dense to less dense Medium) • The

6. 6 Interference of Waves • Wave interference occurs when two waves act simultaneously

Destructive Interference • Destructive interference occurs when a crest meets a trough. The crest

Constructive Interference • Constructive interference occurs when crests meet crests (supercrests) or troughs meet

Superposition Principle • The concept of adding the amplitudes of waves is known as

Waves approach each other Overlap Resulting Wave Pattern Remember this pattern only appears for

6. 7 Mechanical Resonance • Resonance is the response of an object that is

• Every object has a natural frequency at which it will vibrate. A

• If you push someone on a swing at the right time they

Tacoma Narrows • Mechanical Resonance in a Bridge

Slides: 20

Download presentation

6. 3 The Universal Wave Equation A wave travels one wavelength in one period of time. f = frequency l= wavelength The speed of a wave is a property of the medium it travels in.

Example: The distance between successive crests in a series of water waves is 4. 0 m. The crests travel 9. 0 m in 4. 5 s. What is the frequency of the crests?

Homework • Pg 211 #1, 2 (top) • Pg 211 #1 -8 (bottom)

6. 4 Transmission and Reflections of Waves behave in various ways. A change in the medium in which a wave is traveling often results in a change of the speed of the wave. The frequency of the wave or disturbance will never change, however, the wavelength of the wave must change if the Universal Wave Equation is to be upheld. Changes to the speed of the wave will ensure proportional changes in the wavelength of the wave.

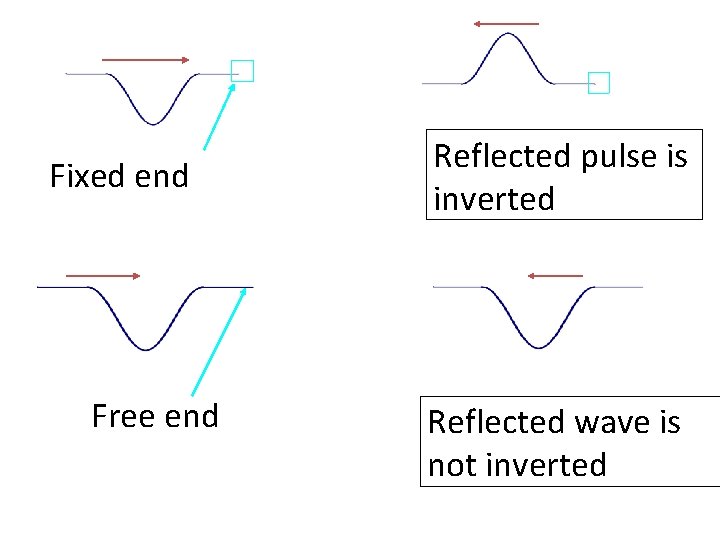
Reflection When waves undergo fixed end reflection the pulse is inverted. If the reflection occurs from a free end then there is no inversion. In both fixed end and free end reflection there is no change in frequency or wavelength. There is also no change in the speed of the pulse since the medium is the same.

Fixed end Free end Reflected pulse is inverted Reflected wave is not inverted

Transmission • When a wave travels into a new medium partial reflection occurs. Some of the energy of the wave is transferred through to the new medium, but some is also reflected back into the original medium. Of course, since the wave is traveling into a new medium there will be a change in its wavelength and speed. The loss of energy also means a decrease in amplitude for the wave.

• Fast to Slow Medium (Less dense to more dense Medium) • The slow medium acts like a rigid obstacle, and the reflected wave is inverted. The transmitted wave is not inverted, travels with reduced speed and wavelength and has a diminished amplitude. Incident Pulse

• Slow to Fast Medium (More dense to less dense Medium) • The fast medium acts like a free end and the reflected wave is not inverted. The transmitted wave is not inverted, travels with increased speed and wavelength and has a diminished amplitude Incident Pulse

Homework • Pg 213 #1, 2 • Pg 214 #1, 2

6. 6 Interference of Waves • Wave interference occurs when two waves act simultaneously on the particles of a medium. There are two types of interference: constructive and destructive.

Destructive Interference • Destructive interference occurs when a crest meets a trough. The crest and trough cancel one another out and a node forms.

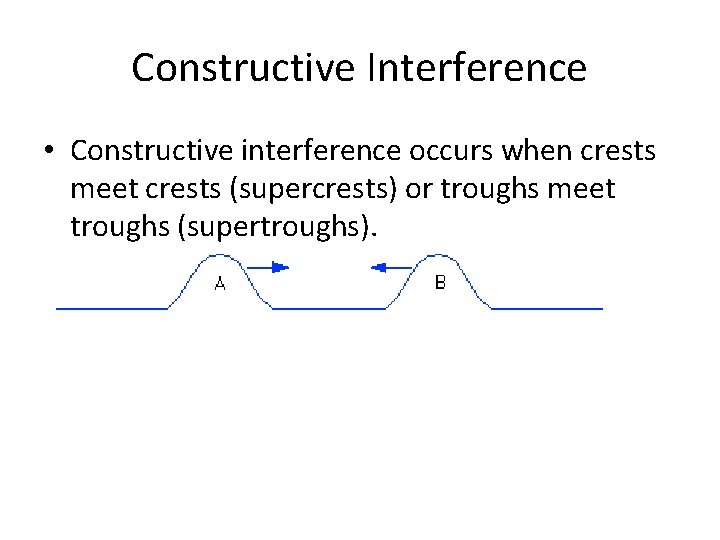
Constructive Interference • Constructive interference occurs when crests meet crests (supercrests) or troughs meet troughs (supertroughs).

Superposition Principle • The concept of adding the amplitudes of waves is known as the superposition principle. It states that at any point the resulting amplitude of two interfering waves is the algebraic sum of the displacements of the individual amplitudes.

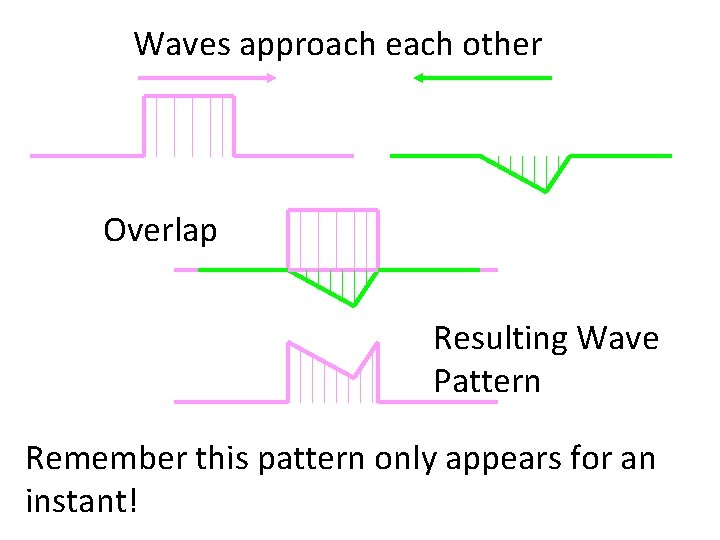
Waves approach each other Overlap Resulting Wave Pattern Remember this pattern only appears for an instant!

6. 7 Mechanical Resonance • Resonance is the response of an object that is free to vibrate to a periodic force with the same frequency as the natural frequency of the object. Therefore resonance is also a transfer of energy from one object to another having the same natural frequency. If the two objects are touching, it is known as mechanical resonance.

• Every object has a natural frequency at which it will vibrate. A swing’s natural frequency will depend on the length of the chains. A window rattles with its natural frequency. Bridges, propellers, blades, turbines, glasses and many types of equipment all have a natural frequency. Read p. 223 -224 for examples.

• If you push someone on a swing at the right time they will travel higher and higher on a swing (with the swing’s natural frequency). Think what would happen if a bridge got “pushed” at the right time over and over. . . Tacoma narrows, swing set, army marches • When an object vibrates in resonance with another, it is called a sympathetic vibration.

Tacoma Narrows • Mechanical Resonance in a Bridge