6 3 Sampling Distributions Sampling Distributions Definition 6

6. 3 Sampling Distributions

Sampling Distributions Definition 6. 9 -P 107 The probability distribution of a statistic is called a sampling distribution.

6. 3. 1 Chi-squared Distribution Theorem Let , the distribution of the random variable , where by the density function is given This is known as the chi-squared distribution with degrees of freedom. Denoted by

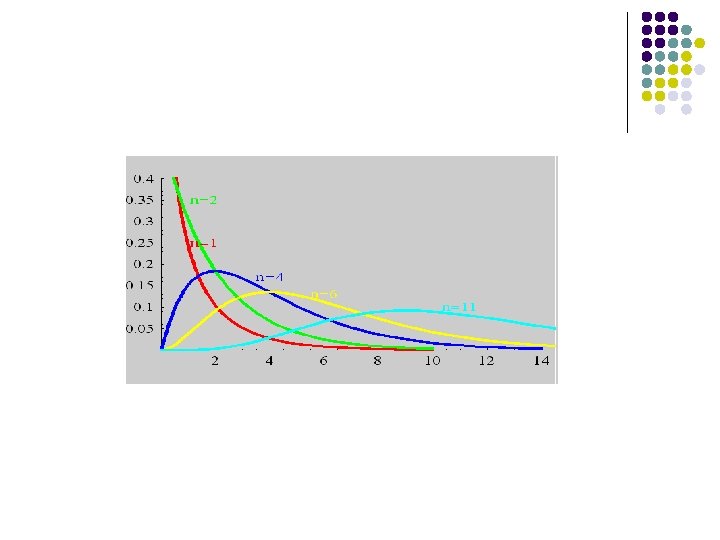
Properties : 1. If are independent ，and Xi~ then 2. If X and Y are independent and respectively, then

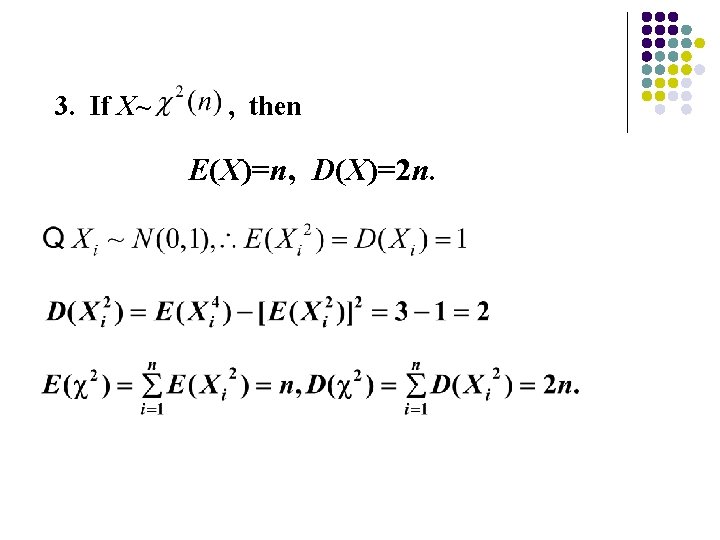
3. If X~ , then E(X)=n, D(X)=2 n.

Definition-α Given , the upper -point of a PDF F is determined from the equation .

Notes: represent the t-value above which we find an area equal to leaves an area of to the right.

Example 1 Assume be a sample from find Example 6. 3 -P 109.

6. 3. 2 t-Distribution Theorem 6. 6 Let X ~N(0, 1)，Y~ . If X and Y are independent, then the distribution of the random variable T, where is given by the density function This is known as the t-distribution with freedom. denoted by degrees of

Notes: 1. represent the t-value above which we find an area equal to leaves an area of 2. 3. to the right.

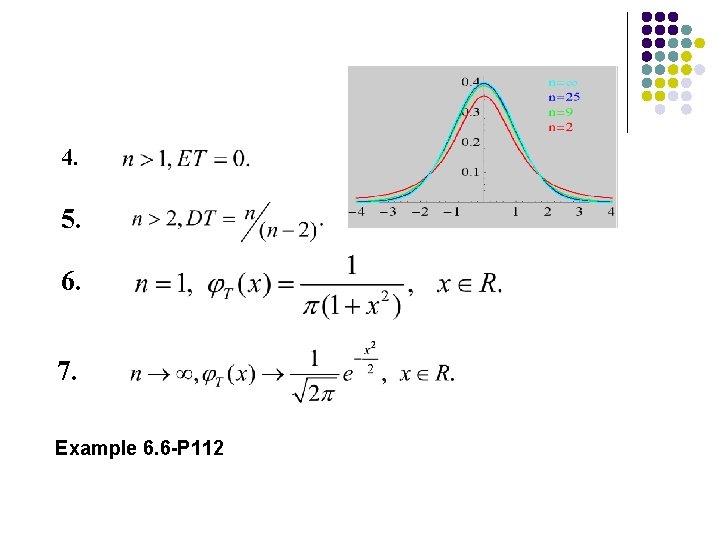
4. 5. 6. 7. Example 6. 6 -P 112

6. 3. 3 F-Distribution Theorem 6. 7 Then the distribution of the random variable is given by the density This is known as the F-distribution with degrees of freedom. Denoted by and

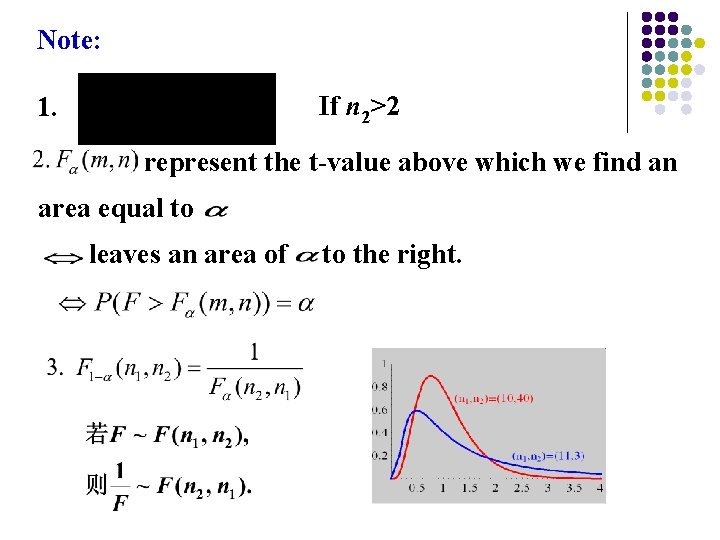
Note: If n 2>2 1. represent the t-value above which we find an area equal to leaves an area of to the right.

6. 3. 5 Theorem 6. 9 -P 117 Let then (1) (2) be a sample from

Theorem 6. 10 -P 118 Let sample mean be a sample from and sample variance with then

Theorem 6. 11 Let be a sample from sample mean and sample variance (1) (2) (3) and are independent. with then

Example Assume a sample of size n=21 from is given, find.

Theorem 6. 12 -P 118 Theorem 6. 14 -P 119

Theorem 6. 13 be independent Let and random samples, respectively, from and distributions, Then. .

Theorem 6. 16 -P 120 be independent Let and random samples, respectively, from and the distributions, Then.

Example Let be a sample from Find the distribution of .

Homework: P 123: 5, 9, 11